Основные законы вращательного движения

 Уравнение (закон) динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси

или

( - момент инерции тела относительно оси z; ε –угловое ускорение)

 Закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т.е. не изменяется с течением времени.

Общие законы поступательного и вращательного движения

 ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ: полная механическая энергия системы тел остается неизменной при любых движениях тел системы

 ОБЩЕФИЗИЧЕСКИЙ ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ: энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой.

1.3 ЭЛЕМЕНТЫ МЕХАНИКИ ТВЕРДОГО ТЕЛА

МОМЕНТ ИНЕРЦИИ ТЕЛА относительно оси – физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси

Момент инерции тела при вращательном движении играет такую же роль, как масса при поступательном движении.

ТЕОРЕМА Штейнера (используется для определения момента инерции твердого тела относительно произвольной оси):

момент инерции тела относительно любой оси вращения равен моменту его инерции относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы тела m на квадрат расстояния а между осями

О d С

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ВРАЩАЮЩЕГОСЯ ТЕЛА представляет собой алгебраическую сумму кинетических энергий отдельных его точек, т.е.

В случае, если тело движется поступательно со скоростью v и одновременно вращается вокруг некоторой оси с угловой скоростью (например, катящееся колесо), то полная кинетическая энергия этого равна

Моменты инерции однородных тел правильной формы

Тонкое однородное кольцо R- радиус; М-масса		(1)
Круглая однородная пластинка - диск R- радиус; М-масса		(2)
Цилиндр R- радиус; М-масса		(3)
Кольцо R и r – соответствующие радиусы; М – масса кольца		(4)
Стержень L- длина стержня; М – масса стержня		(5) (ось проходит через конец стержня) (6) (ось проходит через центр стержня)

§ 1.4 МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ

КОЛЕБАНИЯ - движения или процессы, повторяющиеся во времени.

Простейшим типом колебаний являются гармонические колебания.

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ - колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса.

УРАВНЕНИЕ гармонических колебаний

,

где А – амплитуда - максимальное значение колеблющейся величины;

- фаза колебаний в момент времени t;

- начальная фаза колебаний в момент времени t=0, [φ]=рад;

- круговая (циклическая) частота – число полных колебаний, выраженных в радианной (угловой) мере, за 1 секунду.

[рад/с]

СКОРОСТЬ колеблющейся точки

[м/с]

УСКОРЕНИЕ колеблющейся точки

[м/с²]

ПЕРИОД колебаний – промежуток времени, за который совершается одно полное колебание и фаза колебания получает приращение :

[с]

ЧАСТОТА колебаний – число полных колебаний за 1 секунду (величина, обратная периоду колебаний):

[с^-1=Гц]

СИЛА, действующая на колеблющуюся точку

[Н]

КИНЕТИЧЕСКАЯ энергия

ПОТЕНЦИАЛЬНАЯ энергия

,

ПОЛНАЯ энергия

ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР – система, совершающая колебания, описываемые уравнением:

, решение которого имеет вид:

;

Классические осцилляторы – физический маятник, математический маятник, пружинный маятник.

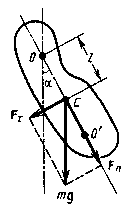
ФИЗИЧЕСКИЙ МАЯТНИК – твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси О подвеса, не проходящей через центр масс С тела.

J – момент инерции маятника относительно оси, проходящей через точку О; - расстояние между точкой подвеса и центром масс маятника; Период колебаний физического маятника Частота колебаний: Циклическая частота:

Приведенная длина физического маятника - длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника (Т_ф=Т_м)

Точка на продолжении прямой ОС, отстоящая от оси подвеса на расстоянии приведенной длины L, называется центром качания физического маятника.

Оборотный маятник – один из типов физического маятника.

Частным случаем физического является математический маятник, вся масса которого сосредоточена в одной точке – центре масс.

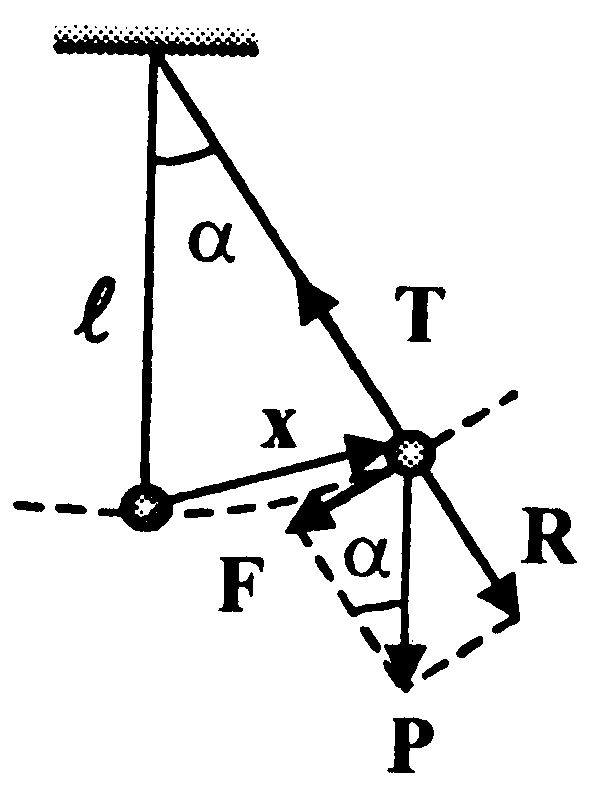
МАТЕМАТИЧЕСКИЙ МАЯТНИК – идеализированная система, состоящая из материальной точки m, подвешенной на нерастяжимой, невесомой нити, и колеблющейся под действием силы тяжести.

Период колебаний математического маятника Частота колебаний: Циклическая частота:

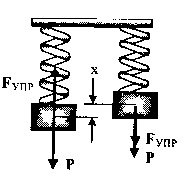
ПРУЖИННЫЙ МАЯТНИК – груз массой m, подвешенный на абсолютно упругой пружине и совершающей гармонические колебания под действием упругой силы , где k – коэффициент жесткости пружины.

Период колебаний пружинного маятника: Частота колебаний: Циклическая частота: