1)Чому оптичне волокно, виготовлене з ізотропного діелектрика, стає анізотропним середовищем для світла, що в ньому розповсюджується?

2)Знайти товщину відсічки ТЕ₃ оптичної моди що розповсюджується в планарному хвилеводі з параметрами: n_f=2.2, n_s=1.9, n_c=1.0, =1.3 мкм.

3)Яка перевага (і чому) градієнтного багатомодового волокна перед ступінчатим багатомодовим.

4)Чому при повному внутрішньому відбитті фаза відбитого променя змінюється в межах (0 – π) в залежності від кута падіння і чому це не має місця при докритичних кутах падіння.

5)Показати, що в неоднорідній плоскій хвилі завжди є повздовжня компонента електричного , або магнітного полей (або обох одночасно).

6) Чому по оптичному хвилеводу неможлива пряма передача зображення?

7)Побудувати амплітудний електрооптичний модулятор світла на подвійній частоті інформаційного сигналу в кристалі LiNbO₃. Електричне поле прикладене вздовж оптичної осі.

8)Оцінити інформаційні можливості одномодового волокна.

9)В якому діапазоні товщин буде підтримуватись одномодовий режим?

10)На яку глибину зануриться оптична мода?

11) Чим відрізняється ТЕ0 від ТЕ5?

12) . Миттєве та середнє за період значення густини потоку енергії ТЕ мод в напрямку сталої розповсюдження.

13) . Миттєве та середнє за період значення густини потоку енергії ТЕ мод в напрямку ортогональному до сталої розповсюдження.

14)Зсув фаз між власними хвилями в електрооптичному кристалі на НВЧ частотах.

15) Чому світло в оболонці і в хвилеводі розповсюджується з однією швидкістю?

16)Оцінити інф. Можливості багатоходового хв.. Знайти W_max на довжині 1км.

17) Принцип действия оптического изолятора

18) Довести, що при ПВВ в області перетину встановиться стояча хвиля.

19)Побудувати фазовий електрооптичний модулятор на частоті сигналу.

20)Розрахувати призм енний елемент.

21)Показати, що n_p>n_f.

22)На якій частоті ак. Сигналу має місце дифракція назад?

23)Розрахувати ефективний діаметр модового поля в хвилеводі на заданій довжині хвилі.

1)Чому оптичне волокно, виготовлене з ізотропного діелектрика, стає анізотропним середовищем для світла, що в ньому розповсюджується?

Тому, що при утворенні трьох шарової структури волокна з трьох анізотропних шарів ( покрівельний шар, хвилеводний шар, підкладинка) виникає ефект природного двозаломлення між ТЕ та ТМ власними модами, що проявляється у різниці між ефективними коефіцієнтами заломлення , де . Причиною появи цього ефектру є різні граничні умови для даних мод, що викликають різні коефіцієнти відбиття від границі і відповідно різні фазові зсуви при відбитті.

2)Знайти товщину відсічки ТЕ₃ оптичної моди що розповсюджується в планарному хвилеводі з параметрами: n_f=2.2, n_s=1.9, n_c=1.0, =1.3 мкм.

Розв’язання

Дисперсійне рівняння для ТЕ_m– хвилеводних мод має вигляд (вивід цього рівняння див. лекції Гайдая ст.31):

(1)

Для кожної пари ортогональних мод (конкретне m) існує своя товщина відсічки (різницею в товщинах відсічки для мод одного порядку можна знехтувати). Визначимо ці товщини, для чого необхідно в рівнянні (1), наприклад, покласти N_m=n_s. Отримаємо:

(2)

З (2) отримуємо:

(3)

Числове значення:

Відповідь:

3)Яка перевага (і чому) градієнтного багатомодового волокна перед ступінчатим багатомодовим.

Інформаційні можливості багатомодового ступінчатого хвилеводу вкрай обмежені внаслідок великої міжмодової дисперсії. Для боротьби з цим явищем розробляють волокна не із ступінчатою зміною показника заломлення, а – градієнтною. В такому волокні основна мода, що розповсюджується по осі хвилеводу є найбільш повільною, оскільки в центрі серцевини найбільша величина показника заломлення. Найбільш швидка мода тепер реалізується при . Наявність градієнту показника заломлення призводить до того, що міжмодова дисперсія не накопичується з відстанню, а в деякому перерізі волокна компенсується до нуля і далі картина періодично повторюється.

Ступінчате волокно:

, де (*Примітка: у чисельнику різниця квадратів!!!*)

Градієнтне волокно:

Обрахуємо смуги пропускання для обох типів волокна.

Відношення ширин смуг пропускання

Видно, що використання градієнтного волокна призводить до зменшення розмиття сигналу за рахунок міжродової дисперсії та до збільшення смуги пропускання каналу зв’язку.

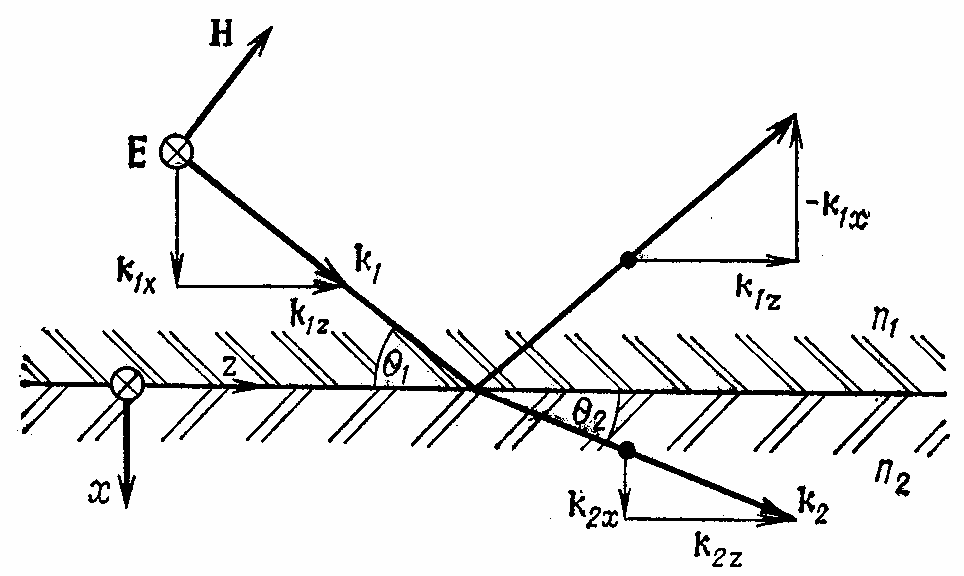
4)Чому при повному внутрішньому відбитті фаза відбитого променя змінюється в межах (0 – π) в залежності від кута падіння і чому це не має місця при докритичних кутах падіння.

Рис. 1

Випадок звичайного відбиття та заломлення показано на рис. 1 (для ТЕ-хвиль).

Падаюча оптична хвиля

; ; ;

Визначимо k₁ = n₁k, k₂ = n₂ k , де - в системі Сі.

Відбита оптична хвиля розповсюджується в тому ж середовищі, що й падаюча, тому квадрат хвилевого вектора тут буде такий само, що і для падаючої хвилі:

; ;

Оптична хвиля, що пройшла. Для оптичної хвилі, що пройшла в області 2 хвилевий вектор відповідає умові:

; ;

Рис. 2

З умови того, що залежність від Z падаючої, та хвилі, що пройшла мають бути однаковими випливає фундаментальний закон геометричної оптики

, або , – а це закон Снеліуса.

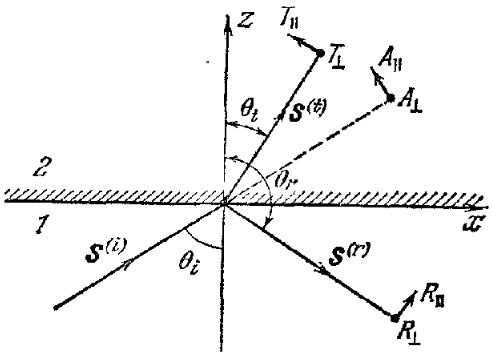
Розглянемо складові електричного та магнітного полів падаючої хвилі (рис. 2). Нехай амплітуда електричного вектора – А. Розкладемо його на складові паралельно та перпендикулярно площині падіння

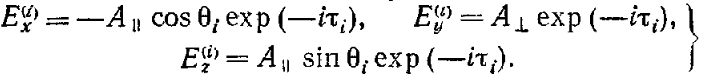
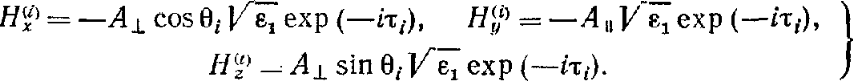
де

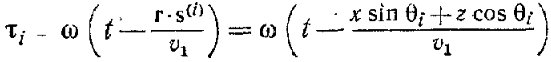
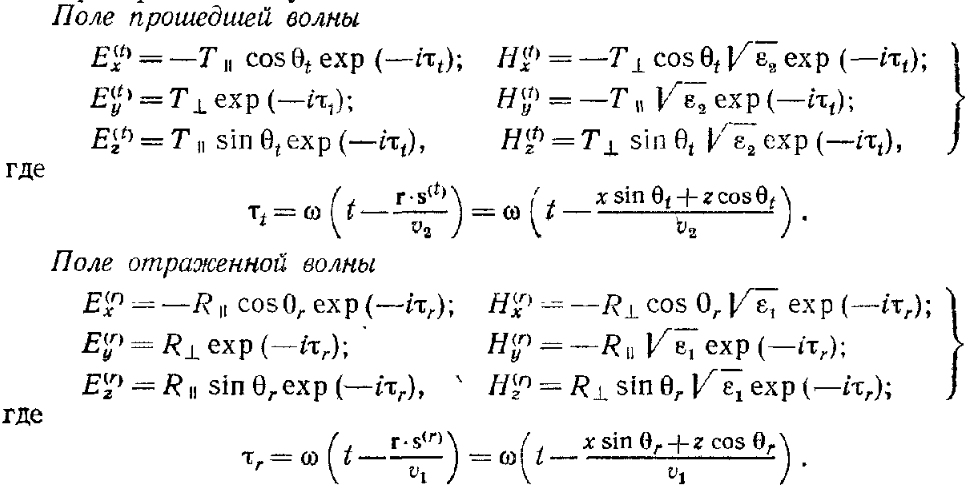
Граничні умови стверджують, що необхідно виконання умови рівності тангенціальних компонент полів

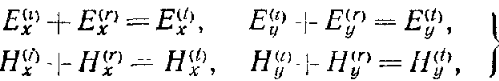
Підставимо поля в граничні умови та використаємо те, що , отримаємо

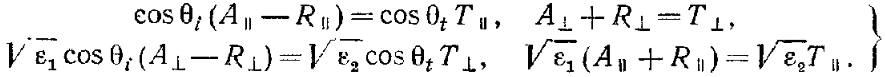
Розвяжемо систему рівнянь, виразивши компоненти відбитих та заломлених хвиль через падаючі

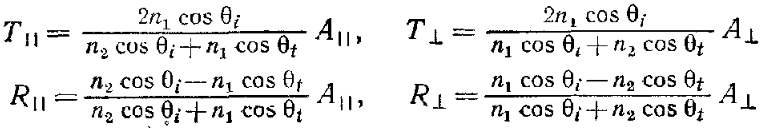
Це і є формули Френеля. У формалізмі рис. 1 та з використанням закону снеліуса отримаємо коефіцієнт відбиття та проходження для ТЕ хвилі:

;

Аналогічно для ТМ хвиль коефіцієнти відбиття та проходження визначаються виразами: ; .

Як бачимо при звичайному відбитті коеф відбиття та заломлення дійсні, а тому не вносять ніяких фазових зсувів.

У випадку ПВВ для якого критичний кут , що випливає з закону снеліуса при .

Як в другому так і в першому середовищах при будь-яких умовах виконується закон збереження квадрату хвилевого вектора:

Починаючи з , і . При < , >

Таким чином, при всіх кутах <

<0

Отже, починаючи з поперечна складова хвилевого вектора у другому середовищі стає уявною. Коефіцієнти відбиття при цьому мають одиничну амплітуду як і при , але стають комплексними з фазовими кутами та .

Виразимо через по закону Снелліуса: , таким чином (вибиремо знак + з огляду фізичних міркувань). Отже коефіцієнт відбиття ТЕ хвиль при повному внутрішньому відбитті стає комплексним:

.

Запишемо це комплексне число в показниковій формі і отримаємо фазовий зсув, що відбувається при ПВВ . Аналогічно одержимо фазовий кут для ТМ хвилі: . (на графіку аргумент половинчастий)