5. Угорський алгоритм

З доказу теореми 1 безпосередньо випливає, що для побудови максимального паросполучення можна застосовувати алгоритм Форда  Фалкерсона. Розглянемо нижче інший шлях рішення цієї задачі, відомий за назвою угорського алгоритму. (Егевари, 1931 р.).

Визначення. Нехай  простий граф і деяке його паросполучення. Дуги назвемо «жирними», інші дуги, «тонкими».

Визначення. Вершину графа назвемо насиченою, якщо вона інцидентна жирній дузі, у противному випадку  ненасиченою.

Визначення. Паросполучення назвемо повною, якщо кожна тонка дуга інцидентна хоча б одній насиченій вершині.

Визначення. Ланцюг, що з'єднує дві ненасичені вершини й складається з тонких і жирних дуг, що йдуть по черзі, назвемо ланцюгом, що чергується.

Рис. 11.3

На мал. 11.3 ланцюгом, що чергується, є, наприклад, ланцюг, якщо - жирні дуги.

Угорський алгоритм полягає в наступному.

Крок 1. Побудувати довільне повне паросполучення .

Крок 2. Якщо відображає всю множину в , то воно максимальне, алгоритм закінчений. Якщо ні, то перейти до кроку 3.

Крок 3. Знайти в графі із установленим у ньому паросполучення довільний ланцюг, що чергується, . Якщо такого ланцюга немає, то максимально, алгоритм закінчений. Якщо такий ланцюг є, то побудувати паросполучення  паросполучення містить всі жирні дуги паросполучення , що не входять у ланцюг і всі тонкі дуги ланцюга (див мал. 11.3 й 11.4). Перейти до кроку 2, поклавши .

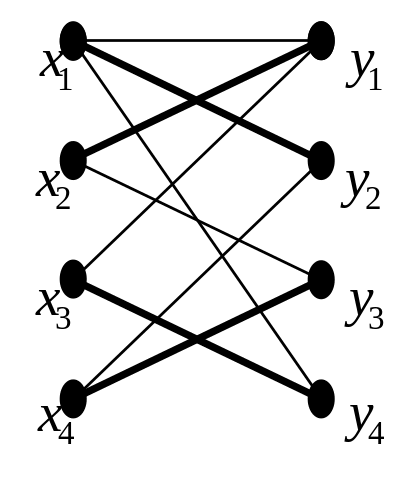
Рис. 11.4

є паросполученням  це випливає з того, що включені в нього дуги ланцюга, що чергується, попарно несуміжні між собою й несуміжні з жирними дугами , що не належать .

Так як число тонких дуг з ланцюга, що чергується, на 1 більше числа жирних, то . Таким чином, кожен перехід від паросполучення до паросполучення на кроці 3 збільшує кількість дуг. Залишається показати, що відсутність ланцюгів, що чергуються, означає максимальність паросполучення. Це буде зроблено пізніше в теоремі 6.

Для пошуку ланцюгів, що чергуються, на кроці 3 побудуємо допоміжний граф . Його вершини відповідають дугам паросполучення й однаково з ними позначаються. З вершини графа у вершину йде дуга, якщо в графі початок дуги суміжний з кінцем дуги .( зокрема, у кожній вершині є петля). Для мал. 11.3 граф зображений на мал. 11.5.

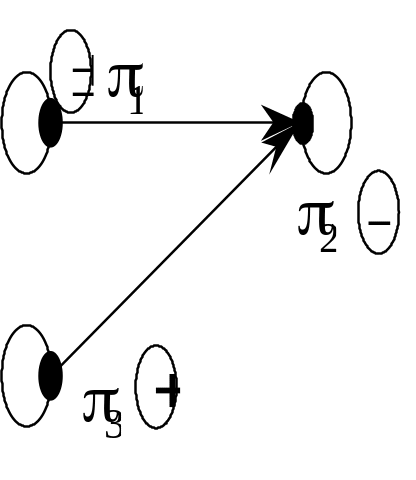
Рис. 11.5

Позначимо через множину тих жирних дуг графа , кінці яких суміжні хоча б з однією його ненасиченою вершиною, а через  множина жирних дуг, початок яких суміжний хоча б з однією ненасиченою вершиною. Наприклад, для графа на мал. 11.3 маємо . У загальному випадку .

Кожному шляху на графі від вершини, що належить множині , до вершини, що належить множині , відповідає ланцюг, що чергується, у вихідному графі. Дійсно, нехай у графі є шлях , у якому , а . Тоді в графі кінець жирної дуги суміжний з деякою ненасиченою вершиною , її початок з кінцем жирної дуги й т.д., початок жирної дуги суміжно з деякою ненасиченою вершиною . Таким чином, вершини й з'єднані ланцюгом, що чергується. Наприклад, шляхи на мал. 11.5 відповідає ланцюг, що чергується, на мал. 11.1.