МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ХАРКІВСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ РАДІОЕЛЕКТРОНІКИ

Лекція 11

Тема: " Паросполучення і трансверсалі. Угорський алгоритм "

Дисципліна: "Дискретна математика"

Викладач Гусарова І.Г.

Харків,2014

ЗМІСТ

1. Поняття паросполучення

2. Теорема про весілля

3. Системи різних представників

4. Дефіцит простого графа

5. Угорський алгоритм

6. Обгрунтування угорського алгоритму

7. Внутрішньо стійкі множини простого графа

8. Питання для самоконтролю

1. Поняття паросполучення

Визначення. Орієнтований граф без кратних дуг називається простим або дводольними (двочастковим), якщо множину всіх його вершин можна представити у вигляді об'єднання двох множин (часток) і так, щоб дуги виходили тільки з вершин множини й заходили тільки у вершини множини .

Такий граф будемо позначати . Приклад простого графа показаний на мал. 11.1.

Рис. 11.1

Визначення. Паросполученням простого графа називається така підмножина множини його дуг, у якому ніякі дві дуги з несуміжні (тобто не мають загальної вершини).

На мал. 11.1 паросполученнями є, наприклад, підмножина дуг і т.д.

Паросполучення ставить у відповідність кожній вершині деякої підмножини одну й тільки одну вершину деякої підмножини . Говорять також, що паросполучення відображає підмножину на підмножину або відображає в .

Наведений приклад показує, що в простому графі можна виділити, як правило, декілька паросполучень. Задача полягає в тім, щоб для даного простого підграфу вказати найбільше паросполучення, тобто таке, котре містить найбільше число дуг, зокрема виділити, якщо це можливо, паросполучення, що відображає все в . До цього зводиться, наприклад, задача про призначення.

В керуванні трудових резервів є працівників , що мають різні спеціальності. Потрібно їх призначити на робочих місць . Деякі із працівників мають (або можуть досить швидко придбати) не одну спеціальність. Чи можна їх розподілити так, щоб кожен працівник зайняв робоче місце у відповідності зі своєю спеціальністю? Цій задачі відповідає двочастковий граф, у якого з вершини у вершину йде дуга, якщо працівник має спеціальність .

Інша популярна форма цієї задачі полягає в наступному. Є деяка множина юнаків, кожний з яких дружить із декількома дівчатами. Запитується, при яких умовах кожний з них може женитися на одній з дівчат, з якими він дружить? Завдяки цій формі, з легкої руки Г. Вейля, теорему про паросполучення, що відображає всю множину в , називають теоремою Кенига  Холу про весілля.

2. Теорема про весілля

Теорема 1. Паросполучення простого графа , що відображає все в , існує тоді й тільки тоді, коли для будь-якої підмножини (нагадаємо, що позначає множину всіх вершин графа , у які заходять дуги, що виходять із вершин множини ,  позначає кількість вершин множини ).

Доведення.

1. Необхідність. Покажемо спочатку, що умова

(11.1)

необхідна. Нехай існує паросполучення , що відображає всю множину в . Тому що ніякі дуги з не суміжні, то нерівність (11.1) повинна виконуватися для кожного .

2. Достатність. Побудуємо допоміжну транспортну мережу (див. мал. 11.2), яка визначена точками множини и , входом і виходом . Мережа містить дугу тоді й тільки тоді, коли в графі є дуга . Пропускні здатності всіх дуг мережі вважаємо рівним . Крім того, мережа містить дуги , що йдуть із входу в усі вершини , і дуги , що йдуть із всіх вершин у вихід. Пропускні здатності цих дуг думаємо рівними 1.

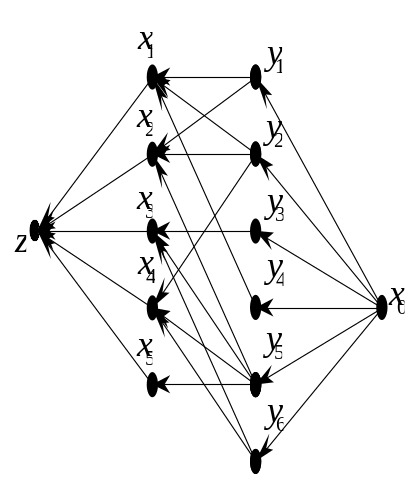
Рис. 11.2

Усякий потік по мережі визначає деяке паросполучення графа . Паросполучення утворюють дуги графа , що відповідають дугам мережі , на яких потік дорівнює 1. Це випливає з того, що з кожної вершини виходить (і в кожну вершину заходить) не більш, ніж одна така дуга. Потоку по мережі , що насичує всі вихідні дуги, відповідає паросполученню, що відображає все в .

Отже, залишається довести, що, якщо для будь-якої підмножини виконується (11.1), то мережа задовольняє умові теореми про насичення.

Нехай  довільна множина проміжних вершин мережі й . По побудові мережі повна потреба множини дорівнює .

Для множини є дві можливості:

1) ;

2) .

У першому випадку пропускна здатність множини задовольняє нерівності . Звідси в силу (11.1) і рівності слідує, що . У другому випадку , тому що в заходить хоча б одна дуга, пропускна здатність якої дорівнює . Отже, і в цьому випадку . Таким чином, умова теореми про насичення для мережі виконана.