НОУ ВПО "БАЛТИЙСКИЙ ИНСТИТУТ ЭКОНОМИКИ

И ФИНАНСОВ" (БИЭФ)

Н.П. Зубарева

Высшая математика

Методическое пособие по изучению темы

"Производная функции и ее применение"

Калининград, 2008

ББК 22.1

Составитель: Н.П. Зубарева, канд. пед. наук, доцент.

Рецензент: А.М. Карлов, доктор техн. наук, профессор.

Методическое пособие предназначено студентам для изучения принципов дифференцирования функций. Подробно пояснено решение отдельных заданий. Для самостоятельного решения предложен ряд заданий, ответы на которые есть на с. 23. В пособии имеется справочный материал.

Печатается по решению Ученого совета БИЭФ, протокол №6 от 03 июля 2008 г.

 БИЭФ, 2008.

 Зубарева Н.П., 2008.

Содержание

Формулы дифференцирования 3

Действия со степенями 4

Уравнение касательной и нормали к кривой 11

Механический смысл производной 12

Приращение функции. Дифференциал функции 13

Исследование функций и построение графиков 15

Ответы 22

Формулы дифференцирования

I. С – постоянная. II. .

III. . IV. .

V. , С – постоянная. VI. .

VII. .

Основные элементарные Сложные функции

функции

VIII. , 8.

IX. , 9. .

X. , 10. .

XI. , 11. .

XII. , 12. .

, 13. .

XIII. , 14. .

XIV. , 15. .

XV. , 16. .

XVI. , 17. .

XVII. , 18. .

XVIII. , 19. .

XIX. , 20. .

XX. , 21. .

Задание 1. Найти производную функции .

Решение:

Функция равна произведению постоянной величины 5 и переменной х². По формуле V выносим постоянную величину перед производной, затем по формуле Х находим производную х².

Задание 2. Найти производную функции .

Решение:

Использовали формулы III, V, II, X.

Найти самостоятельно производную функции:

1а)

1б)

Для вычисления производных полезно сначала преобразовать выражение.

Напомним некоторые формулы действий со степенями.

Действия со степенями

А. . При возведении степени в степень показатели степеней перемножаются.

Б. .

В. . Если основания степеней одинаковы, то при умножении показатели степеней складываются, при делении – показатели степеней вычитаются.

Г.

Д.

Е.

Например:

.

.

.

.

.

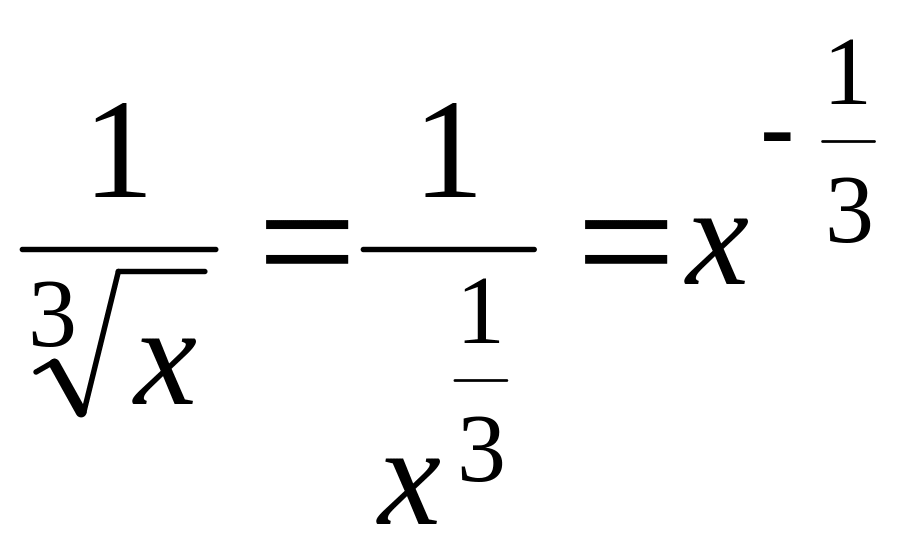Задание 3. Найти производную функции .

Решение: Сначала преобразуем по формуле Е:

.

Производную этой функции найдем по формуле Х:

.

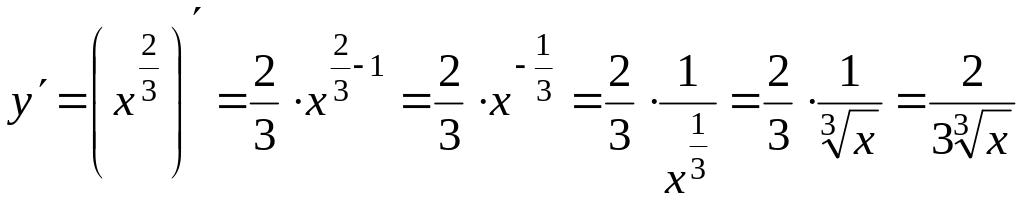Задание 4. Найти производную функции .

Решение: Сначала преобразуем это выражение по формулам Е, Д, Б:

.

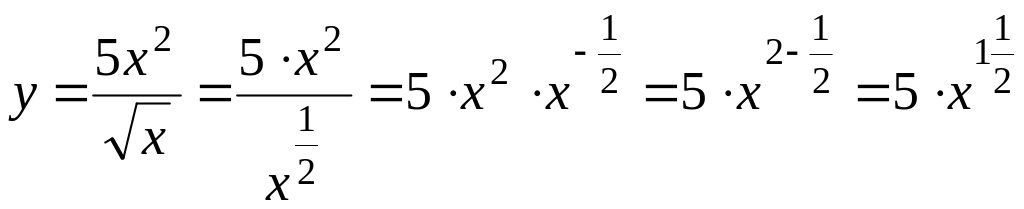Производную этой функции найдем по формулам V, Х:

.

Производную этого выражения можно найти по формуле VI, а потом преобразовать:

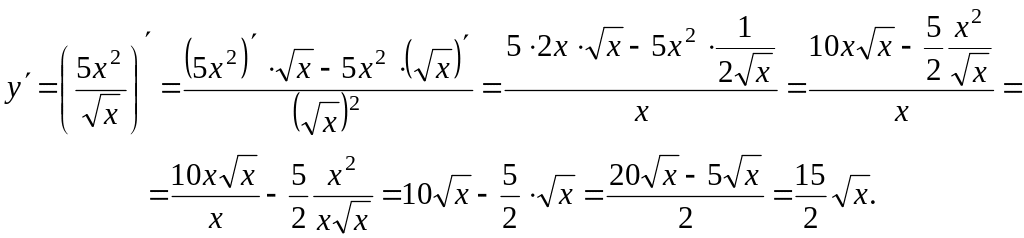
Задание 5. Найти производную функции .

Решение:

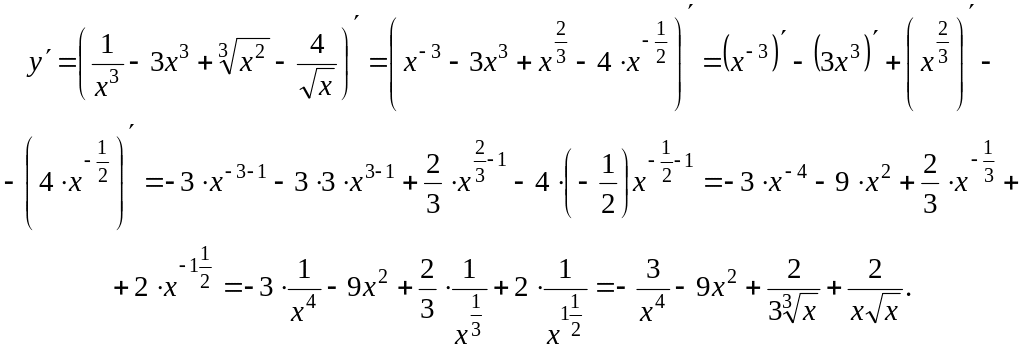
Сначала преобразовали выражение по формулам Д, Е. Производную вычисляли по формулам III, II, X, затем преобразовали полученное выражение по формулам Д, Е.

Найти самостоятельно производную функции:

2а)

2б)

Задание 6. Найти производную функции .

Решение:

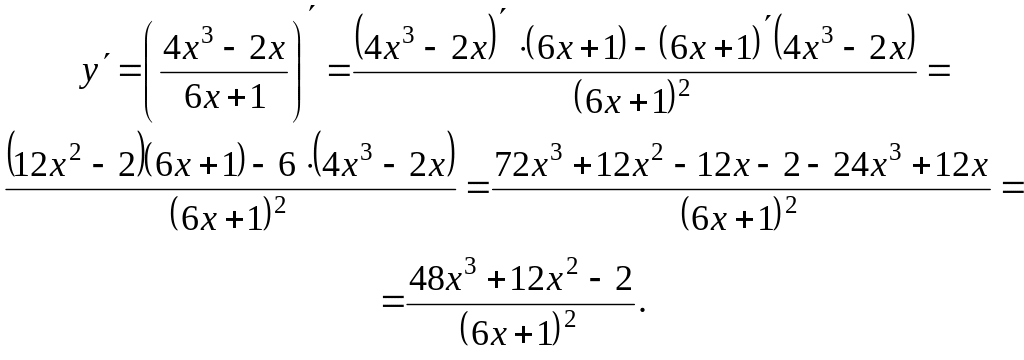
Применили формулу VI. Далее производные находим по формулам III, X, II, I.

Найти самостоятельно производную функции:

3а)

3б)

Задание 7. Найти производную функции .

Решение:

Использовали формулу 10, затем формулы III, V, X.

Найти самостоятельно производную функции:

4а) .

4а) .

Задание 8. Найти производную функции .

Подставим это выражение в виде степени:

.

Производную найдем сначала по формуле 10.

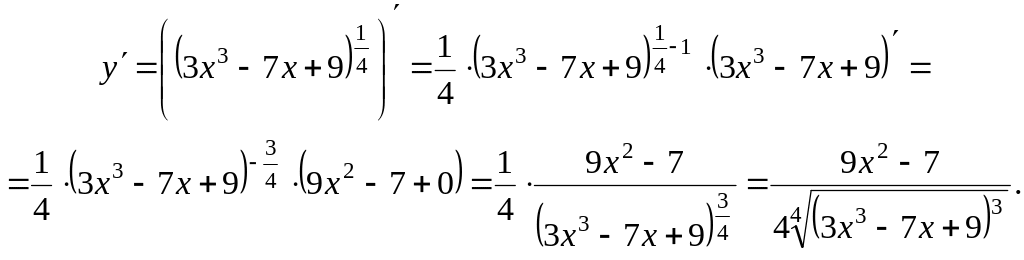
Затем производную находим по формулам III, V, I, X.

Найти самостоятельно производную функции:

5а) .

5б) .

Задание 9. Найти производную функции .

Решение: формула 13, затем формулы III, V, I, X.

Найти самостоятельно производную функции:

6а) .

6б) .

Задание 10. Найти производную функции .

Решение:

формула 12, затем решаем по формулам 11, III, V, I, X.

Найти самостоятельно производную функции:

7а) .

7б) .

Напомним некоторые формулы действий с логарифмическими функциями:

.

.

.

.

.

Эти формулы верны для любого основания логарифмов.

е ≈ 2, 718.

Задание 11. Найти производную функции .

Решение:

формула 8.

Найти самостоятельно производную функции:

8а) .

8б) .

Задание 12. Найти производную функции .

Решение: сначала можно преобразовать по формуле логарифма степени:

.

.

Найти самостоятельно производную функции:

9а) .

9б) .

Задание 13. Найти производную функции .

Решение: - формула 14, V.

Найти самостоятельно производную функции:

10а) .

10б) .

Задание 14. Найти производную функции .

Решение:

(формулы (V, 10, 14).

Найти самостоятельно производную функции:

11а) .

11б) .

Задание 15. Найти производную функции .

Решение: (формулы V, 10, 16).

Найти самостоятельно производную функции:

12а) .

12б) .

Задание 16. Найти производную функции .

Решение:

(формулы IV, XIII, XIV).

Найти самостоятельно производную функции:

13а) .

13б) .

Задание 17. Найти производную функции .

Решение:

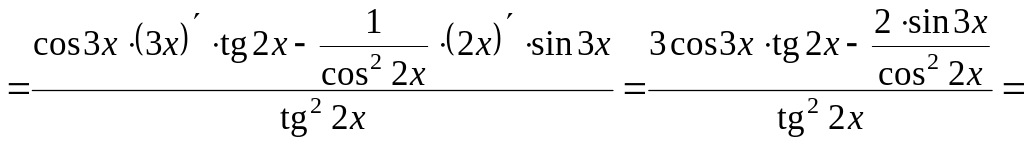
(формулы VI, 14, 16, V).

Найти самостоятельно производную функции:

14а) .

14б) .

Задание 18. Найти производную функции .

Решение: 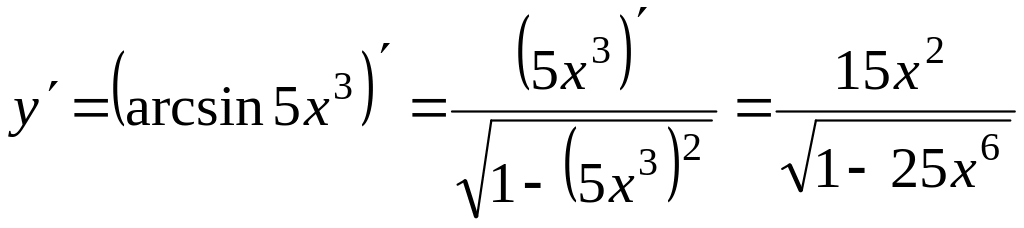(формула 18).

Найти самостоятельно производную функции:

15а) .

15б) .

Задание 19. Найти производную функции .

Решение: (формула 20).

Найти самостоятельно производную функции:

16а) .

16б) .

Задание 20. Найти производную функции .

Решение: Используя формулу , получим .

Найти самостоятельно производную функции:

17а) .

17б) .

Задание 21. Продифференцировать функцию .

Решение: (формулы 12, XIII).

Найти самостоятельно производную функции:

18а) .

18б) .

Производную от данной функции часто называют первой производной (или производной первого порядка). От производной также можно взять производную, которую называют второй производной (или производной второго порядка) и обозначают .

Производной третьего порядка (или третьей производной) называют производную от второй производной. Её обозначают .

Например, для функции имеем .