РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ
ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ
Мартиросовой Юлии Александровны
Зачетная книжка №ХХХХХХХХ
ФТТС
курс
Группа №5
2014 г.
Задача 1
Необходимо 3 контейнера разместить в 2 складах. Сколькими способами это можно сделать?
Решение
В данной задаче я использовала комбинацию - сочетание без повторений.
Сочетаниями
из
элементов по
элементов
называются соединения, каждое из
которых состоит из
элементов, взятых из данных
элементов. Эти соединения отличаются
друг от друга хотя бы одним элементом.
В отличие от размещений, порядок
следования элементов здесь не учитывается.
Число
сочетаний из
элементов
по
элементов обозначается символом
и
вычисляется
по формуле:
.
Я использую сочетание без повторений т.к. :
Контейнера в комбинациях участвуют по одному разу и не повторяются
В каждой новой комбинации состав контейнеров в складах меняется
Порядок размещения контейнеров в складах не важен (т.е. , например, комбинации 123 и 321 считаются одинаковыми)
Таким образом, количество способов размещения 3 контейнеров в 2 складах:
=
= 3.
Задача 2
В ящике находится 9 деталей. Из них 3 бракованных. Наугад из ящика взяли 4 детали. Какова вероятность того, что:
А) все взятые детали окажутся качественными?
Б) ровно 3 детали окажутся качественными?
В) менее 2 деталей окажутся качественными?
Решение
Вероятность (Р) - это отношение числа благоприятных исходов(m) ко всем возможным исходам(n).
Р=
А) Поскольку для нас благоприятный исход - все 4 взятые детали качественные (всего в ящике 6 качественных деталей) , а все возможные исходы – 4 любые детали взятые из 9, то вычислим вероятность, используя сочетания (т.к. нам не важен порядок в комбинациях из деталей) :
Р(А)=
=
=
=
= 0.1190476
Б) Благоприятный исход – ровно 3 из взятых 4 деталей качественные (всего качественных 6), соответственно 1 деталь бракованная (всего бракованных 3). Все возможные исходы - 4 любые детали взятые из 9. Вероятность вычислим используя сочетания и правило умножения(т.к. из 4 выбранных деталей 3 качественные И(!) 1 бракованная).
Правило
умножения (основной
принцип): если
из некоторого конечного множества
первый объект (элемент
)
можно
выбрать
способами и после каждого такого
выбора второй объект (элемент
)
можно
выбрать
способами,
то оба объекта (
и
)
в
указанном порядке можно выбрать
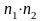способами.
Р(Б)=
=
=
=
= 0.4761904
В) Благоприятный исход – 1 деталь будет качественной и 3 бракованные. Все возможные исходы - 4 любые детали взятые из 9. Вероятность вычислим используя сочетания и правило умножения(т.к. из 4 выбранных деталей 1 качественная И(!) 3 бракованные):
Р(В)=
=
=
=
= 0.047619
Задача 3
Набирая номер телефона, абонент забыл последние 2 цифры и набрал их наугад. Найти вероятность того, что он дозвонился, если:
А) он знает, что все цифры не повторяются.
Б) он знает, что все цифры совпадают.
В) он не имел никакой дополнительной информации.
Решение
Всего есть 10 цифр(0,1,2,3,4,5,6,7,8,9).
А) Благоприятный исход здесь один – правильный набор последних цифр (m=1). Всех возможных исходов здесь будет столько, сколько можно составить комбинаций из 2 цифр, порядок которых имеет значение, значит вычисляем вероятность с помощью размещений.
Размещениями из элементов по элементов называются соединения, каждое из которых состоит из элементов, взятых из данных элементов. При этом размещения отличаются друг от друга как самими элементами, так и их порядком.
Число
размещений из
элементов
по
элементов обозначается символом
и
вычисляется
по формуле:
,
где
,
.
Вероятность того, что абонент дозвонился, если он знает, что все цифры не повторяются:
P(A)=
=
Б) Аналогично условию А), благоприятный исход здесь один – правильный набор последних цифр (m=1). Всех возможных исходов здесь будет столько, сколько можно составить комбинаций из 2 цифр, порядок которых имеет значение, НО которые при этом совпадают, значит вычисляем вероятность с помощью размещений с повторениями:
P(Б)=
=
В) Если абонент не имел никакой дополнительной информации, то набранные 2 цифры могут быть ИЛИ разные, ИЛИ одинаковые (события несовместны). Тогда вероятность суммы двух событий равняется сумме двух вероятностей(согласно теореме сложения вероятностей).
Получаем:
P(A+Б)=Р(А)+Р(Б)=
