ОБРАЗЕЦ ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ

Задание 1

Методом Крамера найти решение системы линейных алгебраических уравнений

.

Решение.

Решение системы находим по формулам Крамера

.

Вычислим определитель системы

.

Последовательно заменив в , первый, второй и третий столбцы столбцом свободных членов, получим соответственно

;

;

.

Ответ : .

Задание 2.

Вычислить произведение матриц: и .

Решение.

= .

Задание 3.

Исследовать данную систему уравнений 3а совместность и решив ее, если она совместна:

Решение.

Для этой системы уравнений составим ее матрицу А и расширенную матрицу A1.

Система будет совместной, если ранг ее матрицы будет равен рангу ее расширенной матрицы, т. е.

Найдем ранги данных матриц:

Отсюда следует, что , т.е. система совместна. Найдем решение данной системы. Из последней матрицы выпишем систему уравнений:

Ответ:

Задание 4.

Представить заданную систему линейных алгебраических уравнений в матричной форме и решить ее с помощью обратной матрицы. Пользуясь правилом умножения матриц, показать, что произведение матрицы системы на обратную матрицу равно единичной матрице Е.

Решение.

Запишем данную систему в Матричной форме: ,где

, ,

Для решения системы воспользуемся следующей формулой : , но прежде выясним, имеет ли матрица обратную матрицу . Найдем определитель системы:

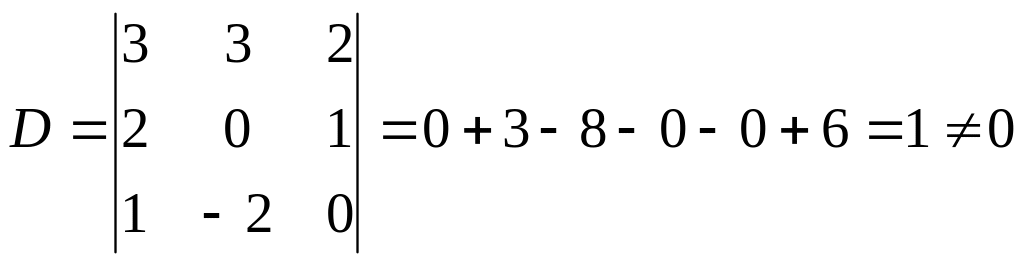
а это означает, что матрица существует:

Вычислим алгебраические дополнения по формуле: .

Тогда

Итак, решение системы: .

Покажем, что произведение матрицы системы на обратную ей матрицу равно единичной матрице Е.

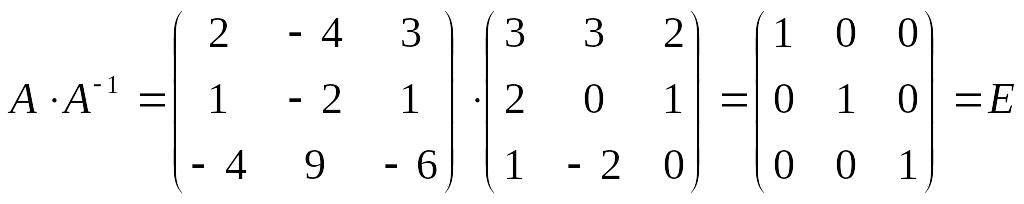
Ответ:

Задание 5.

Даны векторы . Показать, что векторы образуют базис трехмерного пространства, найти координаты вектора в этом базисе

Решение.

Покажем, что векторы линейно независимы. Вычислим определитель, составленный из координат этих векторов:

значит, векторы линейно независимы и образуют базис трехмерного пространства.

Поскольку векторы образуют базис трехмерного пространства, то вектор можно единственным образом разложить по данному базису:

, где – координаты вектора в базисе .

,

отсюда

.

Решая данную систему мы получаем .

Т. об., разложение вектора по базису имеет вид .

Ответ: .

Задание 6.

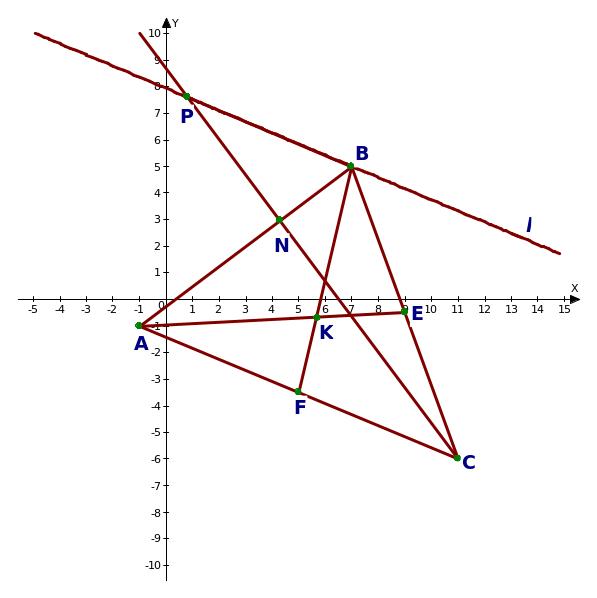
Даны вершины треугольника АВС. Требуется найти:

1.длины сторон АВ и АС, их уравнения и угловые коэффициенты;

2.величину угла А в градусах до двух знаков после запятой;

3.точку пересечения медиан треугольника АВС;

4.уравнение высоты СN и её длину;

5.уравнение прямой l, проходящей через вершину В параллельно стороне АС;

6.площадь треугольника АВС;

7.сделать чертёж.

А(-1;-1) B(7;5) C(11;-6)

Решение:

1.Длина стороны АВ и АС находится как расстояние между двумя точками по формуле:

(1)

Для нахождения уравнений сторон АВ и АС воспользуемся уравнением прямой, проходящей через две точки:

(2)

Подставляя в (2) координаты точек А и В, получаем уравнение стороны АВ:

Разрешив последнее уравнение относительно , находим уравнение стороны АВ в виде уравнения прямой с угловым коэффициентом:

Подставляя в (2) координаты точек А и С, получаем уравнение стороны АС:

Разрешив последнее уравнение относительно , находим уравнение стороны АВ в виде прямой с угловым коэффициентом:

2. Известно, что тангенс угла между двумя прямыми, угловые коэффициенты которых соответственно равны и , вычисляется по формуле:

(3)

Искомый угол А образован прямыми АВ и АС, угловые коэффициенты которых найдены в пункте 1):

Применяя (3), получаем:

Используя таблицу Брадиса, получаем что:

3. Точку К пересечения медиан треугольника АВС найдем, решив совместно систему уравнений любых двух медиан треугольника. Для этого найдем уравнения медиан АЕ и ВF, проведенных из вершин А и В.

Сначала найдем координаты точки Е, которая является серединой стороны ВС ,затем точки F, которая является серединой стороны АС, применяя формулы деления отрезка пополам:

(4)

Подставим в (4) координаты точек В и С , получим координаты точки Е:

Подставим в (4) координаты точек А и С, получим координаты точки F:

Подставив в (2) координаты точек А и Е, получим уравнение прямой (медианы) АЕ:

Подставив в (2) координаты точек В и F, получим уравнение прямой (медианы) BF:

Чтобы найти координаты точки К, пересечения медиан AE и BF, решим совместно систему уравнений:

Умножим оба уравнения системы на 2, получим:

Решим данную систему методом Крамера.

4. Уравнение прямой, проходящей через данную точку в заданном направлении, имеет вид:

(5)

Высота CN AB. В данном случае ( ) –координаты точки С (11,-6). Чтобы найти угловой коэффициент высоты CN, воспользуемся условием перпендикулярности прямых: если прямая то т.к. . Подставим в уравнение (5) координаты точки С и найдем угловой коэффициент высоты CN, получаем:

/

Координаты точки N пересечения высоты CN со стороной АВ найдем, решив совместно систему, составленную из уравнений этих прямых:

Решим данную систему методом Крамера.

5.Пусть искомая прямая .Тогда по условию , а согласно условию параллельности двух прямых

Подставляя в (5) координаты точки В, получаем уравнение:

/

Чтобы найти координаты точки P пересечения прямой с высотой CN ,решим совместно систему уравнений:

Решим данную систему методом Крамера.

Р(0,8;7,6)

6.Вычислим площадь треугольника АВС, пользуясь понятием определителя, т.е. формулой:

кв.ед.

7.Сделаем чертеж.