2 Графоаналітичний метод спектрального аналізу періодичних сигналів

Спектральний аналіз (Spectral analysis, синоніми: Фур'є аналіз, гармонійний аналіз, Frequency analysis) - це різновид обробки даних, пов'язаний з перетворенням їхнього частотного подання або спектра. Спектр виходить у результаті розкладання вихідної функції, що залежить від часу (часовий ряд) або просторових координат (наприклад, зображення), у базис деякої періодичної функції. Найбільш часто для спектральної обробки використовується спектр Фур'є, який одержують на основі базису синуса (розкладання Фур'є, перетворення Фур'є).

Основний зміст перетворення Фур'є в тому, що вихідна неперіодична функція довільної форми, яку неможливо описати аналітично й у загальному випадку важка для обробки та аналізу, представляється у вигляді сукупності синусів або косинусів з різною частотою і амплітудою. Іншими словами, складна функція перетвориться в множину більш простих. Кожна синусоїда (або косинусоїда) з певною частотою і амплітудою, отримана в результаті розкладання Фур'є, називається спектральною складовою або гармонікою. Спектральні складові створюють спектр Фур'є.

Спектром сигналу називається сукупність гармонійних коливань, з яких складається сам сигнал.

Якщо говорити більш точно, то існує два основні типи спектрів: амплітудно-частотний (амплітудний) і фазочастотний (фазовий) спектр.

Амплітудним спектром називається розподіл амплітуд гармонійних складових по частоті.

Фазовим спектром називається розподіл початкових фаз гармонійних складових по частоті.

Оскільки основна частина енергії імпульсу зосереджена в області головної пелюстки, то за ширину спектру береться ширина головної пелюстки.

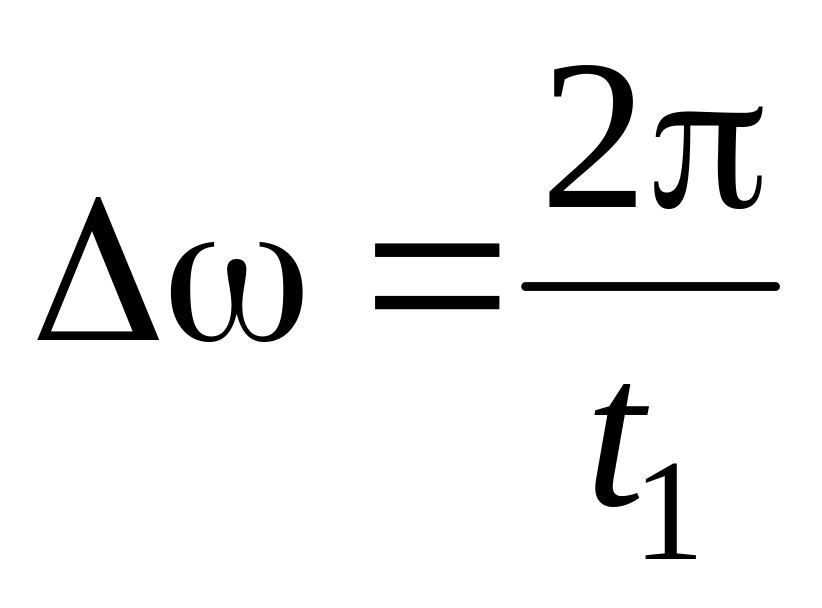,	(2.1)
де 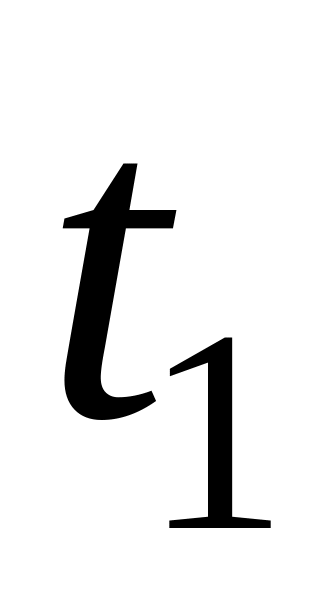- тривалість імпульсу.

π

π

π

Рисунок 2.1 - Амплітудний спектр

Теоретично спектр тягнеться до нескінченності.

Рисунок 2.2 - Фазовий спектр

Сутність графоаналітичного методу полягає у визначенні спектральних складових (гармонік) сигналу на основі його окремих дискретних значень (вибірок), узятих через обрані проміжки часу.

Порядок розрахунків

1. Період сигналу, заданого графіком, розбити на М однакових проміжків, попередньо вибравши початок системи координат.

2. Виписати значення сигналу (орти) , і розрахувати збільшення фази на дискретний проміжок часу

.

Записати в загальному виді ряд Фур'є з урахуванням обраної системи координат.

3. Розрахувати коефіцієнти ряду, використовуючи наступні формули, отримані шляхом заміни інтегральних виражень наближеними сумами:

	(2.5)
	(2.6)
	(2.7)

4. Розрахувати амплітуди й початкові фази гармонік (косинусоїд) тригонометричного ряду Фур'є через

(2.8)

де амплітуда -ої гармоніки;

початкова фаза -ної гармоніки;

2.1 Спектральне представлення сигналів

Окрім звичного тимчасового (координатного) представлення сигналів і функцій при аналізі і обробці даних широко використовується опис сигналів функціями частоти, тобто по аргументах, зворотних аргументах тимчасової (координатної) вистави. Можливість такого опису визначається тим, що будь-який скільки завгодно складний по своїй формі сигнал можна представити у вигляді суми простіших сигналів, і, зокрема, у вигляді суми простих гармонійних коливань, сукупність яких називається частотним спектром сигналу.

Математично спектр сигналів описується функціями значень амплітуд і початкових фаз гармонійних коливань по безперервному або дискретному аргументу - частоті. Спектр амплітуд зазвичай називається амплітудно-частотною характеристикою (АЧХ) сигналу, спектр фазових кутів - фазочастотною характеристикою (ФЧХ). Опис частотного спектру відображує сигнал так само однозначно, як і координатний опис.

Рисунок 2.3 - Часове представлення сигналу

Як приклад на рисунку 2.3 приведений відрізок сигнальної функції, яка отримана підсумовуванням постійної складової (частота постійної складової дорівнює 0) і трьох гармонійних коливань. Математичний опис сигналу визначається формулою

,

(2.9)

де - амплітуда коливань;

- частота коливань в герцах;

- початковий фазовий кут коливань в радіанах; .

Частотне представлення даного сигналу (спектр сигналу у вигляді АЧХ і ФЧХ) приведене на рисунку 2.4. Звернемо увагу, що частотне представлення періодичного сигналу , обмеженого по числу гармонік спектру, складає всього вісім відліків і вельми компактно в порівнянні з неперервним часовим представленням, визначеним в інтервалі від до .

Рисунок 2.4 -Частотне представлення сигналу