6.3.7 Основні поняття і рівняння гідродинаміки

Сили, прикладені до будь-якого виділеного об’єму рідини, обмежену замкнутою поверхнею, підрозділяють на дві групи – масові (об’ємні) і поверхневі.

Масовими називають сили, віднесені до одиниці маси або об’єму рідини, наприклад сила інерції або тяжіння. Поверхневими називають сили, які прикладені до одиниці поверхні, що обмежує даний об’єм рідини, наприклад тиск, сила тертя. Поверхневі сили можна представити у вигляді нормальної і дотичної напруги, прикладеної на поверхні об’єму рідини. У ідеальній рідині сили тертя відсутні, отже, поверхневі сили будуть представлені тиском. В цьому випадку основна властивість гідростатичного тиску – незалежність його від напряму – буде справедливо і в гідродинамічних умовах. Це означа­є, що тиски в трьох взаємно перпендикулярних площинах, проходячих че­рез дану точку (рис. 6.13, а), рівні між собою: рх=рy=рz=р. При сталій течії рідини або газу зміни маси в даному об’ємі не відбувається, що означає рівність об’ємів втекаючої і витікаючої рідини.

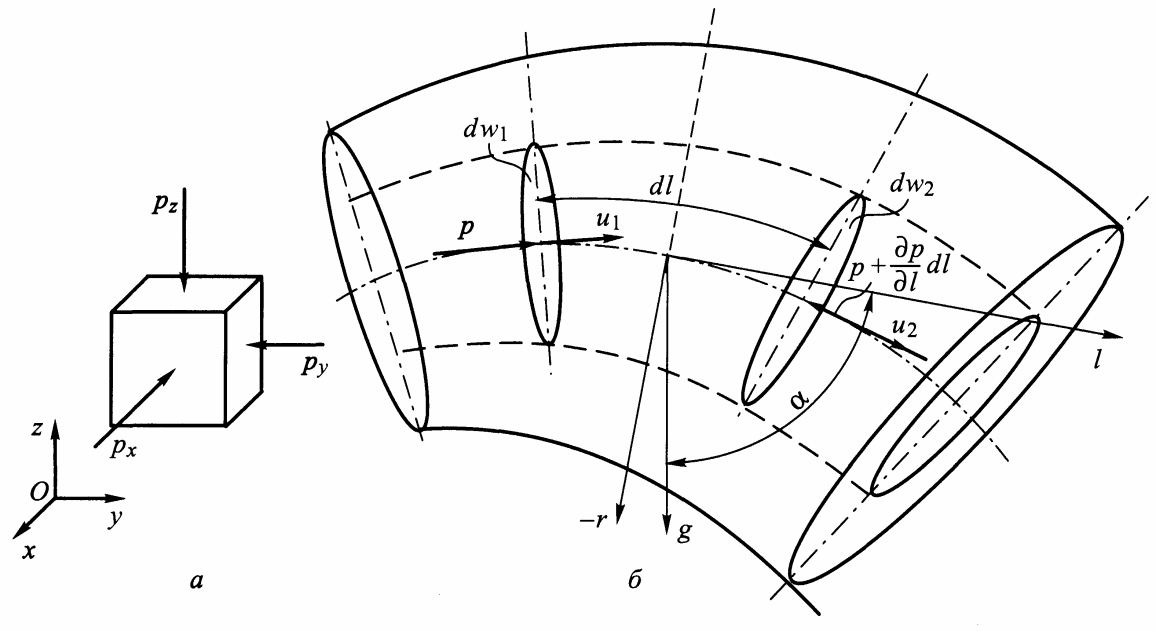
Рисунок 6.13 – Трубка дотику і елементарна струмина

Вивчення потоку рідини в трубопроводі показало, що її частки, розташовані поблизу осі, рухаються з великими швидкостями, чим частки, які знаходяться в стінках. При розгляді гідродинамічних явищ виділяють елементарну струмину, розміри поперечного перетину якої нескінченно малі, а значить, швидкість її течії можна прийняти постійною. Для визначення поня­ття елементарної струмини додатково вводять поняття лінії і трубки дотику.

Під лінією струму в потоці розуміють лінію, дотична до якої в кожній точці збігаються з напрямом вектора швидкості. Для сталого руху лінія струму завжди збігається з траєкторією часток рухомої рідини, розташованих на ній. При несталому русі частки рідини на лінії дотику знаходяться одну мить.

Трубкою дотику називають трубчасту поверхню замкнутого нескінченно ма­лого контура, створюючими якого є лінії струму. Рідину, заповнюючи трубку дотику, утворює елементарну струмину (рис. 6.13, б).

Потік можна розглядати як сукупність елементарних струминок. Переріз трубки дотику dω, перпендикулярне її створювачу, називають живим. У сталому потоці форма елементарних струмин постійна, а в неусталеному – безперервно змінюється. При вивченні елементарної струмини рівняння Ейлера записують в так званій природній формі. Координатними осей в цьому випадку будуть дотична, головна нормаль і бінормаль до лінії струму, причому проекції сил, що діють, на бінормаль дорівнюють нулю. Позначаючи напрям дотичної до лінії дотику через l (рис. 6.13, б), а головною норма­лю через r і складаючи суми проекцій сил, що діють, отримуємо:

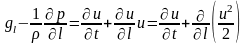     (6.8)

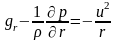                        (6.9)

де r – радіус кривизни лінії дотику, м.

В даному випадку маємо два рівняння з трьома невідомими (u, p, ρ), для вирішення яких необхідне додаткове рівняння. Таким є рівняння нерозривності, для виведення якого в природній формі розглянемо нескінченно малий відрізок dl довжини елементарної струмини (рис. 6.13, б), обмеженою перетинами dω₁ і dω₂ (рис. 6.13, б). Якщо масова витрата рідини через перетин dω₁ позначить як (ρdQ)₁, то масова витрата (ρdQ)₂ через переріз dω₂ із умови нерозривності струмини буде мати вид:

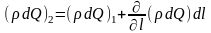        (6.10)

У загальному випадку:

    (6.11)

Зміна маси може статися лише в результаті зміни густини ρ і об’єму елементарної струмини. Секундний приріст маси можна визначити по формулі:

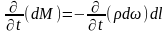                   (6.12)

З виразів (6.11) і (6.12) маємо:

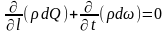             (6.13)

У загальному випадку 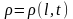, , 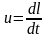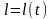. Отже:

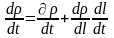                        (6.14)

Продиференціювавши рівняння (6.13) і підставивши 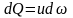, і з (6.14), після перетворень отримаємо:

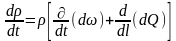         (6.15)

Рівняння (6.13) і (6.15) є рівняннями нерозривності в натуральній формі. Нехай має місце стала течії: 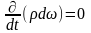. Тоді, згідно рівнянню (6.13):

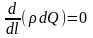                    (6.16)

Або

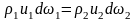                 (6.17)

В разі несталого руху рідини при постійній густині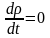 . Тоді рівняння нерозривності (6.15) набере вигляду:

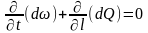             (6.18)

Гідродинамічні рівняння Ейлера в природній формі (6.9) для скраплинної рідини можна проінтегрувати і задачу гідродинаміки вирішити з врахуванням рівняння нерозривності. Згідно рис. 6.13, можна записати:

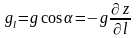                (6.19)

З врахуванням g_l друге рівняння (6.9) можна представити у вигляді:

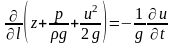          (6.20)

Рівняння (6.20) є рівняння Бернуллі в диференціальній формі, яке можна інтегрувати по довжині елементарної струмини:

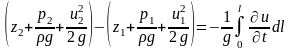(6.21)

Для несталого руху рівняння Бернуллі справедливе лише для двох часток ідеальної рідини, що знаходяться на одній лінії струму в розглядуючий момент часу. При сталому русі воно справедли­во також і для однієї і тієї ж частки рідини, що знаходиться в двох положе­ннях на траєкторії, бо остання збігається з лінією дотику.

Розглядаючи елементарну струмину реальної рідини, необхідно враховувати гідродинамічні втрати, обумовлені зростаючими при перебігу силами тертя між окремими шарами рідини. Рівняння Бернуллі для реальної рідини можна записати у вигляді:

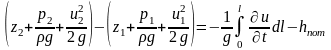(6.22)

де h_пот – гідродинамічні втрати між двома перетинами елементарної струмини рідини.