1.3 Теорія подібності крильчастих насосів

1.3.1 Явище подібності у відцентрових насосів

При конструюванні динамічних машин широко використовують моделювання, тобто випробування їх на моделях, які геометрично подібні промисловому зразку, але відрізняються від нього зменшеними розмірами. Досліди на моделі дозволяють перевірити якість машини і з найменшими затратами в лабораторних умовах відпрацювати елементи конструкції. Формули подібності забезпечують перехід від характеристики моделі до характеристики натури і навпаки.

Допустимо насоси "н" (натура) і "м" (модель) подібні. Умови геометричної подібності цих машин полягають у рівності однойменних кутів і постійності відношень однойменних геометричних величин, тобто _1н=_1м=₁; _2н=_2м=₂:

(1.28)

де  – коефіцієнт геометричної подібності.

Геометрична подібність моделі і натури повинна поширюватися не тільки на всі основні розміри конструкції але і на шорсткість поверхонь проточної частини машини. Але підібрати шорсткість поверхонь натури і моделі так, щоб відношення їх дорівнювало коефіцієнту  геометричної подібності, практично неможливо.

Кінематична подібність полягає в постійності відношень швидкостей в однойменних точках геометрично подібних машин (подібності трикутників швидкостей):

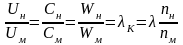(1.29)

де _к – коефіцієнт кінематичної подібності;

 – коефіцієнт геометричної подібності;

n_н і n_м – відповідно частота обертання коліс натурного насоса і його моделі, об/хв.

Динамічна подібність виражається постійністю відношень сил однакової природи, які діють в однойменних точках геометрично і кінематично подібних машин (динамічна подібність виконується при рівності числа Re натури і моделі), тобто:

(1.30)

звідки

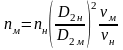(1.31)

У випадку, якщо n_м виходить надмірно великим значенням, то не обов’язково дотримуватись умови Re_м=Re_н. В цьому випадку моделювання відцентрових насосів проводять наближено (за умовами геометричної подібності) і для перерахунку параметрів користуються формулами пропорціональності.

ККД машин, працюючих в подібних режимах, приблизно можна вважати однаковими. При точних розрахунках ККД корегують за дослідними формулами.

1.3.2 Коефіцієнт швидкохідності. Класифікація коліс за коефіцієнтом швидкохідності

Коефіцієнтом швидкохідності насоса n_s називають частоту обертів насоса, подібного даному, який створює напір 1м при корисній потужності 735Вт в режимі максимального ККД.

Коефіцієнт швидкохідності визначається за формулою:

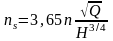(1.31)

де Q – подача насоса, м³/c;

n – частота обертання, об/хв;

Н – напір насоса, м.

n_s визначається для будь-якої динамічної машини на оптимальному режимі її роботи, причому він зберігає своє значення при роботі на в’язких рідинах, тоді як інші параметри оптимального режиму змінюються.

Динамічні насоси класифікують за коефіцієнтом швидкохідності (рис.1.4) наступним чином:

Рисунок 1.4 – Класифікація динамічних насосів за коефіцієнтом швидкохідності

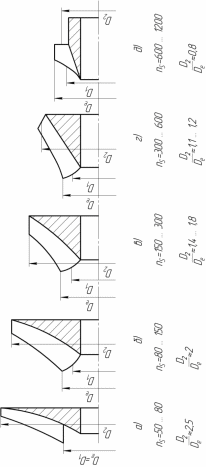
1) вихрові насоси – n_s=10...50; 1,7;

2) тихохідні відцентрові насоси – n_s =50…80; 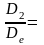2,5;

3) нормальні відцентрові насоси – n_s =80...150; 2;

4) швидкохідні відцентрові насоси – n_s =150...300; 1,8...1,3;

5) відцентрово – осьові – n_s =300...600; 1,2...0,9;

6) осьові – n_s =600...1200; 0,8.

При даних Q і Н і коли n_s n, то із збільшенням частоти обертання зменшуються розміри і маса насоса.

За коефіцієнтом швидкохідності, який визначається за формулою (1.31), можна вибрати тип машини з заданими Q, Н, n.