1.2.4 Залежність подачі, напору і потужності насоса від частоти обертання вала

Подача реального відцентрового насоса визначається залежністю:

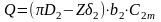(1.14)

де πD₂ – довжина кола на виході робочого колеса, м;

Z ₂ – звуження “живого” перерізу колеса на виході, м;

Z – число лопатей робочого колеса;

₂ – товщина лопаті на виході робочого колеса, м;

b₂ – ширина каналу (лопаті) на виході, м;

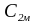– величина меридіональної складової абсолютної швидкості рідини на виході робочого колеса, м/с.

Розглядаючи трикутник швидкостей рідини на виході робочого колеса (рис.1.3) видно, що при зміні частоти обертання вала насоса з n (при якій існували швидкості ) на n₁ отримаємо нові швидкості , які при тих же кутах і 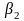утворюють трикутник швидкостей, подібний і пропорціональний першому. Виходячи із подібності трикутників можна записати:

(1.15)

Відомо також, що ,

звідки (1.16)

Зважаючи, що в формулі (1.14) всі величини правої частини рівняння постійні, за виключенням швидкості , яка пропорціональна подачі Q, то підставляючи значення (1.16) у (1.14) отримаємо:

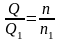(1.17)

тобто подача насоса прямопропорціональна частоті обертання вала.

Рисунок 1.3 – Трикутник швидкостей рідини на виході із робочого колеса

Згідно рівняння Ейлера для безударного режиму роботи насоса .

Оскільки 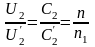, то при зміні частоти обертання вала з величини на величину 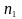, створюваний насосом напір буде:

(1.18)

Отже, напір насоса пропорціональний квадратові частоти обертання вала.

Потужність насоса визначається залежністю:

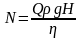(1.19)

При зміні частоти обертання вала з величини n на величину n₁ і враховуючи формули (1.17) і (1.18), отримаємо:

(1.20)

тобто потужність пропорціональна кубові частоти обертання вала насоса.

Залежності (1.17), (1.18), (1.20), при роботі насоса на одній і тій же рідині називаються законами пропорціональності.

1.2.5 Баланс енергії і коефіцієнт корисної дії динамічної машини

Енергія, що підводиться від двигуна до вала динамічної машини, більша корисної енергії, яку отримує рідина чи газ. Це пояснюється тим, що в процесі перетворення енергії у динамічній машині, частина механічної енергії обов’язково втрачається внаслідок гідравлічних і механічних втрат.

Механічні втрати мають місце в підшипниках, ущільненнях а також в результаті тертя рідини в бокові стінки робочого колеса (дискові втрати). Дискові втрати залежать від частоти обертання робочого колеса, густини і в’язкості рідини, розмірів і шорсткості поверхонь робочого колеса і стінок корпуса, а також від витрати рідини. В сучасних відцентрових насосах 80% механічних втрат припадає на дискові втрати. Втрати потужності на тертя в підшипниках залежать від конструкції підшипників, їх мащення, а також від коефіцієнту тертя.

Ущільнення насоса призначене для того, щоб не пропускати повітря в насос (якщо воно працює під вакуумом), чи запобігти втратам рідини із насоса вздовж вала (якщо воно працює під тиском). Ущільнення вала не може бути абсолютно герметичним так як необхідні пропуски рідини, достатні для відводу тепла, яке виникає при терті.

Механічні втрати енергії визначаються виразом:

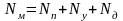(1.21)

де N_п – втрати потужності на підшипниках, Вт;

N_у – втрати потужності в ущільненнях вала, Вт;

N_д – дискові втрати енергії, Вт.

Корисна потужність:

N_к=N–N_м (1.22)

Механічний ККД:

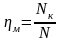(1.23)

де N_к – корисна потужність насоса (потужність, що передається лопатями робочого колеса рідині, Вт;

N – потужність насоса, Вт.

Механічний ККД оцінює досконалість насоса як механізму. В сучасних відцентрових насосах _м =0,92…0,99.

Об’ємні втрати обумовлюються перетоками рідини (газів) через зазори між робочим колесом і корпусом машини із зони підвищеного тиску в порожнину всмоктування. Від потоку, що проходить через робоче колесо машини, відокремлюється частина витрати , яка проходить через зазори на вхід робочого колеса. Якщо ступінь відцентрової машини подає у вихідний патрубок Q, а через зазори циркулює витрата , то через робоче колесо проходить (Q+ ).

Об’ємний ККД:

(1.24)

Величина об’ємного ККД суттєво залежить від величини осьового і радіального зазорів між робочим колесом і корпусом машини. За об’ємним ККД оцінють досконалість машини з точки зору її герметичності. Значення в сучасних відцентрових машинах знаходиться в межах =0,96…0,98.

Гідравлічні втрати виникають в результаті гідравлічного тертя, удару та вихроутворення у всій проточній частині машини і визначаються експериментально. Якщо гідравлічні втрати складають h м, то очевидно, робоче колесо повинно створювати напір (H+h) (де H – напір насоса). Гідравлічні втрати оцінюються за допомогою гідравлічного ККД:

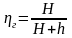(1.25)

На коефіцієнт впливають форма проточної частини машини, шорсткість внутрішніх поверхонь і в’язкість рідини. Значення в сучасних відцентрових машинах знаходиться в межах =0,8…0,96.

Загальний ККД відцентрової машини:

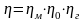(1.26)

В сучасних відцентрових насосах ККД досягає значення 0,92. Співвідношення між різними втратами залежить від форми робочих органів і змінюється на різних режимах роботи насоса.

Потужність двигуна для приводу динамічного насоса:

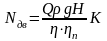(1.27)

де Q – подача насоса, м³/с;

– густина рідини, кг/м³;

H – напір насоса, м;

– ККД насоса;

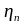– ККД передачі (між двигуном і насосом);

К – коефіцієнт запасу потужності двигуна (К=1,05…1,2). Менше значення приймають для потужних насосів, а більше – для малопотужних насосів.