6.6. Полупроводниковые лазеры [28]

До сих пор нами обсуждались лишь атомарные и молекуляр­ные системы, энергетические уровни которых связаны с лока­лизованными волновыми функциями, т. е. относящимися к от­дельным атомам или молекулам. Рассмотрим теперь полу­проводники, для которых уже нельзя использовать волновую функцию отдельного атома;[вместо этого необходимо иметь дело с волновой функцией, определяемой кристаллом в целом. Ана­логично нельзя более говорить об энергетических уровнях от­дельных атомов. /

Принцип действия полупроводникового лазера можно рассмо­треть с помощью рис. 6.37, на котором показаны валентная зона полупроводника V, зона проводимости С и ширина запрещенной зоны Eg. Если предположить для простоты, что полупроводник Находится при температуре Т= О К, то валентная зона будет полностью заполнена электронами, в то время как зона прово­димости будет пуста (см. рис. 6.37, а, где заштрихованная об­ласть является областью заполненных состояний). Предполо­жим теперь, что электроны каким-либо образом переведены из

валентной зоны в зону проводимости. Внутри этой зоны элек­троны за очень короткое время (~ Ю^-13 с) перейдут на ее

самый нижний уровень, а все электроны вблизи максимума ва­лентной зоны также перейдут на самые нижние из незанятых уровней, так что верхушка валентной зоны будет заполнена «дырками». Отсюда следует, что между валентной зоной и зоной проводимости возникает инверсия населенностей (рис. 6.37,6). Электроны из зоны проводимости сваливаются назад в валент­ную зону (т. е. они рекомбинируют с дырками), испуская при этом фотон (рекомбинациониое излучение). Если между зоной

₁

₁

7Т

₁

V

_4.

_а

Рис. 6.37. Принцип действия полупроводникового лазера.

проводимости и валентной зоной существует инверсия населен­ностей, как показано на рис. 6,37, б, то процесс вынужденного рекомбинационного излучения приведет к генерации при нали­чии подходящего резонатора и выполнении соответствующих по­роговых условий.

Лазерную генерацию на основе вынужденного рекомбина­ционного излучения в полупроводниковых р — я-переходах на­блюдали почти одновременно четыре группы исследователей в 1962 г. [29—32], причем три из них использовали GaAs.

6.6.1. Фотофизические свойства полупроводниковых лазеров

В данном разделе мы напомним некоторые наиболее элемен­тарные результаты теории полупроводников, имеющие непосред­ственное отношение к нашему ' обсуждению. За более подробным

рассмотрением читатель может обратиться к общепринятым учебникам по квантовой механике твердых тел [33].

6.6.1.1. Энергетические состояния

_в

полупроводниках

Волновую функцию электрона в данной зоне, например ва­лентной, можно записать в виде волновой функции Блоха:

_{*r(r) = tf,*(r)e}^,k_-^r_,

(6.24)

_{где Uvk(r) обладает теми же свойствами периодичности, что и}

кристаллическая решетка, а постоянная распространения k свя­зана с импульсом электрона р известным соотношением

р = йк. (6.25)

Для полупроводникового кристалла, имеющего форму прямо­угольного параллелепипеда с размерами L„ Ц и U вектор к квантуется аналогично выражению (2.10), а именно

k_t = 2nl/L_h (6.26)

где / = х, у, г, а / — целое число.

Если блоховскую волновую функцию (6.24) подставить в волновое уравнение Шрёдингера, описывающее движение элек­трона в полупроводнике, то окажется, что разрешенные значе­ния энергии электронов Е —Е (k) попадают в зоны, среди кото­рых заполненная зона называется валентной, а следую­щая, более высокая — зоной проводимости. Появление зонной структуры связано с дифракцией Брэгга блоховской волновой функции на периодическом кристаллическом потенциале. Од­нако существование валентной зоны и зоны проводимости мож­но объяснить с помощью несложных физических соображений. Рассмотрим для простоты случай натрия, в котором каждый атом имеет 1 1 электронов. Десять из них тесно связаны с ядром

и образуют положительный ион зарядом Одиннадцатый

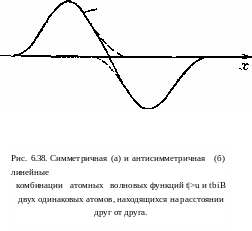
электрон движется по орбите вокруг этого иона. Обозначим энергии этого последнего электрона в основном и первом возбу­жденном состоянии через Е[ и Е₂, а соответствующие волновые функции гЬ 1 и Ф₂. Рассмотрим теперь два атома натрия, располо­женные на некотором расстоянии d. Если d много больше раз­меров атома, то два атома не будут взаимодействовать друг с

^{другом и энергии обоих состояний не изменятся. По другому это}

можно выразить следующим образом. Если рассматривать, на­пример, два атома в их энергетических состояниях Ей то одно-электронный уровень энергии двухатомной системы по-прежне­му равен Ей и этот уровень дважды вырожден. Действительно, полную волновую функцию можно выразить через комбинацию двух волновых функций i|)ia и фц*, причем эти две функции складываются либо в фазе, либо в противофазе (рис. 6.38), В отсутствие потенциала взаимодействия эти два состояния имеют одну и ту же энергию Е\. Однако когда расстояние ме­жду атомами d достаточно мало, энергии этих двух состояний будут слегка различаться: благодаря взаимодействию дважды

^{вырожденный уровень расщепляется на два. Аналогично для}

системы из N атомов, в которой атомы располагаются доста­точно близко друг к другу и взаимодействуют между собой,

jV-кратно вырожденное состояние с энергией Е\ расщепляется на /V близко расположенных уровней. Следовательно, состояние с энергией Е\ приводит к валентной зоне, в то время как со- стояние с энергией Н₂ приводит таким же образом к зоне прово- димости (рис. 6.39). Из предыдущих рассуждений следует, что каждая зона на самом деле состоит из N близко расположен- ных уровней, где N — полное число атомов в кристалле полу- проводника. Поскольку N, d как правило, очень велико»

отдельные уровни энергии полупроводника внутри каж­дой зоны в общем случае не могут быть разрешены.

В пределах каждой зоны разрешенные значения энергии можно связать с соответствующими значениями k выражением, которое в приближении параболической зоны записывается так же, как и в случае свободной частицы. Таким образом, для зоны

^{проводимости имеем}

_{Ес (К) =}

fk*/2fn

(6.27)

где т_с — эффективная масса электрона Аналогично для валентной зоны имеем

_{Ev (k)=*b}²_&l2mv\

в зоне проводимости.

(6.28)

здесь масса электрона в валентной

зоне. Заметим, что энергия £ отсчитывается от дна зоны прово­димости в случае Е_с и от верхушки валентной зоны в случае E_v.

На рис. 6.40 построены кривые разрешенных значений £ в за­висимости от вычисленных по формулам (6.26)-(6.28). На рисунке эти значения обозначены темными точками в валент­ной зоне и светлыми кружками в зоне проводимости. Заметим, что, согласно выражению (6.26), разрешенные состояния разде­лены по оси k равными проме­жутками 2ж/Ь. Заметим также, что ситуация, изображенная на рис. 6.40, соответствует прямозон-ному полупроводнику, в котором минимум зоны проводимости и

^{максимум валентной зоны}

дятся на одну и ту же точку в пространстве волновых векто­ров k

6.6.1.2. Заполнение уровней при тепловом равновесии

Поскольку в соответствии с выражением (6.24) волновая функция электрона распростра­няется на весь кристалл, можно применить принцип Паули, со­гласно которому каждый уровень энергии может "быть занят не бо­лее чем двумя электронами. Со­ответственно вероятность запол­нения f(E) данного состояния с энергией Е (в валентной зоне

или зоне проводимости) дается статистикой Ферми - Дирака, а не статистикой Максвелла - Больцмана. Таким образом.

/(£) = {!+ ехр l(E-E_f)IkT]}

-1

_(6.29)

где Ef — энергия так называемого уровня Ферми Этот уро­вень имеет следующий физический смысл: когда Т + имеем

f = I при Е < E_f, f — 0 при Е > Е_{.

(6.30)

Таким образом, этот уровень представляет собой границу ме­жду полностью заполненными и пустыми уровнями при Т = 0 К.

Здесь для простоты не рассматривается упомянутое выше двукратное вырождение каждого уровня по спину электрона. — Прим. перев.

В невырожденных полупроводниках уровень Ферми распола­гается внутри запрещенной зоны (рис. 6.40). Таким образом, при Т = 0 К валентная зона будет заполнена полностью, а зона проводимости будет пустой. Можно показать, что в этих усло­виях кристалл не проводит, т. е. является изолятором. Заметим также, что уровень Ферми имеет также и другое свойство — при любой температуре f(Ef) — 1/2.