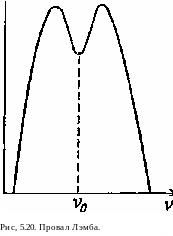
5.3.8. Провал Лэмба и активная стабилизация

^{частоты лазера}

Другое интересное явление, которое нельзя объяснить в рам- ках используемого здесь приближения скоростных уравнений, представляет собой провал Лэмба, названный так в честь фи- зика У. Э. Лэмба, который предсказал его теоретически [20]. _ 1 Это явление имеет место в любых

"Т газовых лазерах, работающих на

одной моде, если преобладает неод­нородное уширение, обусловленное эффектом Доплера. Провал Лэмба иллюстрируется на рис. 5.20, где приведена зависимость выходной мощности от частоты генерации при постоянной скорости накачки. Кри-

Зеркало 2

Рис. 5.21. Насыщение усиления в газовом лазере с доплеровски уширенным перехо­дом.

вая такой формы может быть получена экспериментально в одно-модовом лазере, частота выходного излучения которого пере­страивается посредством плавного изменения длины резонатора

(на величину, равную половине длины волны). Как видно из рис. 5.20, кривая выходной мощности имеет провал на централь­ной частоте перехода, что на первый взгляд кажется парадок­сальным.

Чтобы объяснить такую зависимость мощности от частоты, рассмотрим экспериментальную ситуацию, показанную на рис. 5*21, когда насыщение в активной среде, вызванное полем лазерного излучения, регистрируется пробным пучком малой интенсивности (т. е. ненасыщающим), который распространяет­ся под небольшим углом к оси резонатора (ср. с рис. 2.15). Нач­нем рассмотрение со случая, когда частота генерации лазера

vsjfcvo (например, v<v₀). Лазерное излучение будет взаимо­действовать только с теми атомами, направление скорости v ко­торых противоположно по отношению к направлению излуче­ния, а ее величина v такова, что v[l+(t»A)]=v₀ (эффект Доплера). Однако в резонаторе лазера волна распространяется между зеркалами как в прямом, так и в обратном направлении. Следовательно, волна, распространяющаяся вправо, будет вза­имодействовать с атомами, движущимися плево, в то время как волна, распространяющаяся влево, взаимодействует с атомами,

Контур

- доплероВтй линии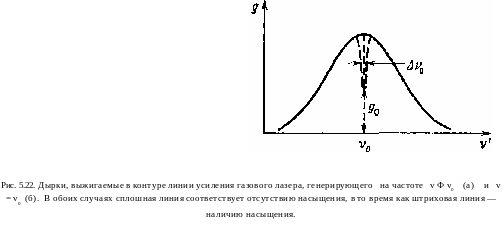

движущимися вправо. Таким образом, рассматриваемая мода будет приводить к насыщению населенности двух групп атомов: одних, движущихся со скоростью -\-v, и других, движущихся со скоростью —v. При этом, как было показано в разд. 2.6.3 (см. рис. 2.19), из-за насыщения, обусловленного интенсивным ла­зерным излучением, в линии усиления g(v)_f регистрируемой пробным пучком, образуются две «дырки» при частотах, соот­ветствующих скоростям движения атомов ±v. Следовательно, одна из частот равна v, а другая располагается симметрично к первой относительно v₀ (рис. 5.22,а). Ширина каждой дырки порядка однородной ширины линии. При каждой из этих двух частот кривая насыщенного усиления g(v) дается выражением (2.147). В частности, на частоте v имеем

^{£ = go(v)/[l + /(v)//sb (5.67)}

где go — коэффициент ненасыщенного усиления, а / — интенсив­ность каждой из двух противоположно направленных волн (для простоты предполагается, что они имеют одинаковые интенсив­ности). Если рассмотреть теперь случай, когда v=Vo» то лазер­ное излучение будет взаимодействовать с теми атомами, кото­рыс имеют v =& При этом обе дырки на рис. 5.22, а сливаются в одну, расположенную в центре линии усиления (рис. 5.22,6). В этом случае насыщенное усиление (рис. 5.22,6) g(vo) запи­шется в виде

^{8 Ы = go (v}₀^{)/[ 1 + 2/ (v}₀^{)//,]. (5.68)}

Множитель 2, стоящий в квадратных скобках этого выражения, учитывает то обстоятельство, что обе волны насыщают теперь одну и ту же группу атомов. Следовательно, в данном случае должна быть более глубокая «дырка» (ср. рис. 5,22, а и 5.22,6), это и является фундаментальной причиной появления провала в центре спектра выходной мощности. Действительно, в рассмо­тренных двух случаях выходную мощность можно получить из условия, что насыщенное усиление на длине активной среды g

должно быть равно потерям резонатора у. Поскольку Р = 1АТ₂

(см. рис. 5.21), из выражений (5.67) и (5.68) для обоих случаев находим соответственно [ср. с (5.33) ]

Р (v) = AT₂I_S [g₀ (v)/y - 1 ], (5.69)

. р (v₀) = (1/2) AT₂I_S [g₀ (v₀)/y — 1], (5.70)

где А — площадь поперечного сечения лазерного пучка, а Т₂ — коэффициент пропускания выходного зеркала. Множитель 1/2 в правой части выражения (5.70) означает, что P(v₀)<P(v), и, следовательно, он ответствен за провал Лэмба. Заметим, что, поскольку ширина «дырок» на рис. 5.22 примерно равна одно­родной ширине линии, то ширина провала Лэмба также срав­нима с этой шириной линии.

Явлением провала Лэмба можно воспользоваться для очень эффективной стабилизации частоты лазера [19]. Поскольку ши­рина провала Лэмба примерно равна однородной ширине ли­нии, а в газовых лазерах она обычно много меньше неоднород­ной ширины линии (ср. значения Av_ecT и AvJ, приведенные для

неона в разд. 2.3.3.1 и 2.3.3.2), положение дна лэмбовского про­вала фиксируется с очень высокой степенью точности. Предпо­ложим, что одно из зеркал резонатора укреплено на пьезоэлек­трическом преобразователе таким образом, что длина резонатора

может очень плавно меняться при приложении электрического напряжения к преобразователю. Тогда с помощью соответствую­щего электронного устройства обратной связи частоту лазера можно стабилизировать относительно минимума лэмбовского провала. В Не—Ne-лазере применение такого метода позволило

получить стабильность и воспроизводимость частоты генерации

порядка Ю^-9. Это значение стабильности ограничивается тем,

_{что центральная частота перехода сама по себе не является}

Обращенный. _у провал Лэмба

_{идеально стабильной, поскольку она зависит (хотя и в ма­лой степени) от давления газа и силы тока разряда. Еще луч­шую стабилизацию обеспечивает метод, основанный на исполь­зовании явления, аналогичного провалу Лэмба, который имеет место, когда газ (который не накачивается) с линией поглоще­ния на частоте va в пределах линии усиления лазера помещает­ся в отдельной кювете внутрь резонатора. В соответствии с проведенным выше рассмотрением в этом газе в условиях насы­щения {т. е. в процессе генера­ции лазера) коэффициент погло­щения должен иметь провал, гда частота лазерного излучения v совпадает с va. В этом случае сле­дует ожидать, что выходная мощ­ность лазера будет иметь вместо}

провала узкий пик (часто назы­ваемый обращенным провалом Лэмба) при v=v_a (рис. 5.23). Заметим, что ширина обращен­ного провала Лэмба обычно

меньше ширины провала Лэмба, поскольку через поглотитель не проходит ток, а также потому, что поглотитель можно поддер­живать при более низком давле­НИИ. Таким образом, стабилизи­руя частоту лазера на частоте об-

ращенного провала Лэмба, мож­но достичь лучшей стабильности и воспроизводимости частоты генерации (Д\'_Ген/^_Ген = Ю~¹²—1(Н³). Для Не—Ne-лазера, ге­нерирующего на частоте Я = 3,39 мкм, в качестве поглотителя

применяют газ метан, а при генерации на длине волны к = = 0,633 мкм - 1*4.2. Достижение столь высоких значений моно­хроматичности и стабильности частоты особенно важно для

метрологических применений лазеров (лазерный стандарт ча­стоты).