4.7.2. Резонансные частоты и дифракционные потери

Все, что мы делали до сих пор, относится к вычислению соб­ственных функций распределения поля. Для расчета резонанс­ных частот предположим снова, что и являются 2-К00р-динатами двух зеркал относительно начала координат, рас­положенного в перетяжке пучка. Из продольного фазоВого множителя в (4.95) получаем следующее выражение, из кото­рого можно найти резонансные частоты:

kL — (1 + m + 0 [arctg {zJz_R}- arctg )= ля. (4.127) Действительно, из этого выражения следует, что

_{v =} _f_ {„ + _{(1 + m + /}) ["ctg _nz_r) - arctg _{г_хЫ\ j ^ ^

После некоторых утомительных выкладок последнее выражение можно переписать через параметры резонатора g\ и g₂\

^{V =}"2TL^"^ ^U ~т~^пг~^{т l}} я" J* ^.129)

Заметим, что частотное вырождение, которое наблюдается для конфокального резонатора (рис. 4.29), в обобщенном сфериче­ском резонаторе снимается. В качестве примера, имеющего важ­ное значение, рассмотрим почти плоский резонатор, образован­ный двумя одинаковыми, почти плоскими зеркалами, т. е. слу­чай, когда L/R < 1. При этом arccos(^₂)^1/2 = arccos 11 -— (L/R)] » {2L/R)^1/2и выражение (4.129) принимает вид

^v = Ж [^п + <¹ + ^т + *> Т (Ц) ^т] • (4-130)

Вычисленный по этой формуле спектр частот представлен на рис. 4.36 (ср. с рис. 4.19).

Наконец, перейдем

_к

определению дифракционных потерь,

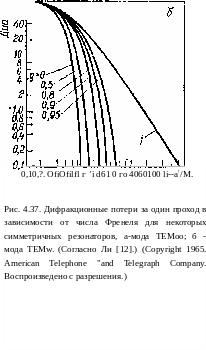Дело в том, что для этого в каждом ходимо решать интегральное урав­нение Френеля - Кирхгофа. На рис. 4.37 приведены как характер­ные и весьма полезные примеры

(п< 1,0,0}

вычисленные зависимости дифрак­ционных потерь от числа Френеля для некоторых симметричных резо­наторов (которые характеризуются соответствующими значениями па­раметра g). Заметим, что для дан-шго числа Френеля наименьшие по­тери имеет конфокальный резона­тор (g = 0).

_{1р. о,о)}

/[(nMlnAlfl

к онкретном случае необ-

а о,/ o,2tit0jsi,o ?. 4 еею го towюо а- воЬ

с/21

Рис. 4.36, Частотный спектр мод симметрич­ного резонатора со сферическими зеркала­ми в случае, когда радиус кривизны зер­кал R много больше длины резонатора I.

4.7.3. Условие устойчивости

^{чек РО и Р, относительно оси резонатора, a r'}_Q ^{и г}

1

рые эти лучи образуют с осью резонатора, тогда в

Получим сначала условие устойчивости с помощью геоме­трической оптики. Обратимся к рис. 4.38 и рассмотрим луч, вы­ходящий из точки Ро, принадлежащей некоторой плоскости р внутри резонатора. После отражения на зеркалах 2 и 1 этот луч пересечет плоскость р в точке Р,. Если го и г; — координаты то­- углы, кото-

_{соответствии}

с (4.5) можно написать следующее соотношение:

		А	В		г0
Л		С	D		г' 'о

(4.131)

да

_i

где ЛВСЯ-матрица — это матрица преобразования лучей, соот­ветствующая полному проходу резонатора. Луч, выходящий из точки /мл, г'Л после двух отражений; пересечет плоскость р

в точке Р₂(г₂» координаты которой определяются выраже­нием

г*		А	В			А	В	2
г'		С	D	Л		С	D

^(4.132)

Таким образом, после п полных проходов луча че­рез резонатор координаты точки Р_п (г_п, г^) запишутся

г г

го г'

^{в виде}

п

п

_{А В} ^п

_{С D}

^{(4.1 33)}

Резонатор будет устойчивым, если при любом выборе исходной точки г'Л точка (г, г') с увеличением п не будет удаляться

на бесконечно большое расстояние от оси. Это означает, что

матрица

А В^п С D

не должна расходиться с увеличением п. Поскольку определи­тель AD — ВС матрицы равен единице, из матричного исчисле­ния [13] получаем

А В" , С D ^smT^X

где

_X

^{A sin лв — sin (п — 1)9 Bsinn9}

С sin пВ D sin nQ — sin (ti — 1) в

cos 8 = (A+D)/2.

(4.134)

(4.135)

Отсюда следует, что для того, чтобы матрица (4.134) не расхо­дилась, должно выполняться неравенство

-1<{A + D)/2<1. (4.136)

В самом деле, если это неравенство не выполняется, то угол в будет комплексным числом и sin пд должен неограниченно уве­личиваться с я.

Чтобы найти условие устойчивости данного резонатора, мы должны теперь определить соответствующую ему АВСО-мят-рицу. Если плоскость р на рис. 4.38 расположить непосредст­венно перед зеркалом 1, то результирующая матрица будет рав­на произведению следующих четырех матриц. Первая из них описывает свободное распространение от зеркала 1 до зеркала 2, вторая — отражение от зеркала 2, третья — свободное рас­пространение от зеркала 2 до зеркала 1 и четвертая — отраже­ние от зеркала I. Тогда из выражения (4.16) получаем

(4.137)

Перемножение матриц дает соотношение

AD 21 2L

R\

(4.138)

которое можно преобразовать к виду

A + D + 2 /. L W, L\

_{4 \}^l_-lb)V-irJ=⁸_*⁸_*

_(4.139)

_{О <С "л ^ 1 >}

_{Поскольку условие (4.136) можно записать в эквивалентном виде как}

_(4.140)

4

1 1

отсюда с учетом соотношения окончательно получаем

очень простое неравенство, выражающее условие устойчивости резонатора:

0<gig₂<l. (4.141)

Такое же условие устойчивости, и можно полу-

чить, если вместо геометрооптических соображений использо­вать волновую оптику. Действительно, волновая оптика позво­лила нам определить размеры пятен на зеркалах, а именно по­лучить формулы (4.126). Следовательно, если условие (4.141) не выполняется, то Ш\ и ш₂ будут иметь мнимые значения, т. е. для данного резонатора невозможно получить устойчивое реше­ние в виде гауссова пучка. Таким образом, условие (4.141) од­новременно выражает как геометрооптическое условие устойчи­вости, так и условие, при котором в данном резонаторе можно наблюдать устойчивую моду ТЕМ₀₀. То, почему эти два условия совпадают, можно понять с помощью закона ABCD, описываю-

щего распространение гауссова пучка. В самом деле, пусть q$— исходный комплексный параметр пучка в плоскости £ на рис. 4.38, тогда в соответствии с (4.112) комплексный параметр q_n после п полных проходов резонатора запишется в виде

чп

_fe-

^(4.142)

где матрица с элементами А_п, В„, С_п, D_n определяется следую­щим образом:

п

_{К в}

А В\^п С D

^(4.143)