4,5, Конфокальный резонатор [8]

Теория конфокального резонатора была разработана в ска­лярном приближении Бойдом и Гордоном [9]. Чтобы изложить эту теорию, рассмотрим резонатор длиной L, причем одну зер­кальную поверхность будем описывать в системе координат (Х], у\), а другую — в системе координат (дгг, ?/.>), как показано на рис. 4.25. Ради простоты будем считать, что оба зеркала имеют в поперечном сечении квадрат со стороной 2а. В рамках скалярного приближения собственные решения даются выра­жением (4.74). В случае, когда L а, в амплитудном множи­теле можно снова положить cos 8 ^ 1 и г ж L. Для того что­бы найти соответствующее приближение для фазового множи­теля kr, мы должны вычислить сначала расстояние г между точками Р\ и Р2 как функцию координат этих двух точек, а затем полученное выражение для г разложить в степенной ряд:

_г

{\Щ(х_{х₂+у_ху^.

(4.84)

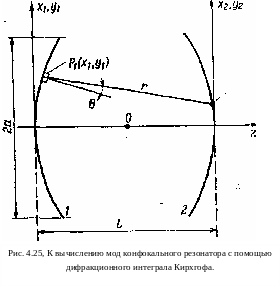
Этот ряд является достаточно хорошим приближением для k при условии, что 7V< <С L²/a², как и в случае с плоскими зеркалами. Вво­дя затем безразмерные

_{переменные | = V N(x/a)}

и ц^п^/м (у/а), вы раже -ние (4.74) " можно запи­сать в виде

o'U (|₂, _Л2) =

= -i\u(h, ri,)X

1

Xexp [-£2я(£₁|₂ + + «i dr\_u (4.85)

ГДе а*, как И Прежде, ОП­ределяется выражением

(4.79). Снова ищем ре­шение методом разделения переменных в соответствии с

В результате получаем следующие уравнения:

о-;£/₆(|₂)=ехр[-/(я/4)] j £/_e(g_I)exp(-/2ng₁|₂)rf6„ (4.86а)

(%) = ехр [— / (n/4)] j l/₄(4,)exp(-ffln_4l42)di|_r (4.866)

Физический смысл этих интегральных уравнений тот же самый, что и для плоскопараллельного резонатора. Они являются ре­шениями задачи в случае одномерных зеркал (ленточных). Уравнения (4.86) имеют конечный набор собственных решений, которые мы будем обозначать индексами m и /, т. е.

_{Um.l ft, vi) = U^m (1)£Л]' (}^T_l)'

^ат1 ^{= а}\т^а*ъг

(4.87a) (4.876)

В отличие от случая резонатора с плоскими зеркалами, послед­ние интегральные уравнения можно решить аналитически. Дей­ствительно, можно показать, что £/е_т(|) и U_nt(r\) пропорцио­нальны угловым сфероидальным функциям Фл аммера, в то

_{значения}

_и

^время

_{как соответствующие собственные}

пропорциональны радиальным сфероидальным функциям Флам-мера. Эти функции табулирован^ в работе [10]

Что касается собственных функций, то их можно найти зна­чительно более просто в случае, когда N i§> 1. При этом в урав­нениях (4.86) интегрирование можно распространить и на всю

область от -оо до +оо. В этом случае правые части уравне­ний (4.86), за исключением коэффициентов пропорциональности, представляют собой фурье-образы распределений соответственно U(h) и ^Ы-Таким образом, согласно (4.86), искомые соб­ственные функции должны быть инвариантными относительно

фурье-преобразования. Известно, что этим свойством обладает произведение гауссовой функции и полинома Эрмита, Возвра- щаясь к исходным координатам х и у, собственные функции можно записать соответственно в виде

V_xm (х) = Н_т [х (т^)"²] ехр I— (n/LX) х?], (4.88а) U_yi(у) =H_t [у(-Д^У⁷²]ехр[- {п/П)у²], (4.886)

где Н_т и Hi — полиномы Эрмита т-го и /-го порядков. Таким

образом, полная собственная функция записывается в виде

О_mix, у) =Н_тН[ ехр [- (n/LXftx² + у% (4,89)

Uxfi(x) = exp[—(л/LA,) г²].

Рассмотрим теперь несколько примеров. Если т=0, то Я₀ = 1 и из (4.88а) имеем

(4.90)

На рис. 4.26 приведены зависимости функции U от х/а для двух значений числа Френеля N. На расстоянии w_a от центра зеркала амплитуда электрического поля на нем уменьшается в

е раз относительно своего максимального значения, причем личина w$ дается выражением

w_s = (Mfn)U*. (4.91)

Если га= 1, то Яi = (8n/L%)¹ %.На рис. 4.27 приведены зави­симости нормированной величины (Jot х/а для двух значений числа Френеля. Поскольку полная модовая картина определяет­ся выражением (4.87а), мы получаем следующие моды низшего порядка:

1) Мода ТЕМоо (т = 1=0). Собственное решение записы­вается в виде Uoo(x,y) — exp 1—я(х² + у²)/Щ. Эта мода имеет гауссово распределение как в направлении *, так и в направле­нии у. В данном случае модовая картина представляет собой круглое светящееся пятно на зеркале (рис. 4.28), причем его раз­мер равен w_s. Поэтому w_s называют размером пятна на зер-

Рис. 4.26. Симметричная мода низшего порядка в конфокальном резонаторе.

кале¹*. Например, в случае % = 0,6 мкм и L = 0,5 м получаем w_s^ 0,3 мм.

2) Мода ТЕМох (т = 0, /=1). Собственное решение запи­сывается в виде Uoi(x,y)= #i(t/)exp [—п{х² + y²)/L%]\ зави­симость поля в направлении оси к такая же, как и на рис. 4.26, в то время как в направлении у амплитуда поля ведет себя так, как показано на рис. 4.27. Световое пятно, которое образуется на зеркале для этой моды, изображено на рис. 4.28.

^J> Обратим здесь внимание на возможность иной интерпретации числа Френеля. С помощью выражения (4.91) нетрудно показать, что

(а²/а>|). Отсюда мы видим, что с точностью до постоянного коэф­фициента число N равно отношению поперечного сечения зеркала (пФ для круглого зеркала) к поперечному сечению моды (nw_s на зеркале).

3) Мода ТЕМ_п (m = l=\). Собственная функция в этом случае имеет вид U_n(x, у) ~ Н_х(х) HUy) ехр \—л{х² +у²)/Щ, а соответствующая зависимость поля вдоль ос¹ей к и у приве­дена на рис. 4.27.

Аналогичным образом можно найти собственные функции и распределения мод более высокого порядка, например ТЕМ₂о и ТЕМ₃, на рис. 4.28. Следует заметить, что в общем случае ин­дексы m и / равны числу нулей поля (за исключением нулей при л-= ±оо и у = ±00) соответствен­но вдоль осей х и у.

До сих пор мы рассматривали только собственные функции урав­нений (4.86). Обращаясь теперь к собственным значениям, снова в приближении N-+oo получаем

_{°;(=exp[-/(l+m+0(«/2)],}

^(4.92)

_{Ф*т, I = ~ 0 +} ^{т + 1}_{) <}^Л_/²_{>- (4-}⁹³₎

Отсюда, используя условие находим следующее выра-

жение для резонаа^ных частот:

v

_{с [2п + (1 + m + 01}

AL

_(4.94)

Соответствующий спектр частот приведен на рис. 4.29. Следует заметить, что моды, характеризующиеся одним и тем же значе­нием суммы 2п + т + /, имеют одинаковые резонансные ча­стоты, хотя их пространственные конфигурации различны. Эти моды называются частотно-вырожденными. Заметим также, что в отличие от случая плоских волн (рис. 4.19) разность частот

_{между двумя модами (межмодовое расстояние) теперь равна}

c/AL. Однако разность частот между двумя модами с одними и теми же значениями /, m (например, ТЕМоо) и с я, различаю­щимися на единицу (разность частот между двумя соседними продольными модами), равна с/21, т. е. точно такая же, как и

_{для резонатора с плоскими зеркалами.}

Рассмотрим теперь дифракционные потери в резонаторе. Прежде всего заметим, что если воспользоваться выражением (4.92), то получим \<j*_m ,\ =1, т. е. дифракционные потери отсут­ствуют. Этот результат является следствием того, что в (4.86) мы положили N-+ оо (зеркала с очень большой апертурой).

Следовательно, чтобы рассмотрение собственных значений \а⁹_т1\ имело смысл, в уравнениях (4.86а) и (4.866) необходимо

считать величину N конечной; иными словами, необходимо рас­смотреть радиальные сфероидальные функции Фламмера. На

• • • • *

л _ ^ ■/ 7

п,0,0 _а

. . . *

п~-1 1 7

п, 0,1

_{(г 1 t~ А}

.п'*1,0,0\

C/4l

Рис. 4.29. Резонансные частоты конфокального резонатора.

рис. 4.30 показаны зависимости дифракционных потерь y<i = -1_|_а|2 от числа Френеля N, вычисленные по значениям этих функций для мод низшего порядка. Действительно, как следует из уравнений (4.86) и (4.876), а'_т , и, следовательно,

y_d должны быть функциями только параметров N,mnl. Срав­нение рис. 4.30 и 4.24 показывает, что для данного числа

1

Френеля дифракционные потери в конфокальном резонаторе зна­чительно меньше, чем в резонаторе с плоскими зеркалами. Это нетрудно понять, если заметить, что благодаря фокусирующему действию сферических зеркал поле в конфокальном резонаторе сосредоточивается главным образом вдоль оси резонатора (ср., например, кривые на рис. 4.26 и 4.21 или на рис. 4.27 и 4.23 при одних и тех же значениях числа Френеля).

Рис. 4.30. Дифракционные потери в конфокальном резонаторе за один про- I ход Yd в зависимости от числа Френеля. (Согласно Бойду и Гордону Щ)

i

Если известно распределение поля на зеркалах, то поле в \

любой точке внутри резонатора можно получить, используя \

опять интеграл Френеля — Кирхгофа. В предельном случае 'I

можно показать, что если направить ось z вдоль оси 1 резонатора и расположить начало координат в центре резона- тора, то распределение поля запишется в виде

X exp {-/[*z - (1 + m + 0*(z)]} X

X exp { - [ik (x* + y*)l2R (z)}}, (4.95)

где w (r) = w₀ [ 1 + (2z/L)²]^l/2, (4.96)

w₀ = (и/гя)"², (4.97)

R(z)^z[l + (L/2z)²], (4.98)

<f> (z) = arctg (2z/L). (4.99)

На первый взгляд выражение (4.95) кажется очень сложным, , однако ниже мы покажем, что отдельные части этого выраже- ; ния имеют простой смысл. Прежде всего заметим, что первая j

i i

строчка (4.95) представляет собой амплитуду поля Ulx, y_f z), и мы будем называть ее амплитудным множителем. Вторая строч­ка в (4.95) дает изменение фазы вдоль оси резонатора и может быть названа продольным фазовым множителем. Третья строчка выражает изменения фазы в плоскости, перпендикулярной оси резонатора, и может быть названа поперечным фазовым мно­жителем.

Чтобы изучить амплитудный множитель, рассмотрим сна­чала моду ТЕМоо. В этом случае Н_т = Я/ = const и амплитуд -

ный множитель принимает вид

(4.100)

Зерпало

_О

Выражение (4.100) показывает» что, если не учитывать множи­тель Wo/w (z), значение которого мы обсудим позже, то \U\ снова описывается гауссовой функцией, ширина w(z) которой

^{Зеркало}

Рис. 4.31. Размер пятна и поверхности равной фазы для моды ТЕМоо в кои-

фокальном резонаторе.

на уровне 1/е от максимального значения в соответствии с (4.96) является функцией продольной координаты z. Следова­тельно, в произвольной точке внутри резонатора пучок сохра­няет гауссов профиль, но размер пятна изменяется в продоль­ном направлении. На рис. 4.31 сплошными линиями показано изменение размера пятна, построенное в соответствии с выраже­нием (4.96). Заметим, что минимальный размер пятна ш = ш₀ соответствует точке 2 = 0. Поэтому величину шо, определяемую из выражения (4,97), обычно называют размером пятна в перетяжке пучка. Заметим, что при z = ±L/2 (т. е. на зеркалах) из выра­жения (4.96) имеем w = (LX/nf^/2_t что согласуется с (4.91).Таким

образом, размер пятна на зеркалах в <\J2 раз больше, чем в цен­тре резонатора. Это согласуется с тем фактом, что зеркала стре­мятся сфокусировать пучок в центре резонатора. Следует также заметить, что в гауссовом пучке расстояние между двумя точ­ками на оси пучка, в которых размер пятна в V раз больше, чем размер пятна в перетяжке пучка, называется конфокаль­ным параметром г_е. Таким образом, в рассматриваемом случае ¹ г_с равно L, т. е. в соответствии с (4.97)

г, = 2щ^/Л. (4.101) \

Рассмотрим теперь моды более высокого порядка, т, е. в ам- j плитудном множителе выражения (4.95) тфО и 1Ф0. При j этом мы видим, что распределение поля в произвольной точке ] внутри резонатора дается снова произведением гауссовой функ- \ ции на полиномы Эрмита. Поэтому распределение интенсивно- сти моды, скажем ТЕМю, сохраняется (см. рис. 4.28) в любой | точке внутри резонатора. Следует заметить, что переменные х и 1 у, входящие в выражении (4.95) в полиномы Эрмита, нормиро- I ваны на ш(г), т. е. на размер пятна. Это означает, что с измене- 1 нием w (г) размеры мод высшего порядка в радиальном напра- | влении меняются таким же образом, как и у моды ТЕМоо- По- | этому относительные размеры различных распределений попе- i речных мод сохраняются неизменными во всех точках вдоль ] пучка. i

Обратимся теперь к продольному фазовому множителю в вы- , ражении (4.95). Вначале сделаем замечание относительно того, i что, как и в интеграл Френеля — Кирхгофа (4.73), в выражение '.] (4.95) не входит временная зависимость электромагнитного поля. Интеграл Френеля — Кирхгофа можно рассматривать как | интегральное представление дифференциального уравнения 1 Гельмгольца [см. (2.5а)]. Следовательно, как и в последнем 1 случае, зависящая от времени и пространственных координат | напряженность поля получается простым умножением части * выражения (4.95), которая зависит от пространственных коор- * динат, на зависящий от времени множитель exp [± (i2rcv/)], в I котором величина v дается выражением (4.94). Выбор знака + 1 или — в экспоненте отвечает, как это следует из (4.95), волне, | распространяющейся соответственно в положительном или отри- цательном направлении оси 2. Поэтому стоячую волну внутри & резонатора можно рассматривать как суперпозицию двух этих волн. Таким образом очевидно, что входящая в (4.95) функция tj?(z) = kz — (1 + т + 1)ф (2) = kz — (1 + т + /)arctg(2z/L) описывает изменение фазы волнового фронта в зависимости от I координаты 2. Следовательно, с помощью этой величины можно найти, например, набег фазы, который приобретает волна при ее распространении в положительном направлении оси z от ле- вого до правого зеркала на рис. 4.31. Заметим, что этот набег _{

фазы не равен точно набегу фазы плоской волны, который ра­вен kz. Данное обстоятельство приводит к двум взаимосвязан- \

ным следствиям: 1) фазовая скорость гауссова пучка v = = coz/t|) (z) = Со/л [ 1 - (ty2nzarctg (2z/L) ] близка к скорости света плоской волны, хотя слегка превышает ее; 2) резонанс­ные частоты конфокального резонатора [см. (4.94) 1 отличаются от тех, которые получаются для случая плоской волны [см. (4.3)]. Действительно, из выражения (4.95) находим, что набег фазы за один проход равен [k{LJ2)-(\+т + + /)arctg(l)] - [—k(L/2)— (1 +т + /)arctg(— 1)1, что соот­ветствует соотношению (4.93), если к ft , добавить набег фазы

плоской волны kL.

Рассматривая, как и выше, две распространяющиеся на­встречу дрУг другу волны, нетрудно понять физический смысл того, почему в амплитудный множитель выражения (4.95) вхо­дит величина «>о/о»(г).Если из двух распространяющихся на­встречу волн выбрать любую из ниХ, то, поскольку мы предпо­ложили, что среда, в которой распространяются волны, не имеет потерь, полная мощность, переносимая этой волной, должна быть одной и той же в любой плоскости _Z. Отсюда следует, что

интеграл \ \ U f dx dy не должен зависеть от z. Это условие вы­полняется именно благодаря наличию величины Доо/ш (г) • Дей­ствительно, можно написать следующее выражение:

4-оо +оо

^{$$|£/|2dx<fy = (o>2/2) J #}_m^{(j) eyp(-t?)d$ J #}₂^{(Tj)exp(-r)2)dti,}

—oo — oo

где £ =^2x/ши ц = ^2y(w. Внимательно изучая это выра­жение, можно убедиться в том, что \ \ | Uf dx dy не зависит от z.

Наконец, рассмотрим в выражении (4.95) множитель, опи­сывающий изменение фазы в поперечном к оси резонатора на­правлении. Наличие этого множителя указывает на то, что пло­скости г = const не являются поверхностями постоянной фазы, т. е. волновые фронты не являются плоскими. Поэтому необхо­димо определить форму эквифазных поверхностей. В соответ­ствии с выражениями для поперечного и продольного фазовых множителей в (4.95) уравнение эквифазной поверхности, кото­рая пересекает ось z в некоторой данной точке го, запишется в виде

[ 2Д ] + ^kz~ ^kzQ> (4.102)

где мы пренебрегли очень небольшим изменением фазы (1 + + т + 0arctg(2z/L) в продольном направлении. Уравнение (4.102) показывает, что эквифазная поверхность представляет собой параболоид вращения относительно оси г. Покажем те­перь, что радиус кривизны этого параболоида в точке z = Zo в точности равен R. Для этого рассмотрим сферическую поверх­ность радиусом R, пересекающую ось z под прямым углом в точке г = Zo (рис. 4.32). Нетрудно показать, что уравнение та­кой сферической поверхности имеет вид [ (К - го + г)² + х^г + + y²]=R². При (г— z₀) «С Я это уравнение сводится к (4.102). Поэтому можно заключить, что эквифазные поверхности в хоро­шем приближении описываются сферами с радиусом кривизны

L_(x . R. Однако следует заметить,

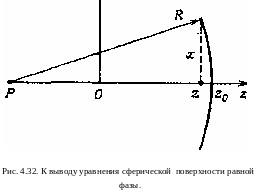^ что, согласно выражению

(4.98), этот радиус кривиз­ны зависит от координаты z Наглядные примеры эк-вифазных поверхностей по­казаны на рис. 4.31 штрихо­выми линиями для несколь­ких точек вдоль оси резо­натора. Заметим, что при 2 — 0 (центр резонатора) R = оо и волновой фронт является плоским, как и сле­довало ожидать из сообра­жений симметрии. Заметим также, что при z = ±L/2 (т. е. на зеркалах) R = ±L. Отсюда следует, что вблизи зеркал экви­фазные поверхности совпадают с поверхностью зеркал. Это можно объяснить исходя из следующих двух соображений; 1) если рассматривать поле в виде распределения стоячих волн и считать, что оба зеркала металлические, то на поверхности обоих зеркал напряженность поля должна обращаться в нуль, а отсюда следует, что на этих поверхностях поле должно иметь одну и ту же фазу; 2) если поле представить в виде суперпози­ции бегущих волн, то волна, распространяющаяся, скажем,

вправо на рис. 4.31, после отражения на зеркале 2 должна пре­образоваться в волну, бегущую влево. С точки зрения геометри­ческой оптики лучи вблизи зеркала 2 должны быть перпендику­лярны поверхности зеркала. Отсюда следует, что перпендику­лярная этим лучам эквифазная поверхность должна совпадать

^{с поверхностью зеркала.}

До сих пор мы рассматривали распределение поля только внутри резонатора. Впрочем, вычисление поля вне резонатора

⁴⁾ В выражении (4.95) радиус К считается положительным, когда цен кривизны располагается слева от волнового фронта.

не вызывает теперь затруднений. Действительно, мы видели, что

4.6. Распространение гауссова пучка и закон ABCD 207

распределение поля внутри резонатора можно рассматривать как результат суперпозиции волн, одна из которых распростра­няется на рис. 4.31 вправо, а другая - влево. Если оба зеркала частично прозрачны, то зеркало 2 будет пропускать лишь волну, распространяющуюся вправо, а зеркало 1 - волну, распростра­няющуюся влево (см. рис. 4.31). Это означает, что как выраже­ние (4.95), так и (4.96) — (4.99) справедливы в любой точке вне резонатора. Например/электромагнитное поле, выходящее, ска­жем, из зеркала 2, получается умножением U(x,y, _z) в (4.95)

на ехр/7 (2jwf)] •