4.2.2. Интерферометр Фабри—Перо [2]

Следующий предмет традиционной оптики, который мы рас­смотрим, представляет собой многократная интерференция. Это явление имеет место в интерферометре Фабри — Перо, который является обычным спектроскопическим прибором и со времени его изобретения в 1899 г. играет очень важную роль в лазерной физике. Большая его популярность объясняется по крайней мере тремя различными причинами; 1) физические процессы,

EfEotjizexpW)

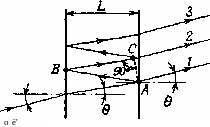
^{Рис, 4.12. Многолучевая интерференция в интерферометре Фабри — Перо.}

происходящие в нем, на фундаментальном уровне аналогичны тем, что имеют место в оптических резонаторах; 2) во многих случаях его применяют для селекции частот внутри лазерного резонатора; 3) его нередко используют для анализа спектра ла­зерного излучения. Поэтому в настоящем разделе мы рассмот­рим свойства этого интерферометра, хотя и не очень подробно.

Интерферометр Фабри — Перо состоит из двух плоских и параллельных друг другу зеркал с коэффициентами отражения по мощности Rx и R₂ ^п, разделенных промежутком длиной L, заполненным средой с показателем преломления п_г. Рассмот­рим плоскую волну с частотой v, падающую на интерферометр в направлении, составляющем угол 6' с нормалью к обоим зеркалам (рис. 4.12). Эта волна схематически изображена на рис. 4.12 лучом О. Выходной пучок, покидающий интерферо­метр, представляет собой суперпозицию пучка, прошедшего через оба зеркала (луч 1 на рис 4.12), с пучками, возникаю­щими благодаря многократным отражениям,—два из этих пуч­ков указаны лучами 2 и3 на рис.4.12. Таким образом, ампли­туда электрического поля выходного пучка Et получается суммированием амплитуд £, всех этих пучков с учетом соответ­ствующих фазовых сдвигов. Для иллюстрации данного рассмот­рения на рис. 4.12 приведены также выражения для электриче­ского поля первых трех пучков. Если учесть все многократные

отражения, то мы получим

оо оо

_{Et = Е Ег = [Е№&*+'\ Z (г!Г2)}^ш_{ехр (2mif). (4.21)}

1=1 m-0

В этом выражении, как и на рие. 4.12, £о — амплитуда пучка, падающего на интерферометр; /, и fe - коэффициенты пропу- скания для электрического поля обоих зеркал, соот- ветствующие коэффициенты отражения для электрического поля; ф'— фазовый набег при однократном прохождении, вклю- чающий в себя также и набеги фазы при прохождении обоих зеркал; 2ф— сдвиг фазы между последовательными отраже- ниями, равный

2ф = kL_s = 2kL cos 0 = " L cos 8 ; (4.22)

здесь L_s — сумма длин двух отрезков АВ и ВС на рис. 4.12, а угол 0 связан с углом 6' законом Снеллиуса (n_rsin9 = sin 8'). "Заметим, что (4.22) можно переписать в более простом виде:

ф = 2nL'vJc₀, (4.23)

где

I' = rt_rLcosB. (4.24)

Сумму геометрической последовательности, входящую в выра­жение (4.21); нетрудно вычислить, и мы имеем

^{В, - Б** - _ . ,(4.25)}

Коэффициент пропускания Т интерферометра по мощности равен просто | E_t f/\ E_Q j², и из (4.25) находим

_{Т = Li _. (4.26)}

1 — 2г,г₂ cos +

₁

_i

₁

^{1 — R}_{ ^{и /|}

^{Поскольку Я, — г\, Я}₂ ^{= т\, а для зеркала без потерь i\ =}

.2

—

2

^R₉^{, выражение (4.26) пре-}

I

^{; »}

I

образуется к виду

_{Т =}

_{(1 — Я|)}

(4.27)

Это выражение и есть окончательный результат наших вычис­лений.

Для иллюстрации свойств интерферометра Фабри — Перо на рис. 4.13 построена зависимость п^оПускания Т интерферометра

AVfisr

№4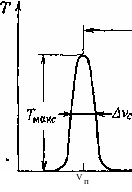

V

Рис. 4,13. Пропускание интерферометра Фафи —Перо в зависимости от час-

_{Ф =пя;}

от частоты v падающей волны, причем пропускание Т⁷ вычисле­но по формуле (4,27), в которой ф определяется выражением (4.23). Заметим, что кривая состоит из последовательности рав-нестоящих максимумов. Эти максимумы наблюдаются, когда в (4.27) sin² ф = О, т. е. когда

(4.28)

здесь п жением равны

/

- положительное целое число. В соответствии с выра-(4.23) частоты v,„ соответствующие этим максимумам,

_(4.29)

Последнее явно напоминает условие (4.3). Физиче-

ский смысл этого можно понять, если заметить, что в максиму­ме пропускания, т. е. когда ф=пл, все волны, образующиеся вследствие многократных отражений, находятся в фазе. По при­чинам, которые станут ясными в конце этого раздела, разность

частот между двумя соседними максимумами Avf_Sr называется свободной спектральной зоной ^!> интерферометра. Из формулы (4.29) нетрудно получить

^Av_fsr ⁼ _C^{J2L'. (4.30)}

Максимальное пропускание находим из выражения (4.27):

[1 _ (_Л|/?2)1/2]2 • V'*¹'

Заметим, что, если Ri= R₂ = Д, то /макс — 1 независимо от ве­личины коэффициента отражения зеркала JR. Этот результат справедлив лишь в тех случаях, когда, как в нашем рассмотре­нии, можно пренебречь поглощением излучения в зеркалах (см. задачу 4.3). Минимумы пропускания достигаются при sin²^ = 1, т. е. они располагаются посередине между соседними максимумами. Пропускание в точке минимума находим из вы­ражения (4.27):

^м"^й [1 + (Я,*,)"²]² " ^{{ }}

Следует отметить, что при обычных условиях величина Г_Ш1н очень мала. Если, например, выбрать R\— R₂ = 0,98, то Т_тт »

Чтобы вычислить ширину пика пропускания Av*_f заметим, что в соответствии с формулой (4.27) пропускание упадет до половины своего максимального значения при смещении Аф от угла ф = пк, которое определяется выражением

4(/?₁/?₂)^l'²sin²A^ - [1 - (i?,i?₂)^l/2]². (4.33)

Полагая Аф < я/2, можно считать, что sinA^ « Аф. Тогда из выражения (4,33) получаем

Аф^ ± [1 - (R_XR^%R_XR^\ (4.34)

откуда следует, что две точки на половине интенсивности мак­симума, соответствующие Аф+ и расположены симметрично по обеим сторонам максимума. Если положить Аф_€ = Аф+— — Аф-, то из последнего выражения имеем

^^=±1Ш^ ⁽⁴-³⁵⁾

*> Вместо термина «свободная спектральная зона» (буквальный перевод англ. слов free spectral range, сокращенно fsr) в советской литературе чаще употребляется термин «область дисперсии». Последний мы и будем исполь­зовать в дальнейшем. — Прим. ред.

1/2

и с учетом (4.23)

Av,

_{со 1 - {RiRi)}

2L' n{R_xR₂)^[fA

(4,36)

Определим теперь резкость F интерферометра как

F = Avfsr/Av*.

Из выражений (4.30) и (4.36) получаем

я<№)^1/4

1 - <*!*»)

(4.37)

(4.38)

Резкость— это число, обычно много большее единицы, указы­вающее, насколько узка линия пропускания по сравнению с

областью дисперсии. Рассмотрев снова случай i?j = R₂ = 0,98, по­лучаем F tt 150.

После этого общего описания свойств интерферометра Фабри— Перо рассмотрим теперь его при­менение для анализа спектра. Изучим простейший случай, ког­да интерферометр заполнен воз­духом (п_г « 1) и падающий свет направлен перпендикулярно зер­калам интерферометра (т. е. cos 9 = 1). Предположим, что длину L можно менять в лак нескольких длин волн, при-Рис. 4.14. Пропускание по интен- крепив, например, одну из двух

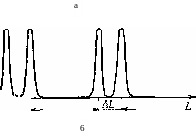
снвности сканирующего интерфе- пластин интерферометра к пьезо-когдТпадающаГвмна мош™' электрическому преобразователю

матическая (а) и когда она Со- ^{(сканирующий интерферометр}

_{стоит из двух воли с близкими Фабри-Перо). Чтобы понять,}

частотами (б). что происходит в этом случае,

рассмотрим вначале монохрома­тическую волну с частотой v и длиной волны Я. Из предыду­щих рассуждений следует, что прошедший свет будет иметь максимумы при ф = /т, т. е. когда длина интерферометра равна (см. рис. 4.14, а)

L = nl/2)

_(4.39)

здесь п — положительное целое число. Изменение длины L, не­обходимое для перехода с одного пика пропускания на сосед­ний, равно

Миг = Я/2. (4.40)

1

"I

i * - — - — —

Ширина каждого пика пропускания AL_C должна удовлетворять условию

(2яч/с₀)№_е = Аф_е, (4.41)

где Афс дается выражением (4.35). Следовательно, по аналогии с (4.37) можно написать

AL_C = ALtsr/F. (4.42)

Рассмотрим теперь случай, когда на интерферометр падают две волны с частотами v и v + Av. Волна с частотой v + Av приве­дет к образованию максимумов пропускания, смещенных на расстояние AL от всех тех, которые образуются волной с часто­той v (рис. 4.14,6"). В соответствии с условием (4.28) смещение AL должно удовлетворять соотношению

(2/с₀) (L + AL) (v + Av) = пп. (4.43)

Поскольку 2nLv/c₀ = пп,

AL = - (Av/v) L. (4.44)

Две частоты v и v + Av будут разрешены спектрометром, если

AL > AL_e. (4.45)

_{Минимальный частотный интервал Avm, который еще может}

быть разрешен, получается, когда в (4.45) имеет место равен­ство. Из выражений (4.42), (4.44) и (4,45) при этом получаем

Av_m = Avf_sr/F. (4.46)

Таким образом, резкость интерферометра определяет его разре­шающую способность через область дисперсии.

Следует заметить, что когда IALI = AZ,t_sr, т. е. когда Av = = Av_fSr=c₀/2L, максимумы пропускания на частотах v + Av и v совпадают, хотя они и сдвигаются на один порядок по отно­шению друг к Другу. Поэтому, когда > Avfsr, в измерении Av появляется неоднозначность в размере целого числа областей дисперсии Avfsr. Таким образом, в случае когда интерферометр используется для измерений разности частот, мы получаем про­стой и однозначный результат лишь при Av < Av_fsr, откуда и следует название Avfsr как области дисперсии (свободной спект­ральной зоны) интерферометра. Представленный выше резуль­тат нетрудно обобщить следующим образом: если Д\>ен — спек­тральная ширина линии падающего света, то, чтобы избежать неоднозначности в определении частоты, необходимо, чтобы AweH ^ Avfsr. Если в этом соотношении выполняется равенство, то из (4.46) получаем

Av_m = Av_reH/F. (4.47)

Таким образом, резкость также служит показателем того, на­сколько резко мы можем разделять частоты в пределах полной спектральной ширины Av_reH. Например, если выбрать Av_reH = = 1,5 ГГц и F=150, то Av«= 10 МГц. Если длина электро­магнитной волны равна % = 0,5 мкм (зеленый свет), то Av«/ /v« 1J-Ю-⁸. Это очень высокая разрешающая способность по

в

Рис. 4.15. Кольца Фабри — Перо, образующиеся в фокальной плоскости лин­зы при падении на интерферометр Фабри — Перо рассеянного пучка, а — схема эксперимента; б — наблюдаемый кольцевой рисунок в фокальной пло­скости (рис. а) в случае, когда падающая волна является монохроматиче­ской; в — кольцевая картина в случае, когда падающий пучок состоит из

двух монохроматических волн.

сравнению, например, с тем наилучшим разрешением, которое может быть достигнуто в спектрометре с дифракционными ре­шетками (Av/v = 10~⁵—10~⁶).

Другой известный способ применения интерферометра Фаб­ри—Перо показан на рис. 4.15. Рассеиватель, такой, как пла­стинка матового стекла или даже простая линза, помещается на пути падающего пучка, чтобы обеспечить широкий набор углов падения для света, попадающего в интерферометр Фаб­ри—Перо. Таким образом, волну, падающую на вход интерфе­рометра, можно рассматривать как суперпозицию плоских волн, распространяющихся в различных направлениях. Свет, прошед­ший через интерферометр с определенной длиной, собирается при этом линзой в ее фокальной плоскости. Рассмотрим снача­ла пучок монохроматического света с частотой v и предполо­жим, что промежуток между двумя зеркалами интерферометра

заполнен воздухом (n_r = 1). Тогда в соответствии с условиями (4.28) и (4,22) максимумы пропускания будут наблюдаться при тех углах 0_Л, которые удовлетворяют соотношению

cosQ_n = n%/2L. (4.48)

Если рассматривать только те пучки, направления распростра­нения которых лежат в плоскости рис. 4.15, а, то для каждого угла 9л в фокальной плоскости будут наблюдаться две яркие точки Р и Р'. Рассмотрим теперь весь набор падающих лучей, а не только те, что в плоскости рисунка. Мы видим, что про­шедший свет, соответствующий углу 6„, образует в фокальной плоскости яркую окружность радиусом

г = OP = fig Q_n, (4.49)

где / — фокусное расстояние линзы. Если учесть все возможные углы е„, то пропущенный свет образует в фокальной плоскости набор концентрических колец, радиусы которых нетрудно най­ти из выражений (4.48) и (4.49) (рис. 4.15,6). Если теперь рассмотреть второй пучок при частоте v + Av, то в фокальной

^{плоскости образуется второй набор концентрических колец,}

слегка смещенных по радиусу относительно колец первого на­бора (рис. 4.15, в). Как и для сканирующего интерферометра Фабри-Перо, в данном случае нетрудно показать, что 1) для устранения неоднозначности в определении частоты необходимо иметь Av < Avfsr; 2) если Av < Av_fsr, то два набора колец бу­дут разрешены в том случае, когда Av > Avtsr//⁷, где F— рез­кость интерферометра.