4.2. Некоторые разделы геометрической и волновой оптики

Прежде чем приступить к подробному обсуждению оптиче­ских резонаторов, уместно рассмотреть в этом разделе некото­рые вопросы геометрической и волновой оптики, которые обыч­но не входят в элементарные учебники по оптике, но которые составили бы весьма полезный фундамент для данной главы. Таким образом, в разд. 4.2.1 мы дадим введение в матричную формулировку геометрической оптики в рамках приближения параксиальных лучей. В разд. 4.2.2 и 4.2.3 рассмотрим много­численные интерференционные явления, которые имеют место соответственно в интерферометре Фабри - Перо и многослой­ном диэлектрическом покрытии.

4.2.1. Матричная формулировка геометрической оптики [1]

Рассмотрим луч света, который либо проходит через обра­тимый и поляризационно-независимый оптический элемент (на­пример, линзу или зеркало), либо отражается от него. Если луч распространяется приблизительно вдоль оси z, то лучевой вектор г, на данной входной плоскости z = г_х оптического эле­мента (рис, 4.7) можно описать двумя параметрами:

	У	г
	t - ' Оптический.		г- z
	элемент

2_Г z_g

Рис. 4.7, К матричному представлению распространения луча через пронз-

' вольный оптический элемент.

его радиальным смещением r\(z\) от оси г и угловым смещением 6_Ь Аналогичным образом лучевой вектор г₂ на выходной плоско­сти 1 = 2.2 можно определить его радиальным г₂ (г₂) и угловым 62 смещениями. В приближении параксиальных лучей угловые смещения 9 предполагаются достаточно малыми, ' так что мы можем записать sin 9 ~ tg 9 ж 9. В этом случае выходные (гг, 92) и входные (ги 60 переменные связаны друг с другом линейным преобразованием» Таким образом, если положить 8j (drJdz) — г[ и 9₂ ft* (dr₂jdz) — r'_2> то мы имеем следую­щие соотношения:

r₂ = Л^ + Вг^, (4.4а)

r'₂ = Cr_l + Dr'_l, (4.46)

где Л, В, С и D — постоянные, характеризующие данный оптический элемент. Поэтому естественно записать (4.4)

^{в матричном виде:}

		А	В
Г2		С	D		г' 1

(4.5)

где матрица A BCD полностью характеризует данный оптиче­ский элемент в приближении параксиальных лучей.

_а

	1	1 Д }
\ Г J		t 1	1	i 4 1

^{в \R}

Рис. 4.8, К вычислению ЛЯСД-матрицы для случаев свободного распростра­нения луча (й), распространения через линзу (б) и отражения от сфериче­ского зеркала (в).

В качестве первого и простейшего примера рассмотрим сво­бодное распространение луча на расстояние Az = L в данной среде с показателем преломления п (рис. 4.8, а). Если входная и выходная плоскости расположены в непосредственной бли­зости от данной среды, но в среде с показателем преломления, равным единице, то

_{г'— г'}

(4.6а) (4.66)

и соответствующая Л BCD-матрица запишется в виде

1 Цп О 1

(4.7)

В качестве следующего примера рассмотрим распространение луча через линзу с фокусным расстоянием f (будем считать f положительным для собирающей линзы). Для тонкой линзы, очевидно, имеем (рис. 4.8, б)

г₂ = г_{. (4.8а)

Второе соотношение получается из хорошо известного закона геометрической оптики, а именно l/q = l/f, с учетом того,

что р = ^r{j^r\ и Ц = —^r₂/^rr Используя соотношение (4.8а), находим

г£ = — (l/f) r_t ч- г\. (4.86)

В соответствии с (4.8а) и (4.86) Л BCD-матрица в этом случае запишется в виде

1 01

-l/f 1 ' *⁴*⁹'

Третий пример представляет собой отражение луча сфериче­ским зеркалом с радиусом кривизны R (будем считать R по­ложительным для вогнутого зеркала). В этом случае плоскости z\ и 2₂ выбирают таким образом, что они совпадают одна с дру­гой и располагаются непосредственно перед зеркалом. За по­ложительное направление оси г берется направление слева направо для падающего вектора и справа налево для отражен­ного. С учетом этих соглашений лучевая матрица вогнутого зер­кала с радиусом кривизны R и, следовательно, фокусным рас­стоянием f = R/2 совпадает с матрицей для положительной линзы с фокусным расстоянием f. Таким образом, лучевая мат­рица запишется в виде

_{1 О}

_{2//? 1}

(4Л0)

В качестве общего замечания, которое справедливо во всех трех рассмотренных случаях, укажем на то, что определитель Л BCD-матрицы всегда равен единице, т. е.

AD — BC=l. (4.11)

В табл. 4.1 мы привели лучевые матрицы для рассмотренных выше оптических элементов, а также для сферической границы раздела двух диэлектриков (задача 4.1). Заметим, что опреде-

литель Л BCD-матрицы равен единице только тогда, когда пока­затели преломления на входной и выходной плоскостях одина­ковы.

Таблица 4.1. Лучевые матрицы для некоторых широко распространенных случаев

_IS

Распространение в свободном

пространстве

_{.0 1 J}

Тонкая линза

1 О

Сферическое зеркало

О

Сферическая граница раздела диэлектриков

^{/ о'}

п₂ R п_г

Если известны матрицы элементарных оптических компо­нентов» то полную матрицу сложной оптической системы не­трудно получить путем разбиения ее на эти элементарные ком­поненты. Действительно, предположим, что внутри данного оптического элемента можно рассмотреть промежуточную плоскость с координатой г/ (рис. 4.9) таким образом, что две А5С£)-матрицы между плоскостями z ⁼ г\ и г = Zi_% а также между плоскостями г = г/ и z - 22 известны. Если координаты лучевого вектора на плоскости z ⁼ z/ обозначать через ri и г\_у

то, очевидно, можно написать

		Л,			>1
Л		с,			г'
Г 2		А 9	Во		г,
г' '2		с2	®2

^(4.12а)

(4.126)

(4.13)

выражение (4.12а) для вектора r_if

Если в (4.126) подставить то получим

		А,	В2		Ai	Я,
		с2			с,			А

Таким образом, полную Л BCD-матрицу можно получить пере­множением ЛВС2)-матриц элементарных оптических компонен­тов. Заметим, что порядок, в котором матрицы располагаются

_{z — 2 ■}

Z

Z

Рис. 4.9. Распространение луча через три различные плоскости в случае, когда две матриць: между плоскостями г, L г₂ и г = г_и а также плоско­стями г = Я и z - Z2 известны. '

в произведении, является обратным по отношению к порядку, в котором световой луч проходит соответствующие оптические элементы. В качестве первого и, возможно, тривиального при­мера рассмотрим в среде с показателем преломления п сво­бодное распространение на расстояние L_u за которым следует опять свободное распространение на расстояние L₂. В соответ­ствии с (4.7) общее матричное уравнение можно записать в виде

_{0 1}

_{0 1}

(4.14)

Применяя хорошо известные правила перемножения матриц, нетрудно показать, что произведение двух квадратных матриц

дает результирующую матрицу:

^{1 (b + Ljfn}

_{0 1}

(4.15)

Это вычисление подтверждает тот очевидный вывод, что ре­зультирующее распространение эквивалентно свободному рас­пространению на расстояние L — L\ + L2. В качестве менее тривиального и более полезного примера рассмотрим свобод­ное распространение на расстояние L (в среде с показателем преломления п= 1) с последующим отражением от зеркала с радиусом кривизны R. В соответствии с (4.7), (4.10) и (4.13) результирующая Л BCD-матрица запишется в виде

Л В		1 0		1 L
С D		-щ 1		0 1

1

-2/R I

L

(2Щ)

(4.16)

Заметим, что определители обеих матриц (4.15) и (4.16) снова равны единице, причем это выполняется для произвольной по­следовательности оптических элементов, так как определитель произведения матриц равен произведению определителей.

Представленная выше матричная формулировка может быть весьма полезной для описания оптического резонатора в при­ближении геометрической оптики. Этот подход мы применим в разд. 4.7.3 для исследования устойчивости оптического резо­натора из двух сферических зеркал.

Матричная формулировка полезна не только для описания поведения луча, проходящего через оптическую систему, но также и для изучения распространения сферической волны. Действительно, рассмотрим сферическую волну, исходящую из точки Р_х рис. 4.10 и распространяющуюся вдоль оси г в поло­жительном направлении. После прохождения оптического эле­мента, описываемого данной Л BCD-матрицей, эта волна пре­образуется в новую сферическую волну с центром в точке Р₂. Рассмотрим два сопряженных луча п и Г2 двух сферических волн. Радиусы кривизны и R₂ сферических волн на входной z = z\ и на выходной z = z₂ плоскостях оптического элемента даются выражениями

_^2 ^{= Г}_%1^Г_'г

(4.17а) (4.176)

Заметим, что в (4.17) мы использовали соглашение» что R яв­ляется положительной величиной, если центр кривизны находит­ся слева от волнового фронта. Из выражений (4.4) и (4.17)

имеем

_{/?2 = (ЛЯ{ + B)I(CRX + D). (4.18)}

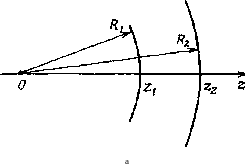
Выражение (4.18) является весьма важным результатом, поскольку оно устанавливает простое соотношение между ра­диусом кривизны R₂ выходящей волны с радиусом кривизны Ri входящей волны посред­ством элементов ABCD-mslt-рицы данного оптического элемента. В качестве пер­вого элементарного примера рассмотрим свободное рас­пространение сферической волны между точками с ко­ординатами z\ и 22 на рис* 4.11, а. С помощью выраже­ния (4.7), полагая в нем п = 1 и L = z₂ — z\ и ис­пользуя (4.18), получаем

^R₂ ^{= R}_l ^{+ (z}₂^-z_l^{), (4.19)}

что является ре-

зультатом. Теперь обратим- ся к сферической волне, про- ходящей через тонкую лин- зу (рис. 4.11,6). Из выра- j жений (4.9) и (4.18) нахо- ⁰

дим соотношение Рис. 4.П. Распространение сферической

,_{£ (А 0}пч волны в свободном пространстве (а) и \/R₂ = - l/f; (4.20) через линзу (б).

это есть не что иное, как знакомое правило геометрической оптики р^-1 + q~² = f ³.

Хотя два примера на рис, 4.11 представляют собой весьма элементарные применения выражения (4.18), полезность этого выражения можно полностью оценить, если рассмотреть про­хождение сферической волны через более сложную оптическую систему, состоящую, скажем, из последовательности линз и промежутков между ними. В этом случае радиус кривизны вы­ходящей волны опять определяется выражением (4.18), а пол­ная ABCD-uarpmia будет равна произведению элементарных матриц каждого оптического элемента. В разд. 4.5 будет пока­зано, что обобщение выражения (4.18) является очень мощным средством для описания распространения лазерного пучка.