3.3.2. Возбуждение электронным ударом

Выше мы уже упоминали о том, что электронные удары включают в себя как упругие, так и неупругие столкновения. При неупругом столкновений атом может либо возбуждаться на более высокий уровень, либо стать ионизированным.

Для простоты рассмотрим вначале ударное возбуждение коллимированным пучком моноэнергетических электронов. Если р_е — поток электронов (число электронов в единицу времени через единицу площади), то полное сечение столкновения д_е можно по аналогии с определением, которое мы

давали в случае потока фотонов [см. выражение (2.84)], а именно с помощью выражения

dF_e = -a_eN_gF_edz, (3.31)

где dF'_е — изменение потока, которое имеет место, когда пучок электронов распространяется в среде на расстояние йг. Столк­новения, которые приводят к возбуждению электронным ударом, определяют лишь некоторую часть этого полного сечения! В действительности наибольшим является сечение упругих столкновений o_et. Сечение a.i по порядку величины составляет около Ю-¹⁶ см². Если сечение электронного возбуждения ча­стицы с основного на верхний лазерный уровень обозначить че­рез 04>2, то в соответствии с выражением (3.31) скорость засе­ления верхнего состояния под действием накачки запишется

в виде

(dNJdt)^ a_e2N_gF_e= N_gN_evo_e2i (3.32)

где v — скорость электронов, а N_e — их плотность. Чтобы вы- числить скорость накалки, необходимо знать величину с_е2, ко- торая в свою очередь зависит от энергии Е налетающего элект- рона, т. е. 0,2 = о_е2 (£). Однако в газовом разряде электроны имеют некоторое распределение по энергии. В таком случае ско- рость верхнего уровня можно найти из выражения

(3.32) усреднением его по этому распределению. Таким образом, мы получаем следующее выражение;

где

{dN^jdi)_p = N_gN_e (va_e2\ (3.33)

<оа> = ^С vo (E) f(E) dE. (3.34)

В соответствии с (1.10) и (3.33) скорость накачки дается вы­ражением

W_p = N_e(va)₉ (3.35)

где <иа> вычисляется с помощью (3.34). Таким образом, для вычисления W_p необходимо знать две величины, а именно а и f, зависимость которых от энергии мы рассмотрим теперь более детально.

3.3.2.1. Сечение электронного удара [13]

рис. 3.20 качественная зависимость а от энер-

гии электронов Е для трех следующих случаев перехода; 1) оп- тически переход; 2) оптически запрещенный

п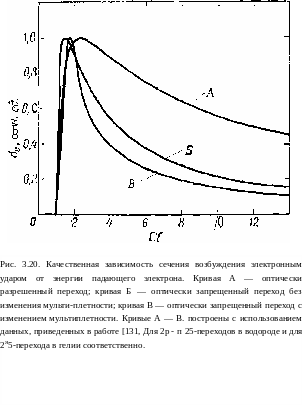 ереход без изменения мультиплетности; 3) оптически запрещен­ный переход с изменением мультиплетности. Во всех трех слу­чаях максимальное значение а нормировалось на единицу. Заметим, что в любом случае для сечения имеется четко выражен­ный порог Еиор. Как и следовало ожидать, значение £пор ока­зывается близким к энергии рассматриваемого перехода. После порога сечение резко возрастает, достигает максимального зна­чения и далее медлен­но спадает. Макси­мальное значение 0 и ширина кривой зави­сят от типа участвую­щего перехода. 1) Для оптически разрешен­ного перехода макси­мальное значение а обычно составляет 1(Н⁶ см², а ширина кривой может быть в 10 раз больше, чем пороговая энергия £_Пор (кривая А на рис. 3.20). 2) Для оптически запрещен­ных переходов без из­менения мультиплет-

ности максимальное се- чение резко падает почти на три порядка (до значения около Ю^-19 см²), а ширина кривой может быть всего в 3—4 раза боль- ше пороговой энергии (кривая Б на рис. 3.20). 3) В случае когда происходит измене- ние мультиплетности, максимальное сечение может быть боль- ше, чем для оптически запрещенного перехода, а ширина кри- вой теперь, как правило, равна или несколько меньше порого- вой энергии £_ПОр (кривая В на рис 3.20). Следует заметить, что во трех случаях ширина кривой сравнима с пороговой

энергией, т. е. с энергией перехода. Это поведение существенно отличается от того, которое мы имели для сечения поглощения фотонов. Как мы показали в разд. 2,3.3, энергетическая ширина линии в зависимости от механизма уширения может составлять 10~⁶—10~⁴ часть энергии перехода, т. е. ширина переходов, обусловленных взаимодействием с фотонами, оказывается зна-

1 *

чительно более узкой, чем при соударениях с электронами. Это объясняется тем, что возбуждение электронным ударом в прин­ципе не является резонансным явлением, т. е. любой излишек энергии уносится в виде энергии рассеянного электрона. Именно это обстоятельство является основной причиной того, что воз­буждение газообразной среды производится значительно более эффективно «полихроматическим» источником электронов (та­ким, как газовый разряд), чем полихроматическим источником света (таким, как лампа).

Чтобы иметь более глубокое представление о механизмах, участвующих в возбуждении электронным ударом, опишем квантовомеханический расчет сечения а. Для оптически разре­шенных или оптически запрещенных переходов без изменения мультиплетности наиболее простым (и во многих случаях даю­щим наибольшую точность) является расчет с использованием борновского приближения. Пучок моноэнергетических электро­нов, падающий на атом, описывается функцией плоской волны вида exp(tko-r). Здесь k_Q = 2я/Я, а X — дебройлевская длина волны электрона [Х= (12,26/V) А, где энергия электрона в электровольтах]. Между падающим электроном и электро­нами атома действует сила электростатического отталкивания. Это взаимодействие считается достаточно слабым, так что ве­роятность атома совершить переход при соударении очень мала, а возможностью сразу двух таких переходов можно пренебречь. В этом случае уравнение Шрёдингера для рассматриваемой за­дачи может быть линеаризовано. При этом в сечение перехода

будет входить множитель вида \ u*₂expli [(k₀ ^— "О * г]}^_х^К ,

где ii\ и щ — волновые функции соответственно основного и возбужденного состояний атома, a *_rt — волновой вектор рас- сеянного электрона. Если затем предположить, что длина вол- ны электрона К = 2n/ko намного превышает размеры атома, то отсюда с учетом выражения для длины волны де Бройля сле- дует, что энергия электрона Е не больше нескольких электрон- вольт. В этом случае множитель exp{/[k₀ — к,_;) «г]} в вышепри- веденном интеграле можно разложить в ряд по степеням ради- ус-вектора г, который определяет положение относительно атома. Для оптически разрешенных переходов в разложении экспоненты exp[i(k-r)] мы удерживаем лишь первый ненулевой член (т. е. /к-г, где к = к₀ — к_л), а отсюда следует, что сечение пропорционально |й|², где |р,|² определяется выражением (2.28). Мы видим, что в случае оптически разрешенного пере- хода сечение возбуждения электронным ударом о_е зависит от того же матричного элемента ||х|, который входит в выраже- ние для сечения фотона. Таким обрязом, можно

^I

ожидать, что для оптических переходов сечение

возбуждения электронным ударом будет также велико. В слу­чае оптически запрещенных переходов без изменения мульти­плетности (AS = 0; например, переход l¹S->-2^IS в атоме Не; см. рис. 6.5) борцовское выражение для сечения дает ненулевое значение следующего по порядку члена в разложении ехр [i (к -г)]. Это означает, что о* теперь пропорционально вели-

_чине

е \ и*₂х²и_л йх

2

а не, как в предыдущем случае, величине

е \ u\xu_xdx , которая теперь равна нулю, поскольку и_г и и%

имеют одну и ту же четность. Следует заметить, что выражение для а, полученное для данного случая, полностью отличается от соответствующего выражения, справедливого в случае взаи­модействия с фотоном, т. е. магнитодипольного взаимодействия. Поэтому не удивительно, что \ рассматриваемом случае отно­шение максимальных сечений (Тзапрещ/^разреш составляет около в то время как то же отношение для поглощения фотона имеет величину порядка 10~⁵, что было установлено выше [см. выражение (2.45)]. Отсюда можно сделать вывод, что возбуж­дение оптических переходов электронным ударом осуществля­ется относительно легко по сравнению с «фотонным ударом», и это имеет весьма важные последствия для большинства газовых лазеров, поскольку накачка в них часто осуществляется через

оптически запрещенные переходы.

В случае перехода с изменением мультиплетности (напри- мер, YS^S в Не; см. рис. 6.5) борновское приближение дает нулевое Течение в любом порядке разложения экспоненты ехр [/(k-r)]. Действительно, в таком переходе происходит изме- *

нение спина, в то время как в рамках борцовского приближения i

_{падающий электрон через электростатическое взаимодействие с}

ним может оказывать влияние лишь на орбитальное движение

атома, а не на его спин Ч Теория для этого случая разработана 1

Вигнером, а ее исходным постулатом служит тот факт, что при ,<|

столкновении должна сохраняться сумма полного спина атома

и спина падающего электрона, но не обязательно спина непос- *

редственно атома. Следовательно, переходы могут осуществ- '

ляться за счет столкновения с обменом электронами, когда на­летающий электрон замещает электрон атома, участвующего в переходе, и этот электрон в свою очередь вылетает из атома (однако в процессе столкновения оба электрона квантовомеха-ни чески неразличимы). Для сохранения полного спина спин на-

" Отсюда следует, что спин-орбитальное взаимодействие пренебрежимо мало» а это справедливо для легких атомов (например, для Не, Ne) и не­верно для тяжелых атомов типа Hg.

летающего электрона должен быть противоположен спину вы­летающего электрона. Из нашего краткого обсуждения этого случая можно заключить, что рассмотренный здесь обменный механизм должен иметь более резонансный характер по срав­нению с механизмом, полученным в борновском приближении. Действительно, большая вероятность первого обмена будет лишь в том случае, когда энергия налетающего электрона близка к энергии перехода. Теперь становится ясным, почему ширина резонансной кривой на рис. 3.20 (кривая В) является наименьшей из трех представленных на этом рисунке. Однако при резонансе величина о_е должна иметь большое значение. По­этому не удивительно, что максимальное сечение может быть даже больше, чем в случае оптически разрешенных переходов без изменения спина.