3.2.1. Кпд накачки

Определим КПД накачки ть непрерывного лазера как отно­шение минимальной мощности накачки Р_п, необходимой для создания определенной скорости накачки, к электрической мощ­ности накачки Р, фактически подведенной к лампе. Заметим, что в соответствии с выражением (1.10) минимальная мощность

накачки может быть записана в виде P_m = (dN2/dt)_pVhvp= — W_pNgVhv_p,me V— объем активной среды, v_p — разность ча­стот между основным и верхним лазерным уровнями. Действи-

тсльно, как мы покажем более подробно в разд. 3.2.3, распреде­ление скорости накачки но активному стержню во многих слу­чаях является неоднородным. Поэтому более правильно опреде­лять среднюю минимальную мощность накачки <Р_т> = = (W_p}NgVhvp_t где усреднение производится по объему актив­ной среды. Таким образом, можно написать

4_p = (W_p)N_eVhv_pJP; (3.1)

здесь средний КПД Для импульсного лазера по

аналогии имеем

t\_p = N_sVhv_p\(W_p)dt/E, (3.1 а)

где интеграл по времени берется в пределах от начала до конца импульса накачки, а Е — электрическая энергия, подведенная к лампе.

Следует заметить, что процесс накачки лазера можно рас­сматривать состоящим из четырех различных этапов: 1) испу­скания излучения от лампы, 2) переноса этого излучения к ак­тивному стержню, 3) поглощения его в стержне и 4) передачи поглощенной энергии верхнему лазерному уровню. Следова­тельно, КПД накачки можно записать в виде произведения

четырех членов, а именно

Лр^ЛгЛ/ЛаЛр?» (3.2) где цг — излучательная эффективность лампы, т. е. эффектив­ность преобразования электрической энергии на входе в оптиче­ское излучение на выходе в диапазоне длин волн, соответствую­щем полосам накачки лазерной среды (см., например, рис. 3.5,6); гр — эффективность передачи, которую можно оп­ределить как отношение мощности (или энергии) накачки, дей­ствительно поступающей в лазерный стержень, к мощности (или энергии), излучаемой лампой в полезном диапазоне длин волн накачки; ц_а — эффективность поглощения, т. е. доля света, попадающего в стержень, которая действительно поглошается средой; у]^- квантовый выход мощности (или энергии) иакач-

^{ки, т. е. доля поглощенной мощности (или энергии), которая}

приводит к созданию инверсии населенностей на верхнем уровне. В следующих разделах приводятся конкретные выражения для четырех членов, входящих в (3.2).

3,2.2. Излучательная эффективность и эффективность передачи1)

Согласно определению ц_Г| данному в предыдущем разделе, для непрерывной лампы можно написать следующее выра­жение:

Кг -

^{Чг = иг-$ 'а А, (3.3)}

где R — радиус, а / — длина лампы, /_х — ее спектральная интен­сивность, К\ и %2 — пределы диапазона полезного излучения, а

Р— электрическая мощность, подводимая к лампе. Для им­пульсной лампы выражение (3.3), очевидно, следует заменить на следующее:

Кг

Пг = пгЧ E_had\\ (3,3а)

я,

здесь *\ — спектральная плотность энергии, испускаемо " лам­пой в единичную площадь поверхности. Подробный расчет, ос­нованный на характеристиках излучения лампы, показал, что для типичных импульсных ламп, используемых для накачки им­пульсных лазеров на кристаллах Nd : YAG (в диапазоне 0,35— 0,9 мкм) и александрита (в диапазоне 0,35—0,7 мкм), ц_г « 0,43 и 0,36 соответственно. В случае Nd : YAG-лазера при накачке

непрерывной криптоновой лампой (т. е. для излучения в диапа-

Этот раздел можно было бы опустить для первого чтения.

зоне 0,7—0,9 мкм) значение ц_г несколько меньше, чем предыду­щее (т1г«0,27). Следовательно; в обоих случаях более 50% электрической мощности теряется либо в виде излучения, не по­падающего в полосы накачки, либо в виде теплоты, рассеянной на электродах. Следует заметить, что в соответствий с (3.3) h можно записать в виде

_1%

2nRl

(3.4)

^{нормированная плотность интенсивности}

_{(т. е. такая, что \%х<а=П- Выражение (3.4) позволяет}

•Hi /

о.

Si

% 0,8

напыленные rtsmmu поли рова иные

I о,

if

<ъ 0.6

_ад

lor

прокалибровать интенсивность /_х, если известны некалиброван-ный спектр испускания и излучательная эффективность лампы.

Прежде чем проводить вычисления эффективности передачи, уместно сделать несколько замечаний по поводу поглощения как стенками осветителя, так и плазмой лампы. На рис. 3.7 представлены кривые коэффициента отражения зеркальных по­верхностей, которые наиболее часто применяются на практике. Из рисунка мы видим, что напыленное серебро обеспечивает наибольший коэффициент отражения (-0,98) во всем интере­сующем нас спектральном диапазоне. Для полированного или нанесенного гальваническим способом серебра кривая циента отражения располагается несколько ниже, чем рассмот- ренная здесь (коэффициент отражения составляет около 0,94). Однако незащищенное серебро страдает от что пред-

ставляет собой серьезную проблему; следовательно, отража­тельная способность серебра со временем падает, поэтому сереб­ро иногда используют вместе с защитным прозрачным покрыти­ем, и то только в тех случаях, когда необходимо достигнуть

наиболынего КПД. Золотое покрытие обеспечивает практиче­ски ту же отражательную способность, что и серебро, но на длинах волн, превышающих примерно 0,65 мкм. Поскольку это покрытие намного более устойчиво к воздействию посторонних химических веществ, чем серебро, его применение, по-видимому,

^{разумно для непрерывного Nd: YAG-лазера, когда наибольшая}

часть излучения лампы приходится на длины волн, большие чем 0,7 мкм. Алюминий и медь из-за своей невысокой отража­тельной способности редко используются для покрытия освети­теля. Наконец, следует заметить, что хороший белый рассеива-тель (такой, как порошок BaS0₄ или белая керамика) обеспе­чивает диффузную отражательную способность, которая почти равна зеркальной отражательной способности серебра. Чтобы

получить некоторое представление о степени прозрачности плаз­мы импульсной лампы для ее собственного излучения, на рис. 3.8 представлено пропускание слоя ксеноновой плазмы тол­щиной 1 см для разных длин волн в зависимости от плотности тока лампы. Видно, например, что в основных-полосах накачки ионов Nd³⁺ (%> 0,6 мкм) при типичных для импульсной лампы плотностях тока (2000—3000 А/см²) плазма почти непрозрачна для собственного излучения. В действительности ослабление излучения несколько меньше, чем показано на рис. 3.8, по­скольку диаметр лампы обычно меньше, чем 1 см (как прави­ло, 5—6 мм). Тем не менее в дальнейшем рассмотрении будем считать в первом приближении, что плазма типичной импульс­ной лампы непрозрачна для собственного излучения. В случае же непрерывной лампы плотности тока (~ 150 А/см²), как

правило, много меньше приведенных выше значений и, следова­тельно, плазма лампы в значительной степени прозрачна для собственного излучения.

Сделав эти предварительные замечания, перейдем теперь к расчету эффективности передачи r\_t. Вначале рассмотрим слу­чай эллиптической полости осветителя (рис. 3.9). В этом случае r]t можно найти с помощью относительно простых геометриче­ских соображений [5]. Рассмотрим произвольную точку Р на поверхности осветителя, расположенную на расстоянии 1$ от центра стержня и на расстоянии U от центра лампы. Пусть

Длина ва/гпь:

О, в лтм 0,8 jtikm^

_та

зависимости от

а — угол между главной осью эллипса и радиус-вектором, со­единяющим центр лампы с точкой Р (рис. 3.9), а 9 — соответ­ствующий угол между этой осью и радиус-вектором, выходя­щим из центра стержня. Вес лучи, приходящие от лампы к точ­ке Я, заключены в конусе РАВ (рис. 3.9). Вследствие равенства углов падения и отражения эти лучи отображаются в конус РА^/В^/ вокруг стержня, где А'В' = ABl_R/l_L. Поскольку расстоя­ние А'В^Г зависит от отношения U/Il, нетрудно заметить, что часть эллиптического отражателя, расположенная ближе к лам­пе, формирует в месте расположения лазерного стержня увели­ченное изображение лампы, в то время как часть отражателя, расположенная ближе к стержню, формирует уменьшенное изо­бражение лампы. Поэтому существует такая точка Ре, для ко­торой расстояние А⁹ В' равно диаметру стержня 2R_R. Если ао и Оо — соответствующие угловые координаты точки Pq_} то видно, что при а < ао все лучи от лампы попадают внутрь стержня, в то время как при а > ао доля таких лучей составляет

(ЯА)/(*Л).^гД^{е 2r}l ^{и 2}^ Л'ВЪаким об-

разом, эффективность ' передачи для части осветителя, соответ­ствующей а < ао, дается следующим простым выражением:

О

_{а для а ао мы имеем}

Однако поскольку Wa = —/«^9, выражение (3,6) нетрудно проинтегрировать, и из (3.5) и (3.6) мы получаем следующее выражение для эффективности передачи \ = tj, + x\_t\

Дальнейшее развитие теории можно продолжить, если предпо­ложить, что лампа является абсолютно непрозрачной для соб­ственного излучения. При этом лампа будет поглощать любой свет, который после испускания лампой отражается эллиптиче­ским зеркалом обратно к лампе. Следовательно, в этом случае любые лучи, составляющие угол 0 < 8i (угол (К также указан на рис. 3.9), не попадут на стержень. Таким образом, мы имеем

ri, =^ [«о + (во — • (3.8)

Углы ао, 0о и 01 можно теперь выразить через диаметры стержня и лампы, а также через большую а и малую Ъ полу­оси эллипса. Конечный результат представлен графически на рис, ЗЛО, на котором верхняя группа кривых относится к слу­чаю, описываемому выражением (3.7), а нижняя группа дает

величину 91 /л;. Чтобы получить эффективность передачи в соот­

ветствии с выражением (3.8), последнюю величину следует умножить на Rr/Rl и затем вычесть из соответствующей орди­наты верхней кривой. Для получения численной оценки рас* смотрим эллиптическую полость с большой осью 2а — 34 мм и малой осью 2Ь = 31,2 мм и предположим, что 2Rr = 6,3 мм, a 2Rl = 4 мм. При этом из рис. ЗЛО получаем t]t & 0,9 или y\t ж 0,8 в зависимости от того, прозрачна или непрозрачна лампа для собственного излучения, т. е. в зависимости от того, используется ли для вычислений выражение (3.7) или (3.8).

0,2 0,3 ОЛ 0,5 О, в 0,7 0,8 0,9 ?,0

Ь/а

Рис 3,10. Эффективность передачи эллиптического осветителя. Набор верх­них кривых соответствует случаю, когда лампа прозрачна для собственного излучения. Для непрозрачной лампы поправки к эффективностям передачи получают с помощью нижнего набора кривых. (Согласно работе [5].)

Прежде чем закончить рассмотрение эллиптической полости, необходимо сделать два замечания. Первое состоит в том, что при записи формулы (3.5) мы косвенным образом предположи­ли, что лампа излучает одинаково в любом направлении а. Второе замечание связано с тем, что мы пренебрегли учетом того обстоятельства, что коэффициент отражения осветителя меньше единицы. Однако для серебряного покрытия (или зо­лотого, как в случае непрерывного Nd : YAG-лазера) обуслов­ленное этим уменьшение КПД является незначительным.

Вычислим теперь эффективность передачи для случаев на­качки, изображенных на рис. 3.1, а и е. В отличие от эллипти­ческого зеркала ни в одном из этих случаев осветитель не работает как концентрирующее свет зеркало, и поэтому здесь не­обходимо рассмотреть другой метод расчета. Простейшую оцен­ку в данных случаях можно получить, если предположить, что

интенсивность света / в полости является изотропной [6J. По­скольку все поверхности будут освещены светом одинаковой интенсивности, поглощающая способность каждой поверхности будет пропорциональна просто произведению площади 5 этой поверхности на ее относительную поглощающую способность ц. При этом мощность излучения, поглощаемая стержнем, дает­ся выражением

р_а = r\JS_Mt (3.9)

где ц_а — поглощающая способность стержня, a Sr — площадь его боковой поверхности. Поскольку весь излученный свет дол­жен быть в конечном счете поглощен, мощность света, излучае­мого лампой Pi, должна быть равна

PL = (*\a +l\peSpe + /; (ЗЛО)

здесь Цр_С— относительная поглощающая способность, a S_pc — площадь поверхности осветителя, и rji, $l—соответствующие величины для лампы. Поскольку отношение Р_а и PL равно про­изведению ц_а на v\t, то из (3.9) и (3.10) получаем

" чА + V + чА •

что в этом случае зависит от и поэтому, строго говоря, коэффициент передаЧи нельзя рассматривать как не­зависимую величину. С целью получения численной оценки предположим, что гц ж 1 (полностью непрозрачная лампа), х\рс = 0,04 и ц_а ~ 0,2 (это имеет место для стержня из Nd: YAG; см. табл. 3.1). Спиральную лампу, изображенную на рис. 3,1, а, можно аппроксимировать кольцевой лампой с ра­диусом кольца, равным Rl. В этом случае имеем Si = 4nRil, Spc ж 2nRd и Sr = 2kRrI, где / — длина осветителя. Тогда из выражения (3.11) получаем

r\t » Rr/(Q>2Rr + 2,04/?_L). (3.12)

Поскольку отношение Rr/Rl равно, как правило, 0,3 Ч- 0,8, зна­чения т]* обычно располагаются в интервале 0,1-г-0,4. д_Ля плотноупакованной конфигурации, такой, как на рис. 3.1, в в предположении, что Rl = RR = R, мы имеем S/, = Sr = 2nRl и Spc ж (2п + 4)/?/. При этом из выражения (3.11) получаем tv ж 0,62.

В заключение этого раздела можно сказать, что примене­ние эллиптической полости позволит получить наибольшую эф­фективность передачи (около 80 %), использование же плот­ноупакованной конфигурации дает лишь ненамного меньшую

эффективность, в то время как эффективность конфигурации со

Iспиральной лампой во многих случаях оказывается существен- но меньшей. Последняя конфигурация по-прежнему представ- ляет интерес для высокоэнергетических лазеров, поскольку спи- ральные лампы могут выдерживать значительно более высокие I входные энергии.

3.2.3. Распределение света накачки¹*

Для того чтобы вычислить долю падающего света накачки, поглощаемую активным стержнем, необходимо знать распре­деление этого света в активной среде. В данном разделе такое распределение будет рассмотрено для нескольких характерных случаев. Мы увидим, что оно во многих случаях является неодно­родным.

В качестве первого примера рас­смотрим стержень с полированной

боковой поверхностью. Предполо­жим также, что стержень накачи­вается либо спиральной импульсной лампой (рис. 3.1,а), либо линей­ной лампой в плотноупакованной конфигурации (рис. 3.1, в) или в эллиптическом отражателе с ма­лым эксцентриситетом, причем диа­метр лампы превышает диаметр

стержня. Во всех трех этих случаях можно считать, что свет падает на стержень, скажем, в точке Р (рис, 3.11) под любым углом в пределах я рад, как показано на рисунке. Кроме того, поскольку коэффи­циент преломления стержня обычно больше, чем коэффициент преломления окружающей среды, свет накачки, попав в стержень, стремится концентрироваться ближе к оси стержня. Это нетрудно понять, рассматривая два крайних луча 2 и 3, которые падают под углом я/2 к нормали относительно поверхности. Попадая внутрь стержня, эти лучи преломляются и становятся лучами 2' и 3', причем угол 6 является углом преломления. Если среда, окружающая стержень, представляет собой воздух, то sin 9 = Следова­тельно, все лучи, приходящие от лампы, будут преломляться в пределах угла 26 между лучами Т и 3'. Применяя такое же

⁴> Этот раздел можно пропустить при первом чтении.

самое рассуждение ко всем точкам Р поверхности S, мы при­ходим к выводу о том, что внутренняя часть стержня (радиусом R/n) накачивается более сильно, чем его внешняя часть. Вы­числение плотности энергии накачки р в стержне существенно упрощается, если 1) рассматривать свет, падающий на стер­жень только в плоскости, перпендикулярной его оси, и 2) пре­небрегать ослаблением интенсивности этого света по мере его

распространения в стержне. Тогда плотность энергии р_п в точке, расположенной вну­три стержня на расстоянии

г от его оси, равна [7]

р„ =п²р (0<г <R/n), (3.13) р„ = (2п²/я)р arcsin (R/nr) (R/n< г < R);(3.U)

здесь р — значение, которое плотность энергии имела бы в той же самой точке стерж­ня, если показатель прелом­ления был бы равен еди­нице. Эта плотность связа­на с интенсивностью излу­чаемого лампой света выра­жением (2.21). Если упро­щающих допущений 1) И 2)

^{не делать, то выражение}

для о_я оказывается значи­тельно более сложным [8].

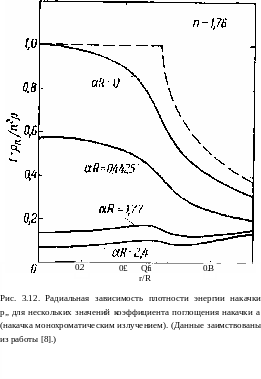
На рис. 3.12 приведены полученные расчетом кривые безразмер­ной величины

/ (aR, rjR) = p„M> (3-15)

для нескольких значений величины aR, где а — коэффициент

поглощения на длине волны накачки (предполагается, что на­качка представляет собой монохроматический свет). На этом же рисунке приведена также штриховая кривая, построенная в соответствии с выражениями (3.13) и (3 14). Следует обра­тить внимание на различие между штриховой кривой и сплош­ной кривой, соответствующей aR = 0. Хотя обе кривые отно­сятся к случаю, когда поглощение в стержне отсутствует,

сплошная кривая в отличие от штриховой учитывает то, что свет может входить в стержень под любым углом. Заметим так­же, что если aR ф 0, то благодаря ослаблению' интенсивности

света накачки по мере его распространения внутрь от поверх­ности стержня распределение плотности энергии р_п сглаживает­ся. Из рис. 3.12' следует, что в центре стержня (г = 0) величи­на f(aR, 0) может быть с хорошей точностью аппроксимиро­вана выражением /= ехр (—1,1а/?).

Тот факт, что для очень малых значений aR плотность энер­гии в центральной части стержня равна га²р, заслуживает не­сколько более подробного рассмотрения. Предположим, что лампа имеет такой же радиус, что и стержень, и расположена вдоль фокальной оси F_l (см. рис. ЗЛ, б). Поскольку на рис. 3.11 лучи 2 и 3 касательиы к поверхности 5, они должны соответ­ствовать двум лучам, касательным к поверхности лампы. После преломления лучи 2 и 3 становится лучами 2' и 3', которые ка­саются окружности радиусом R/n. Следовательно, можно ска­зать, что стержень действует как цилиндрическая линза, фор­мируя изображение лампы в своем центре, которое в п раз меньше истинного размера лампы. Поскольку объем, занимае­мый этим изображением, в п² раз меньше объема лампы, можно понять, почему соответствующее значение плотности энергии рп увеличивается в п² раз.

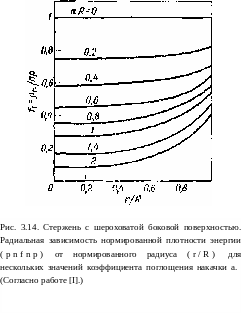
Мы уже показали, что при очень небольших значениях aR плотность энергии накачки однородна лишь в центральной части стержня г < R/n_f я то время как вне этой области она неоднородна.'Очевидно, что неоднородное распределение плот­ности Энергии в активной среде является нежелательным. По­лучить однородное распределение можно [7], если активный стержень поместить в цилиндрическую оболочку из прозрачно­го материала с тем же показателем преломления, что и у стержня (рис. 3.13). В этом случае, если радиусы лампы и обо­лочки сделать одинаковыми и равными nR_y то можно повторить рассуждения с помощью рис. 3.11, начиная с анализа хода лу­чей через точку Р, расположенную на поверхности оболочки. В этом случае преломленные лучи 2^/ и 3' будут касаться по­верхности активной среды и внутри нее будет собираться весь падающий свет. Если aR = 0 и свет проникает в среду только в плоскости рис. 3.13, то плотность энергии в активной среде становится однородной и определяется выражением (3.13). Дру­гой способ, который позволяет получить более однородную на­качку, состоит в матировании боковой поверхности В этом случае свет накачки, попадая на поверхность стержня, будет рассеиваться, и, следовательно, он не будет концентри­роваться, как на рис. 3.11. На рис. 3.14 построены кривые за­висимости от r/R безразмерной величины

fi (aR, r/R) = p_n/np_t

(3.16)

_I

■I

!

126 8. Процессы накачки

полученные для рассматриваемого случая путем расчета при нескольких значениях aR [1]. Здесь, как и прежде, а — коэф­фициент поглощения на длине волны накачки (для монохрома­тического света накачки). Заметим, что при aR ~ О мы имеем р_п = пр. Множитель п возникает в этом случае вследствие того, что скорость света в стержне в п раз меньше, чем скорость света в вакууме [см. (2.21)]. Таким образом, предполагается,

что при данном излучении лампы плотность энергии р_п в п раз превышает значение величины р, которое эта величина имела бы, если бы показатель преломления стержня равнялся единице. Из рис. 3.14 следует, что в центре стержня величину fx (aR, 0) можно с хорошей точностью аппроксимировать выражением fx » ехр(—1,27 aR). Сравнение выражений (3,16) и (3.15) при rj = 0 показывает, что, за исключением небольшого различия между функциями / и Д, шероховатость боковой поверхности стержня действительно приводит к уменьшению плотности энер­гии накачки в его центре в п раз. Однако теперь более или ме­нее однородно освещается все сечение стержня, а не только его ядро радиусом R/n. В самом деле, с помощью рис. 3.12 и 3.14 можно показать, что в обоих этих случаях интегральная плот­ность энергии накачки по сечению стержня приблизительно одинакова.

Рассмотрим теперь случай, когда радиус RL лампы меньше, чем радиус R% стержня. Пусть система накачки имеет ту же

конфигурацию, что и на рис. 3.1,6. Если боковая поверхность стержня полирована, то в стержне будет формироваться эллип­тическое изображение лампы. Это можно понять с помощью рис .3.15, на котором изображена лампа с боковой поверхностью Sl, расположенная вдоль фокальной оси F_x эллиптического ци­линдра. Форму изображения лампы, создаваемого эллиптиче­ским отражателем на второй фокальной оси F₂, можно полу­чить, рассматривая лучи, испукаемые касательно к поверх­ности лампы. Отражаясь от поверхности эллиптического ци­линдра, эти лучи преобразуются в пучок лучей вокруг второй фокальной оси F₂. Огибающая этих лучей представляет собой поверхность Si и является изо­бражением лампы, сформирован­ным эллиптическим цилиндром. На рис. 3.15 показаны те лучи, которые ограничивают поверх­ность S'_L в горизонтальном и

вертикальном направлениях, Очевидно, что изображение Si

вытянуто вдоль малой оси эл­липтического отражателя. В дей­ствительности можно показать,

эллиптического цилиндра.

^{что само изображение является}

эллипсом. На рис. 3.15 с по­мощью простых геометрических

соображений можно найти большую Rm и малую Rm оси этого эллипса. Если предположить, что радиус Ri лампы много меньше, чем малая ось эллиптического отражателя, то для Rm и R_m можно получить следующие выражения:

(3.17а) (3.176)

где е — эксцентриситет эллиптического отражателя. В дей­ствительности из-за преломления на поверхности стержня, ко­торая вновь действует как цилиндрическая линза, большая и ма­лая оси этого изображения уменьшаются в п раз по сравнению с приведенными выше значениями. Чтобы избежать неоднород­ного распределения накачки, которое возникает в процессе фор­мирования изображения, боковую поверхность можно сделать грубо шероховатой.

Представленное выше рассмотрение относится только к слу­чаю, когда стержень окружен воздухом (п=1). Однако во многих случаях стержень необходимо охлаждать, для чего его помещают в какую-либо жидкость, которой является обычно вода. В этом случае в проведенное выше рассмотрение необхо­димо внести некоторые изменения. В частности, у стержня с полированной боковой поверхностью радиус ядра, в котором концентрируется максимум энергии накачки, равен не RJn_f как на рис. 3.11, а Кщ\п, где щ — показатель преломления окружаю­щей жидкости. Для стержня же с шероховатой боковой поверх­ностью присутствие жидкости стремится свести на нет эффект матирования боковой поверхности. Поэтому распределение

^{энергии накачки оказывается значительно менее однородным,}

чем то, которое показано на рис. 3.14. Это особенно верно для эллиптического цилиндра благодаря тому, что неоднородность

распределения здесь обусловлена особенностями формирования

изображения (см. рис. 3.15). В заключение можно сказать, что плотноупакованная конфигурация системы накачки, изображен­ная на рис 3.1,6, в случае, когда поверхность стержня грубо отшлифована, а осветитель дает либо зеркальное, либо диф­фузное отражение, обеспечивает наиболее однородное распре­деление энергии накачки внутри стержня. Однако по сравнению с эллиптическим цилиндром эффективность передачи здесь не­сколько ниже, в то время как в конфигурации со спиральной лампой, когда имеет место однородное распределение энергии накачки по всему стержню, она существенно выше. В качестве последнего замечания в данном разделе укажем на то, что при­веденное выше рассмотрение справедливо для монохроматиче­ского излучения накачки. Для полихроматического же излучения выражения (3.14) — (3.1.6), а также кривые на рис. 3.12 и 3.14

остаются справедливыми, однако и р заменяются на соответ­ствующие спектральные величины р„\ и р?..

3.2.4. Эффективность поглощения и квантовый выход накачки '< [9]

Согласно определению эффективности поглощения г\_а, дан­ному в разд. 3.2.1, можно написать следующее выражение:

■n = PJP. = [ [ (dPJdV)dVd% LiS,,dk,(3.lH)

_{к v и}

где P — полная мощность, поглощенная стержнем, a dP%fd V — поглощенная мощность на единичный интервал длин волн и на единичный объем, Р_е — полная мощность излучения, падающего

¹⁾ Этот раздел можно опустить при первом чтении.

на стержень, и h% — соответствующая интенсивность на еди­ничный интервал длин волн; Sr — площадь боковой поверхности стержня. В выражении (3.18) объемный интеграл вычисляется по всему объему активной среды, а интеграл по длине волны — по полезному диапазону излучения лампы. С помощью выраже­ний (1.10) и (2,137) при / = сор/п величину dPг_t/dVмoжкo за­писать в виде

dPJdV = W_p% N_ghv = (с₀/п) aN_g р_яХ, (3.19)

где ""_Рх " — скорость накачки для излучения в диапазоне длин волн между Я и К+ dk. Как особенно характерный пример, рас­смотрим случай, когда боковая поверхность стержня шерохова­тая. Тогда с помощью (3.16) и (2.22) выражение (ЗЛ9) можно переписать следующим образом:

dPjdV = 4oN_g f_xl_eX. (3.20)

Используя (3,20), выражение (3.18) можно переписать как

^{ть = И ^N^UdVdXJS}_r^{\udh. (3.21)}

v к I X

Предположим, что эффективность передачи не зависит от дли­ны волны, так что мы имеем I_e% ~ gx> где g% — нормированное излучение лампы [см. (3.4)]. Определим также среднее значе­ние величины fi как(Z^) = (l/V)\ fi dV, где V — объем стержня.

Вспоминая затем, что \ g_kdX—I, получаем особенно простое

А»

^{выражение для}

_{r|a =-|^" J} ^a_{(f\)ё% dh = J 2aRR <|,> gK dX, (3.22)}

^R Л Я

где Rr — радиус стержня и а — коэффициент поглощения активной среды на данной длине волны. Заметим, что в соот­ветствии с выражением (3.22) ц_а — это просто среднее значе­ние безразмерной величины 2oi?/?</.>, полученное усреднением по спектральному распределению излучения лампы g_x. Посколь­ку в хорошем приближении </_t> « ехр[— (aR_R)\ (см. зада­чу 3.3), мы имеем

^у\_а ^{— {2aR}_R ^{ехр [- (а#}_я^{)] >; (3.22а)}

здесь усреднение производится по спектральному распределе- нию лампы

Прежде чем вычислить квантовый выход мощности накач- ки заметим, что (dP_x/dV)/hvпредставляет собой число

5 О. 3 вел то

атомов (в единичном o6beMevна единичный интервал длин волн), переведенных из основного состояния в полосу накачки с дли­ной волны около К (Y - соответствующая частота). Определим квантовый выход накачки %(Х) (не путайте с ц_рд) как отноше­ние числа атомов, которые релаксируют на верхний лазерный уровень, к числу атомов, которые заброшены в полосу накач­ки вблизи данной длины волны К. При этом мощность, которую можно снять (в единичном объеме и единичном интервале длин волн) на верхнем лазерном уровне, будет равна t]_qhv_p (dP'J

fdV)/hv. Тогда квантовый выход мощности накачки можно за­писать в виде

^ ^ (dPJhv dV) T)>v dV d%

Лр_Я = ^{V K} _r r • (³-²³)

V \ (dPJdVdV dK

V к

Используя (3.20) и вновь предполагая, что h% ~ gi, выраже­ние (3.23) можно свести к достаточно простому виду:

_Sw%K(f.))^

Ч_И = - г • (3-24)

А

Отсюда видно, что x\_pq выражается через безразмерную вели­чину (йД_р)%, усредненную по функции cigx<fi> « ^ а^ехр(—aRx)_y т. е.

_Црд = {(Х/Хр) т|Д (3.25)