2.9.4. Квантовомеханический расчет вероятностей

^{излучательного перехода}

Чтобы придать нашим рассуждениям более количественный характер, рассмотрим здесь кратко квантовомеханический расчет вероятности перехода W. Упрощенное рассмотрение ис- пользуется просто для того, чтобы показать, каким образом по- лучаются правила отбора. Вероятность перехода можно предста- вить выражением (2.39), при условии что нам известно значе- ние величины колеблющегося дипольного момента Прежде чем вывести выражение для |р.|², вспомним, что для ансамбля отрицательных зарядов (электроны молекулы) величиной е (с учетом знака) и положительных зарядов величиной е_н (ядра молекулы) классический электрический дипольный момент ра- вен ji = Y*i^evi-\- Здесь г, и R/ определяют положения соответственно электронов и ядер относительно некоторой точ- ки отсчета, а суммирование производится по всем электронам и

ядрам молекулы. Если за точку отсчета принять центр положи­тельных зарядов, то R; = 0и \*> принимает вид

ti=Y_ier_i. (2 Л 78)

i

Для простоты будем теперь рассматривать двухатомную моле­кулу, В этом случае координаты ядер можно описать величиной R межъядерного расстояния R и угловыми координатами в и ф радиус-вектора R относительно данной системы отсчета. Тогда в соответствии с квантовой механикой колеблющийся диполь­ный момент молекулы дается выражением [см. также (2.33)]

М₂, = 2Re ^ 1$>2(г., /?, г_г)(г., R, r_r)dr_idRdv_r, (2.179)

где i|>2 и — волновые функции соответственно конечного и на­чального состояний перехода. Заметим, что как tb_b так и яЬ₂ являются функциями координат всех электронов, межъядер­ного расстояния R и вращательных координат t% (сокращенная запись для 6 и Ф)> причем интегрирование производится но всем этим координатам. В соответствии с приближением Борна-Оппенгеймера молекулярные волновые функции -ф можно запи­сать в виде

Wi> R> r_r) = «_е fa, R)u_v (R)u_r (г_г) exp [— / (£/Щ (2.189)

где и_е> Uv и и_г — соответственно электронная, колебательная и вращательная волновые функции, а Е — Е_е + E_v + Е_г — полная энергия данного состояния. Из (2.179) и (2.180) нетрудно пока­зать, что М₂₁ колеблется с частотой v₂i= (E.₂ — E_{)/h с комп-

лексной амплитудой (2.28) ] определяемой выражением

_с

(2.181)

X «J X X О r

где

)i_e(R) =[&,(r_i,R)pLU_Jtl(r_t,

flWty,

(2.182)

здесь дипольныи момент, определяемый выражением

(2.178). Поскольку электронные волновые функции являются медлеиноменяющимися функциями расстояния /?, ц_с(/?) можно разложить в степенной ряд в окрестности равновесного межъ­ядерного расстояния Ro'-

_{МЯ) = М*о) +-тпг (Я -До) + ... • (2.183)}

_i

В случае чисто вращательных переходов и_2е — Щ_е и и₂? = = U\_v. При этом из (2.182) видно, что дипольный момент

_{МЛо) Р}^авен

^{М*а) = Ы«1«(Гь W^- (2.184)}

и является постоянным электрическим дипольным моментом Цер молекулы. Из (2.181), если положить jn_e ^jte(#o) и учесть,

что ^ u_2vu_lvdR — ^\ u_lv р dR — \, мы получаем следующее выра­жение для ' (л)" = ||А21|², которое можно использовать в (2.39):

| ц F = | fi_ep |²1 $ u\_Tu_XT dr_r I². (2.185)

Первый множитель в правой части этого выражения указывает на то, что чисто вращательные переходы возможны только в мо­лекулах, обладающих постоянным дипольным моментом |л_ср-Это нетрудно объяснить, поскольку в случае, скажем, спонтан­ного испускания излучение можно считать обусловленным вра­щением рассматриваемого дипольного момента. Для молекул с постоянным дипольным моментом величина | f 11² пропорцио­нальна при этом второму множителю, стоящему в правой части выражения (2.185). Из свойств симметрии вращательных волно­вых функций следует, что этот множитель отличен от нуля толь­ко тогда, когда изменение вращательного квантового числа Д/ между двумя состояниями подчиняется правилу отбора Д/ =

_{= =Ы.}

В случае вращательно-колебательных переходов мы снова имеем щ_е = Щ_е и, следовательно, в первом приближении опять можем записать \х_е [R) ж \х_е (Ro) — Цер. Если ц_ер подставить

в (2.181), то JUL2 1 сводится к выражению (м-_ер\ ^W2u^ly

X которое за счет ортогональности колебатель-

ных волновых функций, принадлежащих одному и тому же элек­тронному состоянию, равно нулю. Поэтому в разложении (2.183) необходимо учесть второй член, который после подстановки в (2.181) дает следующее выражение для |ц,|²:

рг₂ j ¹⁹ =

2с 2 Г |2

^{- - ~ (2.186)}

Третий сомножитель в этом выражении вновь дает правило от­бора А/ = ±1 для изменения вращательного квантового числа. Что касается второго сомножителя, то если кривую потенциаль­ной энергии U(R)аппроксимировать параболой (упругая сила), то волновые функции и„ будут представлять собой хорошо известные функции гармонического осциллятора, т. е. произведе­ние полиномов Эрмита и гауссовой функции. Учет свойств сим­метрии этих функций, приводит к тому, что ji₂1|² оказывается отличным от нуля лишь при Ао = ±1. Обертоны появляются тогда, когда предположение о иараболичности кривой потен­циальной энергии оказывается неверным (ангармонизм потен­циальной энергии) или когда учитывается следующий член бо­лее высокого порядка в разложении (2.183) (электронный ан­гармонизм). Наконец» заметим, что при определенных условиях симметрии нулю может быть равен первый множитель в (2.186). Например, это имеет место, когда два атома являются тожде­ственными (скажем, в молекуле N₂ одного изотопного состава), Действительно, в данном случае вследствие симметрии моле­кула не может иметь дипольного момента \x_e{R)- При этом в выражении (2.186) |ц]² всегда равно нулю, и переход назы­вается неактивным в ИК-области.

В завершение изучим случай вибронных переходов, Если в разложении (2.183) рассматривать лишь первый член, то в со­ответствии с (2.181) мы имеем следующее выражение:

^ (#о) |²1 \ ^ulu^uiv ^dRf\\ ^ulr^u\r ^drr f • (2.187)

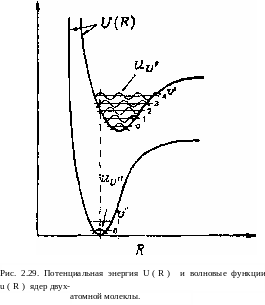
Третий сомножитель в правой части этого выражения снова приводит к правилу отбора AJ = ±1. Если первый сомножитель в (2.187) равен нулю благодаря свойствам симметрии элект­ронных волновых функций, то такой вибронный переход назы­вается электродипольно запрещенным. Для разрешенного пере­хода величина |fi)², а следовательно, и вероятность перехода W в данное колебательное состояние оказываются пропорциональ­ными второму сомножителю в выражении (2.187), известному как множитель Франка — Коидона. Заметим, что в рассматри­ваемом случае этот множитель отличен от нуля, поскольку u_2v и u\_v принадлежат различным электронным состояниям. Таким образом, вероятность перехода W определяется степенью пере­крытия волновых функций ядер. Рассмотрим случай, представ­ленный на рис. 2.29, где колебательные уровни основного и воз­бужденного электронных состояний обозначены соответственно символами v" и v'₉ и предположим, что молекула первоначаль­но находится на основном колебательном уровне v" = 0. При этом видно, что наибольшей является вероятность перехода в возбужденное состояние с v^f= 4, для которого мы имеем мак­симальное перекрытие между волновыми функциями ядер u_v» и u_v<. Таким образом, принцип Франка - Кондона, который мы ввели выше для качественного рассмотрения, представлен теперь в более точной и количественной форме.

Основываясь на проведенном выше анализе, можно сделать следующие выводы относительно правил отбора, которые при­менимы к излучательным переходам; 1) для Чисто вращатель­ных переходовв и для молекул, обладаЮщих постоянным ди-польным моментом, ■ вероятность перехода определяется прави­лом отбора М = ±1 для

изменения вращательного

состояния (для более слож­ных молекул возможно так­же Д/ = 0). 2) В случае ак­тивных в ИК-области вра-щатсльно-колебательных пе­реходов вероятность пере­хода определяется прави­лом отбора Д/ = ±1 для

^{изменения вращательного}

состояния (или также А/ = = 0) и До = ±1 для изме­нения колебательного со­стояния (возможны также обертонные переходы с Ди = ±2, ±3, но они значи­тельно более слабые). 3) Для диполыю-разрешенных вибронных переходов веро­ятность перехода в данное вращательно-колебательное состоя­ние определяется величиной множителя Франка - Кондона для изменения колебательного состояния и правилом отбора Д/ = ± 1 (или также Д/ — 0) для изменения вращательного состояния.

_Задачи

2.1. Для полости объемом К= 1 см^а волн в пределах полосы шириной = 600 им.

определите число мод, имеющих длины АХ = 100 А с центром в точке Я«

2.2. Длина волны Кки соответствующая максимуму распределения на рис. 2.3, удовлетворяет соотношению ХуТ = 2,9*10~³ м - К (закон смещения Вина). Вычислите Км при Т = 6000 К. Какой цвет соответствует этой длине волны?

2.3, Линия лазерного перехода fti рубина хорошо описывается лоренцевой криво!?, причем ее ширима на уровне 0,5 от максимального значения равна 330 ГГц (см, рис. 2.9). Измеренное значение сечения перехода в максимуме линии равно а = 2,5- Ю^-20 см², Вычислите изл у нательное время жизни (по- казатель преломления п = 1,76). Чему равен квантовый выход люминесцен- ции, если при комнатной температуре наблюдаемое время жизни равно 3 мс? * "

2.4. Во многих случаях типичной активной средой лазера является Nd : YAG. представляющий собой кристалл YjAlA, (иттрий-алюминиевый гранат,

YAG), в котором часть ионов Y³⁺ замещена ионами Nd³⁺. Обычно концентра­ция ионов Nd³⁺ составляет 1 ат. %, т.е. 1 % ионов Y³⁺ замещен ионами Nd^3!. Плотность кристалла YAG равна 4,56 г/см³. Определите концентрацию ионов Nd³¹, находящихся на основном уровне (V_9/2). В действительности этот уровень состоит из пяти (дважды вырожденных) уровней, из которых четыре верх них отстоят от нижнего на 134, 197, 311 и 848 cm~^j соответ­ственно. Вычислите концентрацию ионов Nd^3H", находящихся на самом низ­ком уровне состояния ^kh/%.

5. Лазерный переход в Nd : YAG хорошо описывается лоренцевой кривой с шириной порядка 195 ГГц (определяемой на уровне 0,5 от максимального значения) при комнатной температуре (см. рис. 2.9). Время жизни верхнего лазерного уровня t = 230 мке, квантовый выход люминесценции лазерного перехода составляет около 0,42, а показатель преломления YAG равен 1,82. Вычислите сечение перехода в максимуме линии.

6. В лазерном переходе неона на длине волны % = 1,15 мкм преобладает доплеровское уширение с шириной Д\<₀ = 9-10⁸ Гц. Время жизни верхнего уровня ~ 10~⁷ с. Вычислите максимальное значение сечения перехода, если время жизни лазерного перехода равно полному времени жизни верхнего состояния.

7. Квантовый выход перехода ->So (см. рис. 6.29) в красителе родамин 6С/ равен 0,87, а соответствующее время жизни ~5 не. Вычислите спонтан­ное т_Спонт и безызлучательное Тбезызл времена жизни уровня Si.

8. Вычислите доплеровскую ширину линии перехода с К = 10,6 мкм (Г = = 400 К) молекулы С0₂. Поскольку в С0₂-лазере столкновителыюе ушире­ние этого лазерного перехода составляет около 5 МГц/(мм рт. ст.), найдите, при каком давлении углекислого газа оба механизма дадут одинаковые вклады в ширину линии.

9. Вычислите однородную ширину линии перехода с % = 0,633 мкм в нео­не, если известно, что Av_eCr — 20 МГц, а Avc-голкк = 0,64 МГц [см. выраже­ние (2.66)]. Какую форму имеет результирующая линия?

10. Верхний уровень лазера на Nd : YAG в действительности состоит из двух сильно связанных подуровней, отстоящих друг от друга на Д£ — = 88 см*"¹ (см. рис. 6.2). Генерация происходит на переходе с подуровня R2 верхнего уровня на подуровень нижнего (⁴/ц/2) лазерного уровня. Сечение данного перехода равно 0 = 8,8- Ю^-12 см². Найдите эффективное сечение усиления лазерного излучения.

11. Цилиндрический стержень из Nd : YAG диаметром 6,3 мм и длиной 7,5 см накачивается мощной импульсной лампой. Значение сечения лазерного перехода в максимуме линии с длиной волны 1,06 мкм равно а = = 3,5- Ю~¹⁹ см², а показатель преломления равен п = 1,82. Найдите крити­ческую инверсию населенностей, соответствующую началу процесса усиления спонтанного (УСИ) (предполагается, что на оба торца лазерного стержня нанесены идеальные просветляющие покрытия, т. е. они не отра­жают свет). Кроме того, вычислите максимальное количество энергии, кото­рая может быть запасена в этом стержне, если необходимо избежать воз­никновения процесса УСИ.

12. Для модуляции добротности и синхронизации мод (см. гл. 5) рубино­вого лазера часто применяют раствор крнптоцианина (иодид 1,1'-диэтил-4,4^/-карбоциаиина) в метиловом спирте. Сечение поглощения криптоцнанина на длине волны излучения рубинового лазера (К = 0,6943 мкм) равно

8,1 • Ю^-16 см². Время жизни верхнего уровня т = 22* 10~¹² с. Определите интенсивность насыщения для этой длины волны.

13. Лазер на Nd : YAG (А, = 1,06 мкм) действует по четырехуровневой схеме. Сечение перехода в максимуме линии составляет а_р = 3,5-10^-19 см², а время жизни т = 0,23 мс. Вычислите интенсивность насыщения уси­ления.

14. В молекуле С0₂, находящейся в тепловом равновесии (Т = 400 К), мак­симум населенности на уровне (0, 0_t 1) (см. рис. 6.14) соответствует враща­тельному подуровню с квантовым числом /' = 21. Найдите для уровня (О, О, 1) молекулы СОа вращательную постоянную В.

15. Пользуясь результатами предыдущей задачи, определите разность ча­стот между вращательными линиями (рис. 2.28) лазерного перехода моле­кулы СОг с длиной волны X = 10,6 мкм (считайте, что вращательная по­стоянная одна и та же для верхнего и нижнего уровней и учтите, что благодаря правилам отбора в молекуле С0₂ вынужденное излучение испу­скается лишь с уровней с нечетными значениями квантового числа /).

16. При каком давлении должен находиться углекислый газ, чтобы все вращательные линии слились в одну? Какова при этом давлении ширина

линии усиления?

17. Вместо величины p_v можно также ввести спектральную плотность энергии ря» определяемую таким образом, что р% dX равна плотности энергии электромагнитного излучения с длинами воли от К до Я + dX. Найдите соот­ношение между р% и pv

18. Найдите максимум р*. в зависимости от К. Покажите, что длина вол­ны Xsu соответствующая максимуму рд„ удовлетворяет соотношению ХмТ = = he/ky (закон смещения Вина), где у определяется из уравнения 5[1 — ехр(—у)] = у. Найдите приближенное значение у из этого уравнения (у = 4,965).

19. Найдите соотношение между интенсивностью / и соответствующей плотностью энергии для плоской электромагнитной волны, сравните с выра­жением (2.21) и объясните различия.

20. Вместо того чтобы наблюдать насыщение по схеме рис. 2.15, можно проделать то же самое, пользуясь лишь одним пучком света /(v) и измеряя коэффициент поглощения для этого пучка. Покажите, что в этом случае для однородно уширенной линии коэффициент поглощения определяется следующим образом?

a/v-v₀) = - ^a°^№

I₊₄„-_(v_V_o)2_T2_+///s0'

здесь я₀(0)—коэффициент поглощения слабого сигнала (/«С I_so) на ча­стоте V = Vo, а Лчо — интенсивность насыщения, определяемая формулой (2.140), на частоте v = v₀. Указание: вначале покажите, что

а₀ (0) 1

_МО)

^{1 + 4л2 (v - v}₀^{)4r2 1 + (l/I}_m^{){l/[l + 4л:2 (v - v}₀^{)2 '}

2.21. Используя выражение, полученное в предыдущей задаче, найдите за­висимость коэффициента поглощения в максимуме линии и ширимы линии поглощения от интенсивности /. Как можно измерить интенсивность насы­щения I_sq?

2.22. Покажите, что для неоднородно уширенной линии, форма которой опи­сывается функцией g, коэффициент поглощения при насыщении, измеряемый по схеме рис, 2.15, можно записать в виде

/ 2я²

_х f 2x_cv'g* (У" - vq) <W_

J 1 + Ал (v — v^ff x\ 1 + (///₅₀) {l/[l + 4л (v' - v")² t? ]} '

где вклад от однородно уширенной линии описывается лоренцевым кон­туром. [Указание: начните с вычисления элементарного вклада в поглоще­ние da, обусловленного той частью g*(v" — vo)dv^r/ атомов, резонансные частоты которых лежат между v" и v" + dv".]

2.23. Считая, что однородная ширина линии много меньше неоднородной и что / < /_$0, покажите, что выражение для а, полученное в предыдущей задаче, можно приближенно записать в виде

2ат²

Г _/f dv^ }

^{1 Ho J [l+4n2(v/-vTr}_c^{2][l+4^(v^vT^] J'}

Учитывая, что входящий в данное выражение интеграл представляет собой свертку двух лоренцевых линий, определите ширину пропала, показанного на рис. 2.19.

2.24. На коротких длинах волн (ВУФ, мягкий рентген) преобладающим ме- ханизмом уширения является естественное уширение. Используя формулу

(2.116), покажите, что сечение в максимуме линии равно o§=ti§J2n.