
- •Isbn 5-03-001053-х (русск.) isbn 0-306-42967-5 (англ.)
- •1.1. Спонтанное и вынужденное излучение; поглощение
- •1.1.1. Спонтанное излучение (рис. L.Lf а)
- •1.1.2. Вынужденное излучение (рис. 1л?б)
- •1.2. Принцип работы лазера
- •1.3. Схемы накачки.
- •БН&лиогека вшшгездячшсогв институт з
- •1.4. Свойства лазерных пучков
- •1.4.1. Монохроматичность
- •1.4.2. Когерентность
- •1.4.3. Направленность
- •Электромагнитная Волна
- •1*4.4. Яркость
- •1.4.5. Импульсы малой длительности
- •1.5. Структура книги
- •2.1. Введение
- •2.2. Теория излучения черного тела [1]
- •2.3. Поглощение и вынужденное излучение
- •2,3.1. Вероятности поглощения и вынужденного излучения
- •2.3.3. Механизм уширения линии
- •2.3.3.1. Однородное ушарение
- •2.3.3.2. Неоднородное уширение
- •2.3,3.3. Выводы и примеры
- •2.3.4. Сечение перехода, коэффициенты поглощения и усиления
- •2.4, Спонтанное излучение
- •2.4 Л. Полуклассический подход
- •2.4.2. Квантовоэлектродинамический подход
- •2.4.3. Термодинамический подход Эйнштейна
- •2.4.4. Связь между спонтанным временем жизни
- •Ол *споит
- •2.4.5, Заключительные замечания
- •2.5. Безызлучательная релаксация [11]
- •2.6. Насыщение
- •2.6.1. Насыщение поглощения; однородно уширенная линия
- •2.6.3. Неоднородно уширенная линия
- •2.7. Релаксация многоатомной системы
- •2.7.1. Захват излучения
- •2.7.2. Сверхизлучение и суперлюминесценция
- •2,8. Вырожденные уровни
- •2.9. Молекулярные системы
- •2,9,1. Энергетические уровни молекул
- •2.9.2. Заселенность уровней при тепловом равновесии
- •2.9.3. Излучательные и безызлучательные переходы
- •2.9.4. Квантовомеханический расчет вероятностей
- •Литература
- •3.1. Введение
- •3.2. Оптическая накачка [1, 2]
- •3.2.1. Кпд накачки
- •3,2.2. Излучательная эффективность и эффективность передачи1)
- •3,2.5. Заключительные замечания
- •3.3. Электрическая накачка
- •3.3.1. Физические свойства газовых разрядов [10—12]
- •3.3.2. Возбуждение электронным ударом
- •3.3.2.1. Сечение электронного удара [13]
- •3.3.2.2. Распределение энергии электронов
- •3.3.2.4. Уравнение ионизационного равновесия
- •3.3.2.5. Вычисление скорости накачки
- •3.3.3. Возбуждение посредством (около)резонансной
- •3J1. Покажите, что упругие столкновения встречаются значительно более
- •3.12. Теория амбиполярной диффузии дает следующее соотношение между электронной температурой т„ и произведением pD:
- •Литература
- •4.1. Введение
- •4.2. Некоторые разделы геометрической и волновой оптики
- •4.2.1. Матричная формулировка геометрической оптики [1]
- •4.2.2. Интерферометр Фабри—Перо [2]
- •4.2.3. Многослойные диэлектрические покрытия [3, 4]
- •Падают пучок
- •Отраженный
- •4.3. Время жизни фотона и добротность резонатора
- •4.4. Плоскопараллельный резонатор
- •4.4.1. Приближенная теория
- •4.4.2. Теория Фокса и Ли
- •4,5, Конфокальный резонатор [8]
- •4.6. Распространение гауссова пучка
- •Волны (б).
- •4.7. Обобщенный сферический резонатор [8]
- •4.7.1. Амплитуды мод
- •4.7.2. Резонансные частоты и дифракционные потери
- •4.7.3. Условие устойчивости
- •1 Положительная
- •(Кпршщтщшт ветвь
- •Отрицательная йетвь
- •4.8. Неустойчивые резонаторы [14, 15]
- •4.8.1. Геометрическое описание
- •4.8.2. Описание с помощью волновой оптики
- •4.8.3. Достоинства и недостатки неустойчивых резонаторов
- •4.8.4. Неустойчивые резонаторы с переменным коэффициентом отражения
- •Литература
- •5Л. Введение
- •5.2. Скоростные уравнения [2, 3]
- •5.2.1. Четырехуровневый лазер
- •5.2.2. Трехуровневый лазер
- •5.3. Непрерывный режим работы лазера
- •5.3.1. Четырехуровневый лазер
- •5.3.2. Трехуровневый лазер
- •5.3.3. Оптимальная связь на выходе лазера [7]
- •5.3.4. Перестройка частоты генерации лазера
- •5*3.5. Одномодовая и многомодовая генерация
- •5.3S.L Причины возникновения многоходовой генерации
- •5.3.5.2. Одномодовый режим генерации
- •5*3.6. Два числовых примера
- •5.3.8. Провал Лэмба и активная стабилизация
- •5.4, Нестационарный режим работы лазера
- •5.4Л, Релаксационные колебания в одномодовых лазерах
- •5.4.2, Пичковый режим многомодовых лазеров
- •5.4,3. Модуляция добротности [21]
- •5.4.3.1. Методы модуляции добротности
- •Дисррскшрозиитт пучок
- •5.4.3.2. Режимы генерации
- •5.4.3.4. Числовой пример
- •5.4.4. Модуляция усиления
- •5.4.5. Синхронизация мод [26, 27]
- •5.4Mj. Методы синхронизации мод
- •Машцштшйсн поглотитель
- •5.4.5.2. Лазерные системы с сихронизацией мод
- •5.4.6. Разгрузка резонатора
- •Выходной пучок
- •Ахтпшная среда
- •Дифрагированные пучки
- •5.5. Заключительные замечания
- •Литература
- •5. Непрерывный и нестационарный режимы работы лазеров
- •6.2. Твердотельные лазеры
- •6.2.1. Рубиновый лазер [1]
- •6.2.2. Неодимовые лазеры [4—6]
- •6.2.2.1. Nd : yag-лазер
- •6.2X2. Стекло с неодимом [7]
- •6.2.3. Лазер на александрите [8]
- •6.3.1. Лазеры на нейтральных атомах
- •6.Зал. Гелий-неоновые лазеры
- •6.3.1.2. Лазеры на парах меди и золота [12]
- •6.3,2. Ионные лазеры
- •6,3.2.1. Аргоновый лазер [13, 14]
- •Метастабитные уровни
- •6.3.3. Молекулярные газовые лазеры
- •6,3.3.3. Азотный лазер [21]
- •6.3.3.4. Эксимерные лазеры [22]
- •6.4. Жидкостные лазеры (лазеры на красителях) [23]
- •6.4.1. Фотофизические свойства органических красителей
- •Синметные Тршетные состояния состояния
- •6,4.2, Параметры лазеров на красителях
- •Модулированной добротностью.
- •Зеркало накачки
- •6.5. Химические лазеры [26f 27]
- •6.5.1. Лазер на hf
- •6.6. Полупроводниковые лазеры [28]
- •6.6.1.3. Излучательные и безызлучательные переходы
- •6.61.4. Квазиуровни Ферми
- •6.6.2.1. Лазер на гомопереходе
- •6.6.2.2. Лазер на двойном гетеропереходе
- •6*6.4. Применения полупроводниковых лазеров
- •6.6.5. Упрощенная теория полупроводникового лазера
- •6.7. Лазеры на центрах окраски [37]
- •3EpKpj7i? с „высокой
- •I V/ ospxcuw Сатрираше rtrtacmuxxti
- •6,8. Лазер на свободных электронах [3.8]
- •6.9. Рентгеновские лазеры
- •6.10. Сводка параметров
- •Назовите хотя бы четыре лазера, длины волн которых попадают в ик-область спектра.
- •Вычислите ширину лэмбовского провала для с02-лазера с продольной прокачкой и сравните ее с доплеровской шириной.
- •Литература
- •7.1. Введение
- •7.2. Монохроматичность
- •7.3. Комплексное представление полей
- •7,4. Статистические свойства лазерного излучения и излучения тепловых источников
- •7.5. Когерентность первого порядка [3]
- •7.5.1. Степень пространственной и временной когерентности
- •7.5.2. Измерение пространственной и временной когерентностей
- •Сзетазал волна
- •7.5.3. Соотношение между временной когерентностью и монохроматичностью
- •7.5.5. Пространственная и временная когерентность одномодовых и многомодовых лазеров
- •7.6. Направленность
- •7.6.1. Пучки с полной пространственной когерентностью
- •(Лампы).
- •7.7. Лазерная спекл-картина [6, 7]
- •7.8. Яркость
- •7.9. Сравнение лазерного и теплового излучений
- •Литература
- •Преобразование лазерного пучка: распространение, усиление, преобразование частоты, сжатие импульса
- •8.1. Введение
- •8.2. Преобразование в пространстве; распространение гауссова Пучка
- •8.3. Преобразование амплитуды: лазерное усиление [6—8]
- •8.4. Преобразование частоты; генерация второй гармоники и параметрическая генерация [9-11]
- •8.4.1. Физическая картина
- •Химическая формула
- •8.4,1.2, Параметрическая генерация
- •8*4,2. Аналитическое рассмотрение
- •8.4.2.1. Параметрическая генерация
- •2Ш ф exp[/(aJte)l (8.90а)
- •8.5. Временное преобразование; сжатие импульса
- •6;Ic Дифракаматая решетка Сжатый импульс " о, г т д ифрякцаонноя решетки Одн&уюдззсе оптическое волокно
- •6 Пс примерно в 10 раз.
- •Литература
- •Полуклассическая теория взаимодействия излучения с веществом
- •Пространственно-зависимые скоростные уравнения
- •Теория активной синхронизации мод для однородно уширенной линии
- •Литература
- •Глава 1
- •Глава 2
- •Глава 3
- •Глава 4
- •Глава 5
- •Периодическая последова-
- •При замене суммы интегралом получается не тельность импульсов, а одиночный импульс.
- •Глава 6
- •Глава 7
- •Только в 2 раза. .
- •Глава 8
- •Введение
- •5.3. Непрерывный режим работы лазера 245 .
- •6. F Полупроводниковые лазеры г28м
2.9. Молекулярные системы
В этом разделе мы применим некоторые результаты и идеи предыдущих разделов к частному случаю молекулярных сред, поскольку последние играют очень важную роль в области лазеров. Ограничимся вновь описанием лишь основных свойств сложных явлений, которые при этом происходят. Однако наше
рассмотрение в действительности является основой для более глубокого понимания лазерной физики таких систем, как молекулярные газовые лазеры или лазеры на красителях. С целью более глубокого изучения данного предмета читатель может обратиться к специальной литературе [17].
2,9,1. Энергетические уровни молекул
В общем случае полная энергия молекулы представляет собой сумму следующих четырех вкладов: 1) электронной энергии Ее, обусловленной движением электронов вокруг ядер; 2) колебательной энергии Ev, связанной с движением (колеба- ниями) ядер; 3) вращательной энергии Еп обусловленной вра- щением молекулы, и 4) энергии поступательного движения. По- следнюю мы исключим из нашего рассмотрения, поскольку она, как не квантуется. Остальные же вклады в энергию
квантуются. Прежде чем перейти к подробному обсуждению, поучительно из простых соображений оценить по порядку величины разность энергий между электронным (АЕе), колебательным (Д£«) и вращательным (A£V) уровнями. Порядок величины Д£е дается выражением
ЬЕе~Н2/та\ (2.171)
где т — масса электрона, а — размер молекулы и ft = /г/2я. Действительно, неопределенность положения внешнего электрона молекулы составляет величину порядка а, неопределенность его импульса - ft/a и. следовательно минимальная кинетическая энергия равна fV/ma2. В двухатомной молекуле разность энергий между двумя колебательными уровнями А£с приближенно записывается в виде
Д£„ = /to, «[А (Ко/М)1'\ (2.172)
где М — масса атома, а Ко — упругая постоянная для притяжения двух атомов. Мы считаем, что изменение расстояния между атомами на величину, равную размеру мЬлекулы а, должно привести к изменению энергии, равному примерно ЬЕе, поскольку такое изменение расстояния между атомами вызвало бы значительное изменение электронных волновых функций. Следовательно, можно положить Ко да Д£е/а2. При этом из выражений (2.171) и (2.172) получаем
Д£„ = (т/М)фАЕе. (2.173)
Вращательная энергия по порядку величины равна ft2/(/ + + 1)/2Ма2, где / — целое положительное число (вращательное квантовое число). Таким обр азом, разность вращательных энергий Д£г между уровнями / ~ 0 и / = 1 дается выражением
^~w~(1),/2a^. (2Л74>
где мы использовали формулы (2.171) и (2Л73). Так как отношение m/Mzz Ю-4, отсюда следует, что расстояние между вращательными уровнями составляет около одной сотой расстояния между колебательными уровнями. В свою очередь разность энергий между колебательными уровнями составляет около одной сотой величины &Ее. Действительные диапазоны частот переходов, в согласии с вышеприведенными рассуждениями, оказываются для электронных (AEe/h)t колебательных (AEv/h) и вращательных (AEr/h) переходов приблизительно равными соответственно (25—50) • 103 смт"1, 500—3000 см-1 и 1—20 см-*1.
После этих предварительных рассуждений перейдем теперь к более детальному рассмотрению простейшего случая, а именно молекулы, состоящей из двух одинаковых атомов. Следуя приближению Борна — Оппенгеймера, рассмотрим вначале два атома, находящихся на расстоянии R друг от друга. Решая уравнение Шрёдингера для этого случая, можно затем найти зависимость энергетических уровней от расстояния между атомами в молекуле. Даже и не решая уравнение (которое обычно является очень сложным), нетрудно понять, что зависимость
энергии от R должна иметь вид кривой, изображенной на
рис. 2.23, где в качестве примера показаны основной уровень 1 и первое возбужденное состояние 2. Очевидно, что если расстояние между атомами очень большое (R оо), то энергетические уровни будут такими же, как и у изолированного атома. Если расстояние R между атомами конечно, то вследствие их
взаимодействия энергетические уровни будут смещаться. Поскольку производная от энергии по R представляет собой силу, с которой атомы действуют друг на друга, можно показать, что вначале на больших расстояниях эта сила является силой притяжения, а затем на малых расстояниях она становится отталкивающей. Сила равна нулю, когда расположение атомов соответствует минимуму (например, R0) каждой кривой. Следовательно, это и есть то расстояние между атомами, которое они стремятся занять (при отсутствии колебаний). Заметим, что кривая зависимости энергии от R для возбужденного состояния
сдвинута вправо относительно кривой, соответствующей основному состоянию. Это указывает на то, что среднее межатомное расстояние в возбужденной молекуле больше, чем в молекуле,
находящейся в основном состоянии.
До сих пор мы рассматривали случай, когда атомы удерживаются на определенном расстоянии R друг от друга. Предположим теперь, что атомам, располагавшимся на расстоянии R(R^Ro) друг от Друга, предоставили свободу. Тогда они начнут колебаться около равновесного положения i?o. При этом полная энергия будет равна сумме рассмотренной выше энергии и колебательной энергии. Последнюю можно вычислить, если заметить, что кривые на рис. 2.23 представляют также (с точностью до произвольного постоянного слагаемого) изменение потенциальной энергии двухатомной системы в зависимости
Рис.
2.23.
Энергетиче
ские уровни двухатом
■4
ИОН
молекулы.
от расстояния R. При малых амплитудах колебаний вблизи положения i?o кривая 1 может быть аппроксимирована параболой, которая означает, что возвращающая сила между двумя атомами является упругой, т. е. она пропорциональна смещению от положения равновесия. В этом случае задача имеет хорошо известные решения (гармонический осциллятор). Таким образом, получаем эквидистантно расположенные энергетические уровни с расстоянием между ними Av<>, определяемым выражением (2.172), в котором упругая постоянная Ко равна кривизне параболы. Следовательно, если учитываются колебания атомов относительно их положений равновесия, то, как видно из рис. 2.23, энергетические состояния (для каждого из двух электронных состояний) определяются уровнями 0, 1, 2 ... . Заметим, что уровень v — 0 не совпадает с минимумом кривой
энергии, поскольку нулевая энергия гармонического осциллятора, что хорошо известно, равна конечной величине /zvo/2. Энергия системы теперь уже не описывается кривыми 1 и 2, поскольку положения атомов не являются фиксированными. Поэтому вместо зависимостей, приведенных на рис. 2.23, иногда используют более простое представление в виде, показанном на рис. 2.24.
Однако энергетические кривые на рис. 2.23 в действительности имеют более глубокий смысл, чем на рис, 2.24. Предположим,
3 .
1
например, что молекула находится на колебательном
о'=о
«
3
• • •
2
1
I
Рис.
2.24.
Колебательные
уровни,
принадлежащие
двум
различным
электронным
состояниям.
Заметим,
что
рисунок
неверно
отражает
масштаб,
поскольку
расстояние
между
электронными
уровнями
обычно
приблизительно
в
102раз
превышает
расстояние
между
соседни-ни
колебательными
уровнями. подуровне
v"
=
3
основного уровня 1. Из рис. 2.23 нетрудно
видеть, что расстояние R
между
ядрами атомов молекулы колеблется
между
значениями, соответствующими точкам
Р и Р\
показанным
на рисунке. Наконец, следует заметить,
что при больших амплитудах колебаний
около положения равновесия /?0
изменение потенциальной энергии нельзя
аппроксимировать параболой.
Следовательно, эти более высокие ные
уровни не являются эквидистантными
. Заметим также, что для многоатомных
молекул все еще остается справедливым
представление, приведенное на рис.
2.23, при условии, что R
можно
рассматривать как некоторую координату,
которая может описывать данную
колебательную моду. Рассмотрим,
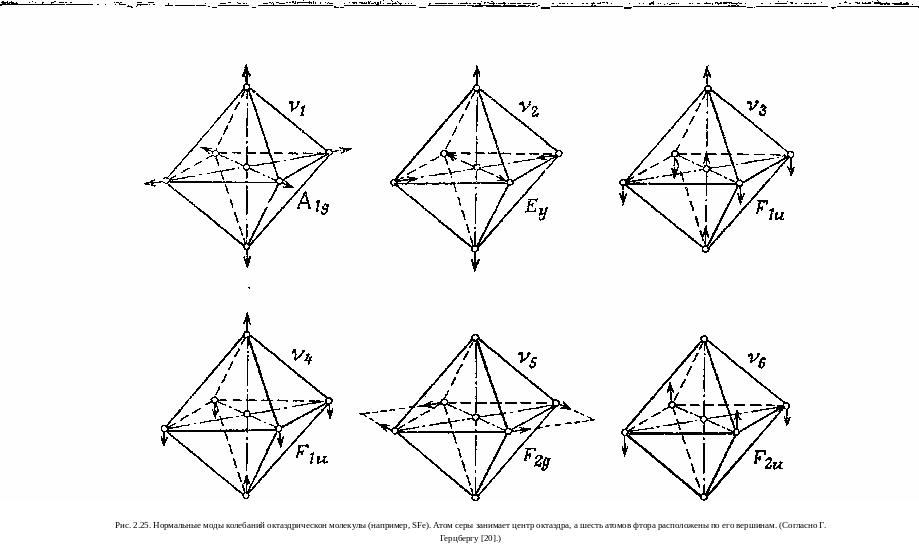
например, молекулу SF6,
имеющую октаэдрическую конфигурацию
(рис. 2.25), в которой
подуровне
v"
=
3
основного уровня 1. Из рис. 2.23 нетрудно
видеть, что расстояние R
между
ядрами атомов молекулы колеблется
между
значениями, соответствующими точкам
Р и Р\
показанным
на рисунке. Наконец, следует заметить,
что при больших амплитудах колебаний
около положения равновесия /?0
изменение потенциальной энергии нельзя
аппроксимировать параболой.
Следовательно, эти более высокие ные
уровни не являются эквидистантными
. Заметим также, что для многоатомных
молекул все еще остается справедливым
представление, приведенное на рис.
2.23, при условии, что R
можно
рассматривать как некоторую координату,
которая может описывать данную
колебательную моду. Рассмотрим,
например, молекулу SF6,
имеющую октаэдрическую конфигурацию
(рис. 2.25), в которой
атом серы располагается в центре октаэдра, а шесть атомов фтора находятся в ее углах. Если теперь выбрать симметричную колебательную моду, показанную на том же рисунке (мода A\g), то увидим, что за координату i? может быть принято расстояние между атомом серы и каждым из атомов фтора. В действительности такая молекула, как SF6 (рис, 2.25), обладает шестью независимыми, невырожденными колебательными модами. Потенциальная энергия U общего состояния молекулы
зависит от всех шести колебательных координат молекулы и поэтому должна быть представлена в семимерном пространстве. Соответственно представление на рис. 2.23 можно теперь рассматривать как часть этой с ем и мер ной функции, когда изменяется лишь одна колебательная координата'.
Т
i
l
Ч
3
2
щ
*
J=
О
j
гт
—j—t
,—
j
г
I
i
i
I
I (ill
I
I
I i i I
l
I
/?-
вет$ь
i i
!
!
Mil
ii |
|
Р
-
,fr<OT6
в виде
4 • 3 •
= I), (2.175)
■4>
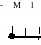
где вращательная постоянная В = /?2/8л2/, причем / — момент инерции молекулы относительно
J"-О
Рис. 2.26. Вращательные уровни. принадлежащие двум соседним колебательным состояниям молекулы. Стрелками указаны переходы, соответствующие Р- и
/?-ветви.
оси, перпендикулярной линии, соединяющей ядра, и проходящей через центр масс. Таким обр азом,
общая энергия системы Представляет собой сумму электронной, колебательной и вращательной энергий. Соответственно
энергетические подуровни, ска-
жем, колебательных уровней V = О и v' = 1 основного состояния, будут выглядеть так, как показано на рис. 2.26. Заметим, что в отличие от (приблизи- тельно) эквидистантно расположенных колебательных уровней расстояние между последовательными вращательными уровня- ми не а увеличивается линейно с ростом враща- тельного квантового числа /, т. е. Er(J)—Er(J—1)= 2BJ.
