2.6. Насыщение

Целью настоящего раздела является изучение поведения двухуровневой системы (с частотой перехода vo) в среде в при_ сутствии сильной монохроматической электромагнитной волны с интенсивностью / и частотой v « vo. В общем случае падаю­щая волна будет стремиться уравнять населенности Ni и N₂ обоих уровней. Действительно, если первоначально населен_ ность N\ больше населенности N₂, то процесс поглощения (WNi) будет преобладать над процессом вынужденного излуче­ния (why, иными словами, большее число атомов совершает переход 1^2, а не 2-М. Таким образом, при достаточно вы­сокой интенсивности / населенности обоих уровней будут стре_

миться к выравниванию. Это явление называется насыщением.

2.6.1. Насыщение поглощения; однородно уширенная линия

Рассмотрим вначале поглощающий переход (W,. > N2) и

_{предположим, что линия при этом переходе является однородно}

уШиренной. Учитывая как спонтанное, так и вызванное падаю_ щей волной вынужденное излучение (рис. 2.14), для населенно_

стей N\ и ЛГ₂ двух уровней можно написать следующие два уравнения:

JV, + ЛГ₂ = N_t, (2.131а)

£^^^j^f^= (Л^2 ^^i) N2/^* (2.1316)

В уравнении (2.131 а) через ДО* обозначена полная населенность

уровней в данной среде. Если

AN = N_X-N_2i (2.132)

то оба уравнения (2.131) можно привести к одному дифферен_ циальному уравнению:

ДАТ _в + 2W)+Nt/x. (2 Л 33)

В стационарном случае, когда АЙ =0, получаем

AN = N_t/(l + 2W%). (2 Л 34)

Следовательно, разность населенностей AN между двумя уров- нями зависит от т и W, т. е. от времени релаксации верхнего уровня (которое является ^ „

параметром среды) и от ин- ² д | I ²

тенсивности / падающего ' ,11

излучения. С увеличением / Л Л Л wu им, uJ_T

вероятность вынужденных и^|0ф^г- ^ ^ *'/^г

переходов также увели- 1 I чивается, а это приводит к М, I ^ Т е,

уменьшению разности насе- Рис. 2.14. Двухуровневая система, вза-ленностей AN_f И В случае имодействующая с электромагнитной Wx> ^{1 мы} имеем ДДГ ж 0, волной, имеющей интенсивность /.

т. е. Ni ж N2 « Nt/2. Та­ким образом, населенности двух уровней стремятся стать оди_

наковыми.

Для того чтобы в среде поддерживать данную разность на_ селенностей ДЛГ, в единичном объеме среды должна поглощать­ся определенная мощность (dP/dV) падающего излучения. Эта мощность дается выражением

dP/dV = (Av) WAN = (hvWtWfc + 2Гт), (2.1 35)

которое в случае насыщения (при Wx^ 1) принимает вид

(dP/dV)^ (Ay) N_t/2x. (2.136)

Отсюда следует, что мощность (dP/dV) _s> которая должна по_ глощаться системой, чтобы последняя находилась в состоянии насыщения, равна (как и ожидалось) мощности, теряемой сре­дой вследствие релаксации верхнего уровня.

Иногда полезно иметь выражения (2.134) и (2.135) перепи­санными в более удобном виде, Для этого прежде всего заме­тим, что, согласно (2,62), W можно выразить следующим об­разом:

B7 = (7//Av; (2.137)

здесь 0 — сечение поглощения рассматриваемого перехода. По­лученное соотношение позволяет переписать выражения (2.134) и (2,135) следующим образом:

AN _

dP/dV (dPfdVh

1

1 + Wis) ' ///

⁼ _{1 +<///,)}

(2.1 38) (2.1 39)

где

^l_s ^{= hv/2ax}

(2.1 40)

представляет собой параметр, который зависит от свойств дан­ной среды и частоты падающего излучения. Физический смысл

Насыщающий пучок [Куц

этого параметра очевиден из выражения (2.138V Действительно, при / = /* полу­чаем AiV = Nt/2. Когда v ~ vo, величина I_s зависит лишь от параметров перехода. Эта величина называется интенсив-

^{ностью насыщения.}

Покажем теперь, как меняется фор- * п*х ъх ма линии поглощения с увеличением ин-

Рис. 2.15. Измерение ко- _Т.

эАФиииентов поглоше- тенсивности / падающего монохромати-нГТусиления на ча- ческого излучения. С этой целью рас-стоте V' [/(v) > /' (V)]. смотрим идеализированный эксперимент,

схема которого изображена на рис. 2.15. В таком эксперименте поглощение измеряется с помощью проб­ного сигнала переменной частоты v', интенсивность /' которого достаточно мала, так что этот сигнал не вызывает в системе за­метного возмущения. В реальной ситуации необходимо быть

^{уверенным в том, чтобы пробный сигнал взаимодействовал}

только с областью насыщения, а для этого он должен распро­страняться в виде более или менее коллинеарных пучков. При выполнении этих условий коэффициент поглощения, измеряе­мый с помощью пробного пучка, дается формулой (2.87), где gt (Av) = g (v^f— vo), а разность населенностей N\ — N2= AiV определяется выражением (2.138), Следовательно, можно напи­сать следующее выражение:

а— )+ (_f/f_s) • (2.141)

где ао — ао (v' —vo) — коэффициент поглощения в случае,

когда насыщающая волна на частоте v отсутствует (т. е. / = 0), причем

^ = jS^M^^N^'-^). (2-142)

ПО-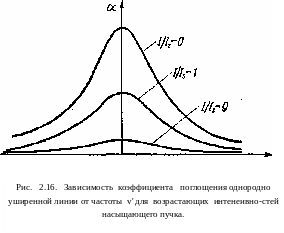

Из выражений (2.141) и (2.142) следует, что с увеличением ин­тенсивности / насыщенного пучка коэффициент поглощения па­дает. Однако форма линии остается прежней, поскольку она в любом случае описывается функцией g(v'-vo). На рис, 2.16 представлены три кривые, показывающие зависи_ мреть коэффициента глощения а от частоты v для трех различных зна­чений I/Is.

В заключение этого раздела рассмотрим слу_ чай, когда насыщающая

электромагнитная волна состоит не из непрерыв_

ного пучка, а из импульса света интенсивностью / — = /(/). Чтобы составить себе физическое пред­ставление о том, что про_

исходит в этом случае, ограничимся сравнением двух предельных ситуаций, когда длительность импульса либо очень велика, либо очень мала по сравнению с временем жизни т верхнего уровня.

Если постоянная времени изменения интенсивности света в импульсе очень мала но сравнению с т, то благодаря насыще­нию разность населенностей AN будет также очень медленно меняться со временем. Поэтому в (2.133) можно предположить, что

_{|ДЛП<ЛГ,/т}

^(2.142а)

Соответственно AN по-прежнему определяется стационарным уравнением (2.134) или, что эквивалентно, уравнением (2.138), где теперь I=I(t). Механизм насыщения в этом случае такой же, как и для непрерывного пучка. Теперь нетрудно найти ус­ловие, при котором удовлетворяется неравенство (2.142а). Если предположить для простоты, что /<C/s (слабое насыщение), то из уравнения (2.138) получим AN(t) т N_t{\ — [I(t)//_s]}.Под­ставляя это выражение в (2.142а), имеем

dI/dt\<IJx. (2.1426)

Если же длительность светового импульса очень мала по сравне_ нию с временем жизни т, то можно считать, что в (2,133) член 2WAN, соответствующий вынужденному излучению, преобладает над членом (Nt —ДЛ)/т, соответствующим спонтанному излу_

чению, т. е.

^(N_t ^{- AN)/x < 2WAM. (2Л42в)}

В этом случае (2.133) принимает вид

_{ДАТ (0 = _ 2WAM = - (2oJhv) / (О AN, (2.142г)}

где было использовано также равенство (2.137). Интегрирова­ние последнего выражения с начальным условием АЛ-(-оо) = = Nt дает

^{(*) = N}_t ^{ехр Г - (2o/hv) J / (О J/J. (2.142д)}

Это выражение можно преобразовать к более доступной фор­ме, если определить плотность энергии облучения Г(/) как

_t

^{T(f)= [ l{t)dt (2.142е)}

— оо

^{и плотность энергии насыщения среды Y$ как}

T_s^hv/2a. (2.142ж)

Тогда из равенства (2.142д) находим

^{д# (О = iV^exp - [Г (/)/rj. (2.142з)}

Мы видим, что в этом случае параметры насыщения определя_ ются плотностью энергии облучения, а не его интенсивностью. В соответствии с (2Л42з) разность населенностей, образующая­ся в среде после прохождения импульса, дается выражением

ДЛ^ос = M_texp _ [1\/Г₅], (2.142и)

где Tt — полная плотность энергии облучения светового им_ пульса. Таким образом, плотность энергии насыщения среды может рассматриваться как плотность энергии, которой должен обладать импульс, чтобы создать разность населенностей ДМ» = Nt/e. Условие, при котором выполняется неравенство (2.142В), можно теперь представить в аналитическом виде. Под­ставляя[ (2.142з) в (2.142b), находим

1 - ехр [- (Г/Г,)] _< ^_ехр [_ (Г/Г,)]; (2.142к)

здесь мы также использовали выражение (2.137). Нел и для про­стоты вновь рассмотреть случай слабого насыщения, т. е. Г<С <Г₅, то из (2.142к) с помощью (2.142ж) получаем

Г (t) = Idt «С т/(0>

(2.142л)

оо

что на самом деле доказывает справедливость при

ловии, что длительность импульса много меньше т.

Вычислив разность населенностей, образующуюся благодаря насыщению при облучении световым импульсом, с помощью вы­ражения (2.86) можно получить соответствующий коэффициент поглощения среды для однородно уширенной линии. Для свето­вого импульса, который является соответственно медленным или быстрым по сравнению с значение а дается выраже­нием (2.141) [причем/ = /(/)] или

а=ctg'exp'I—^I\(£)/r_s],

(2 Л 42м)

где ао — коэффициент ненасыщенного поглощения.

Заметим, что в импульсном режиме так лее, как и в случае непрерывного режима, форма линии поглощения при насыщении не меняется.

2.6.2. Насыщение усиления; однородно уширенная линия

Рассмотрим случай, когда переход 2-^1 усиливает излуче­ние, а не поглощает его. Предположим, что среда ведет себя как четырехуровневая система (рис. 2.17) и что инверсия населен-ностей между уровнями 2 и 1 создается благодаря некоторому процессу накачки. В дальнейшем будем считать, что пере­ходы 3->-2 и 1 -*g осуществляются со столь большой скоростью, что можно по­ложить N$ ж N\ ж 0. При таких упро­щающих предположениях можно запи­сать следующее скоростное уравнение для населенности уровня 2:

^{cLN%ldt "==— (Л/f - ~ tt^A^2- -Л^з/т,}

(2 Л 43)

где W_a— скорость накачки, a Nt — суммарная населенность.

В равновесном состоянии (т. е. когда dN₂jdi = 0) из уравне­ния (2.143) находим

#₂ = W_pN_tx/(l + Wx). (2.144)

При выводе этого выражения мы предположили, что W_pt< 1; это условие, как правило, выполняется в лазерных материалах, С помощью (2.137) выражение (2.144) можно переписать в виде

где N20— WpNtx —населенность уровня 2 в отсутствие насы­щающего пучка (т. е. при / — 0), а

I_s = hv/ax. (2.146)

Сравнивая (2.146) и (2.140), мы находим, что при тех же самых значениях величии Av, а и т интенсивность насыщения I_s в че­тырехуровневой системе в два раза больше, чем в двухуровне­вой системе, показанной на рис. 2.14.

В эксперименте, схематически изображенном на рис. 2.15, пробный пучок на частоте V позволяет теперь измерять усиле­ние, а не поглощение. В соответствии с выражениями (2.88), (2.88а) и (2.145) результирующий коэффициент усиления мож­но записать следующим образом:

_<^2Л47)

где g₀ = oN₂o — коэффициент усиления, когда насыщающий пу­чок отсутствует (коэффициент ненасыщенного усиления). Вели­чину go можно найти с помощью выражения (2.83):

go^ir^-irlliPv'NiQgiv' — v₀). (2.148)

Из (2.147) и (2.148) следует, что, как и в случае поглощения,

рассмотренного в предыдущем разделе, коэффициент усиления

g уменьшается с увеличением интенсивности /, но форма линии

при этом остается неизменной.

В заключение этого раздела так же, как и в конце преды­дущего, рассмотрим случай, когда насыщающая электромагнит­ная волна представляет собой световой импульс интенсив­ностью /(/)• Если постоянная времени изменения интенсивности светового импульса достаточно мала по сравнению с временем жизни т, то по-прежнему в (2.143) можно пренебречь временной производной величины N₂ по сравнению с другими членами. Таким образом мы получаем снова выражение (2.145) для на­селенности верхнего уровня и выражение (2.147) для коэффи­циента усиления, причем интенсивность / теперь является функ­цией I(t)_f а интенсивность насыщения l_s определяется выраже­нием (2.146). Если длительность светового импульса много меньше времени жизни т, то величиной W_p(Nt -- .Vo), о преде­ляющей накачку, и величиной N₂/r, определяющей спонтанную релаксацию, можно пренебречь по сравнению с членом WN₂, связанным с вынужденным излучением. Таким образом, мы по_ лучаем

dNJdt = - (aI/hv)N₂; (2.148а)

здесь мы еще раз использовали (2.137), Интегрирование по_ следнего уравнения дает следующее выражение:

N₂(t) = N₂₀exp { - [Г (0/Г,]>, (2.1486)

где N₂ = W„Na- населенность уровня 2 до начала воздействия импульса, Г(/) — плотность энергии облучения [см. (2.142е)],а

T_$ = hv/o (2.148в)

— плотность энергии насыщения усилителя. Сравнивая (2.148в) и (2.142ж), мы видим, что плотность энергии насыщения усили­теля, работающего по четырехуровневой схеме, вдвое больше аналогичной величины для поглотителя. При этом насыщенный коэффициент усиления дается выражением

g = g₀exp{-ir<0/r,]>. (2.148г)

_{где go = 0N30 - ненасыщенный коэффициент усиления.}

Заметим раз, что в случае режима так же,

как и в случае непрерывного режима, форма линии поглощения при насыщении не меняется.