2.4, Спонтанное излучение

Целью настоящего раздела является вычисление вероят­ности спонтанного излучения .4, определяемой выражением (1.2). К сожалению, полуклассическое рассмотрение взаимо­действия излучения с веществом не позволяет, как будет пока­зано ниже, адекватно предсказать и понять явление спонтанно­го излучения. Тем не менее для начала полезно рассмотреть это явление с позиций полуклассического подхода. Полученные результаты затем будут сопоставлены с результатами точного квантовоэлектродинамического анализа, в котором квантуют­ся как атом, так и излучение.

2.4 Л. Полуклассический подход

Прежде всего рассмотрим с чисто классической точки зре­ния электрический диполь, колеблющийся с частотой <о₀. Если считать положительный заряд неподвижным, то в системе коор­динат положительного заряда мгновенное положение т отрица­тельного заряда можно записать в виде

_г

—

^r₀ ^{cos(ю^ + ф) = Re [r^exp (т}₀^()\,

(2.89)

где Re обозначает действительную часть, а т'₀ =г₀ехр(г'^).

Из уравнений Максвелла следует, что движущийся с ускорением электрический заряд излучает электромагнитную волну, мощ­ность которой пропорциональна квадрату ускорения. Таким образом, можно показать [4], что колеблющийся электрон из­лучает в окружающее пространство мощность которая дает­ся выражением

_{Р. =}

2 4 12Я8₀С|) *

(2.90)

- амплитудное значение электрического ди-п — показатель преломления среды, a со —

где [л=ег₀ = е}\ г₀ '

^{польного момента,}

скорость света в вакууме. Среднее значение полной энергии ко­леблющегося электрона определяется суммой средних значений кинетической и потенциальной энергий. Поскольку, как извест­но, эти значения равны друг другу, <£> = (Кинетическая энер­гия) + (Потенциальная энергия) = 2<Кинетическая энергия).

Следовательно,

(Е) = 2 (т/2) (у²) = (1/2) т (ц©о/е)²;

(2.91)

здесь т — масса электрона, а <у²> — средний квадрат скорости. За время dt осциллятор будет терять энергию, равную dE = -P_rdt. Таким образом, используя выражения (2,90) и (2.91), можно написать

(2.92)

dE = — -&-dt,

Ткл

где

3

2 »

КЛ

(2.93)

Вследствие дипольного излучения амплитуда го колебаний, а следовательно» и р будут со временем уменьшаться. Однако, по­скольку величина т_кл не зависит от р, она будет оставаться по­стоянной. В этом случае из уравнения (2.92) следует, что энергия £ будет экспоненциально уменьшаться с постоянной времени т_кл. Поэтому с классической точки зрения эта величина называется временем жизни колеблющегося диполя.

Вернемся теперь к рассматриваемой нами задаче двухуров­невой атомной системы При спонтанном излучении атом испы­тывает переход 2 1, и для описания волновой функции атома можно снова применить выражение (2.29). Следовательно, при­обретаемый атомом дипольный момент М описывается псе тем же выражением (2.32). В действительности для состояний опре­деленной четности первые два члена в выражении (2.32) равны нулю, поскольку как I щ 1² так и I а» 1² — четные функции коор­динаты г. В любом случае эти два члена не зависят от времени.

Если для простоты рассмотреть состояния с определенной чет­ностью, то выражение (2.32) упрощается, и мы приходим к выражению (2.33), т. е.

М = Re { [ехр (ш^а^Ц }. (2.94)

По аналогии е рассмотренным выше случаем классического осциллятора мы ожидаем, что именно этот осциллирующий с частотой v₀ = ioo/2jt член ответствен за излучение энергии в окружающее пространство и, следовательно, описывает процесс спонтанного излучения. При этом с помощью простого условия сохранения энергии можно вычислить скорость изменения ве­личины |а₂|²в единицу времени, т. е.

hv₀= _ p_fy (2.95)

где мощность излучения Р_г можно найти из соотношения (2.90), если учесть, что в соответствии с (2.94) (-1 = 2 l^a*^ |- Тогда

уравнение (2.95) можно переписать в виде

^d|a_{*'* = L_iщ \}²_\а2\² _{= — (1 - I a, р)|а,|}²_{, (2.96)}

dt Тспонт депонт

где мы использовали соотношение (2.30) и определили харак­терное время Тспонт как

16л;^п|ц|² *

спонт

(2.97)

которое называется спонтанным временем

жизни уровня 2. Решение уравнения (2.96) имеет вид

_{l*r-H'-*b(i=S)]'} ⁽²_'⁹⁸⁾

где io определяется начальными условиями, т. е. значением | а₂ (0) |². Действительно, из (2,98) видно, что

^{IO2(0)P-(l/2)fl-th}

_(2,99)

откуда для данного значения |а₂(0) |² (при условии, что оно меньше единицы) однозначно вычисляется *₀. В качестве при­мера на рис. 2.11 показана временная зависимость величины 102(01² при начальном условии \а₂(0) |² = 0,96. Заметьте, что

а?

ния

и

от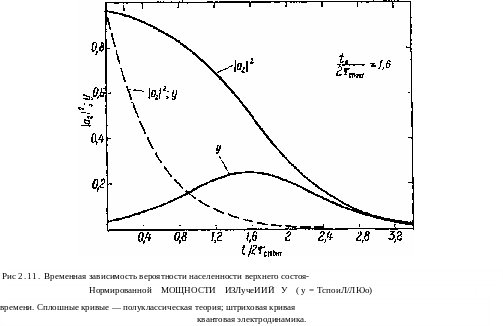

выбор различных значений |#2(0)|² просто изменяет значение U в выражении (2.98), т. е. сдвигает начало временной оси. На этом же рисунке приведено также изменение со временем нор­мированной мощности излучения Р_г. Для дальнейшего рассмот­рения существенно, что временное поведение \u₂(t)

_можно

аппроксимировать экспоненциальной зависимостью вида

I <h (ОР = 1а₂(0)Рехр [—(*/т_спонт)] (2.100)

только тогда, когда |Д2(0)J² < 1. В этом случае действительно в (2.96) можно положить \й\\² 1 и сразу получить выраже­ние (2.100).

Наиболее важным является случай, когда |я₂(0)|²=1. При этом из (2.99) мы находим, что to = оо, т. е. в соответ­ствии с полуклассической теорией атом релаксировать не должен. Действительно, если |a₂(0) ² = 1, то |fli(0) I² = 0 и из (2.96) следует, что d\a,\ydt=6. Можно взглянуть на этот случай с другой стороны, обратив внимание на то, что момент М в выражении (2.91) исчезает при й\ (0) = 0. Поскольку теперь атом не имеет осциллирующего дипольного момента, он не мо­жет излучать и поэтому пребывает в состоянии равновесия. Вы­ясним, насколько устойчивым является это состояние равновесия. Для этого представим себе, что атом возмущен, т. е. |ai| #0 при t - 0. Физически это означает, что благодаря такому воз­мущению существует конечная вероятность | а\ [² обнаружить атом на уровне 1. Теперь из уравнения (2.94) видно, что возни­кает дипольный момент, осциллирующий на частоте <в₀. Этот дипольный момент будет излучать энергию в окружающее про­странство, и атом начнет релаксировать на уровень 1. Это при­водит к уменьшению |а₂|², и атом отодвигается все дальше от положения равновесия. Таким образом, рассматриваемое со­стояние атома является неустойчивым.

Прежде чем продолжить рассмотрение, подытожим основ­ные результаты, полученные в рамках полуклассического под­хода: 1) в общем случае временное поведение вероятности |а₂ ² можно описать через гиперболический тангенс [см. (2.98)], но эта зависимость в случае очень слабого возмущения, т. е. когда | а₂(0) |² <С 1» может быть аппроксимирована эксио-нентой [уравнение (2.100)]; 2) если атом первоначально нахо­дится на верхнем уровне [т. е. |а₂(0)|²=1], то имеет место

^{состояние неустойчивого равновесия и никакого излучения не}

^{происходит,}