6;Ic Дифракаматая решетка Сжатый импульс " о, г т д ифрякцаонноя решетки Одн&уюдззсе оптическое волокно

Рис. 8.12. Экспериментальная установка для сжатия импульсов.

^{В соответствии с (8.105) эта величина дается выражением}

dx_A = L (d^/dm²) rfco. (8 Л 06)

Представив величину dx* в форме (8.106), обычно определяют дисперсию групповой скорости (ДГС) в виде

JXYC = d²kjd®\ (8.107)

Заметим, что поскольку и_g = dw/dk, можно также написать

g

v

d

ДГС =

s

1 dv

rtco

(8.108)

^{Из соотношений (8.106)-(8.108) следует, что дисперсию}

менной задержки можно представить в виде

^вре-

dx_d ^ d²k d (Lfv_g)

day d®² rfo

(8.109)

Сделав эти предварительные замечания, можно продолжить рассмотрение метода сжатия сверхкоротких лазерных импуль­сов. Соответствующее устройство схематически представлено на рис. 8.12. Импульс лазера, работающего в режиме синхрониза­ции мод, с относительно небольшой максимальной мощностью (например, Р_р = 2 кВт) и большой длительностью импульса (на­пример, %_р = 6 пс) пропускается через одномодовое кварцевое оптическое волокно подходящей длины (например, L = 3 м). Длина волны импульса (например, К = 590 нм) попадает в об­ласть положительной дисперсии групповой скорости волокна

(обычно Ж 1,3 мкм). Заметим, чго, согласно (8.108), поло- жительная дисперсия групповой скорости означает» что груп- повая скорость уменьшается с увеличением несущей частоты. После выхода из волокна импульс коллимируется и про- ходит через систему двух дифракционных решеток, расположенных параллельно друг другу. Наклон этих решеток и расстояние между ними необходимо подобрать вполне опреде- ленным образом, описанным ниже. При выполнении этих опре- деленных условий выходной пучок состоит из светового им- пульса, длительность которого значительно меньше, чем у вход- ного импульса (например, т« = 200 фс), и, следовательно, пико- вая мощность намного больше (например, Р_р = 20 кВт). Таким образом, устройство, изображенное на рис. 8.12, позволяет полу- чить очень большой коэффициент сжатия (например, в нашем случае около 30). Перейдем теперь к рассмотрению достаточно непростых явлений, происходящих во время сжатия импульса

Рассмотрим сначала процессы, которые имеют место при распространении импульса в оптическом волокне. Прежде всего заметим, что при данном диаметре небольшого ядра одномодо-вого волокна (~ 4 мкм) импульс создает внутри ядра очень вы­сокую интенсивность излучения. В этих условиях поле световой волны вызывает значительные изменения показателя преломле­ния б/г материала волокна. В действительности это изменение б/г пропорционально квадрату амплитуды поля импульса, так что мы можем записать б/г = /г₂/И², где для кварца п*_Е ~ « Ю-²² м²/В². Это явление обычно называют оптическим эф­фектом Керра. Поскольку интенсивность / пропорциональна А², величину б« можно записать в более общепринятом виде:

Ьп = П2,1 (/), (8.110)

где для плавленого кварца n₂i ~ 10^-'⁶ см²/Вт. Заметим, что, по-

^{здесь речь идет о световом импульсе, мы явно указали}

в (8.110) на то, что интенсивность / является функцией времени. Это что показатель преломления среды п = п₀ + 8«

(где По—показатель преломления в отсутствие поля) является также функцией времени. Если потери в волокне малы, то им­пульс может сохранить высокую интенсивность на протяжении

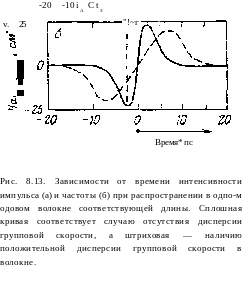
всего волокна, а это вызовет очень большую фазовую модуля­цию несущей. Предположим, что в действительности импульс на входе в волокно имеет колоколообразную форму, как показано сплошной линией на рис. 8.13, а, и пусть этот импульс распро­

страняется по бездисперсионному волокну на расстояние г. В от­сутствие дисперсии групповой скорости форма импульса не бу­дет изменяться, и импульс, пройдя расстояние г по волокну, ис­пытает сдвиг фазы ф, определяемый выражением

(О

_{kz — шлГ —} ⁽⁰_°^п_°^г _{— ®° ^}^пг

С₀ с₀

(8ЛП)

где coo — частота несущей входного импульса, а с_(} — скорость света в вакууме. Тогда мгновенно^ значение частоты светового импульса в точке с координа-

0,5

(8.112)

той можно записать в виде дЩ — kz)

dt

(й₀ 01

₇₇ ^гп_{* 'дТ}

₃

₁

_о

"111/ а 1	Г ! 1 1 ]
' У '	1 \тр\ 1 \ \ ! NX

₂₀

Таким образом, мгновенное значение частоты несущей <о'= = ©^/(0 линейно зависит от

производной мгновенной интен­сивности света по времени,

^{взятой с обратным знаком.}

Следовательно, у импульса, по­казанного на рис. 8.13, а, несу­щая частота будет изменяться со временем так, как показано сплошной линией на рис. 8ЛЗ,б. Заметим, что вблизи пика им­пульса, т. е. в той области, где временную зависимость можно описать параболой, мгновенное значение частоты несущей ли­нейно растет со временем (т. е. говорят, что импульс обладает

положительным смещением ¹⁾\ см. разд. 5.4.5). Заметим также, что смещение частоты отрицательно на крыльях импульса, т. е. при t < t_A или t > t_B на рис. 8ЛЗ,б. Явление, которое мы только что описали, носит название фазовой самомодуляции светового импульса.

Рассмотренная до сих пор физическая ситуация не дает полного представления о том, что происходит на самом деле

^п Иногда говорят также «положительный «шрп» (калька с английского positive chirp). Мы пе пользуемся этим термином так же, как и «свиппрова-нием частоты» (frequency sweep), заменяя их словом «смешение», имеющим ясный физический смысл - Прим. ред.

в волокне, поскольку мы пренебрегли положительной дисперсией групповой скорости. Этот эффект эвристически можно описать следующим образом. Рассмотрим сначала форму невозмущен­ного светового импульса в данный момент времени как функ­цию координаты z- Поскольку интенсивность импульса зависит от 2 — Vgt> где v_g — групповая скорость, зависимость интенсив­ности импульса от переменной г та же, что и на рис. 8.13 при условии, что мы изменим положительное направление оси на противоположное и умножим масштаб времени на v_g. Это озна­чает, что точка, скажем А на рис. 8.13, а, в действительности находится на переднем фронте, в то время как точка, скажем В, — на заднем фронте. Заметим теперь, что в соответствии с рис. 8.13,6 несущая частота импульса о' вблизи точки А будет ниже, чем в точке С, где частота примерно равна щ. В то же время несущая частота импульса вблизи точки В будет выше, чем в С. Поскольку мы считаем, что волокно обладает положи­тельной дисперсией групповой скорости, часть импульса вблизи

точки А будет двигаться быстрее, чем часть импульса вблизи точки С, а последняя в свою очередь будет двигаться быстрее области вблизи точки В. Отсюда следует, что при распростра­нении по волокну центральная часть импульса будет растяги­ваться. При помощи тех же соображений можно показать, что фронты импульса будут не растягиваться, а обостряться, так как в этих областях смещение частоты отрицательно. Поэтому ис­тинная форма импульса как функция времени в данной точке z будет такой, как показано на рис. 8.13, а штриховой кривой. Со­ответствующая зависимость смещения частоты показана штри­ховой кривой на рис. 8.13, б. Из рис. 8.13, а мы видим, что из-за

уширения, обусловленного дисперсией групповой скорости, пико­вая интенсивность импульса, указанного штриховой кривой, меньше, чем для сплошной кривой. Заметим также, что по­скольку параболическая часть импульса распространяется те­перь на более широкую область вблизи пика, положительное линейное смещение частоты распространяется на большую часть импульса. Установив эти общие особенности взаимодей­ствия процессов фазовой самомодуляции и дисперсии групповой скорости, мы можем показать, что если длина волокна доста­точно большая, то на выходе волокна, показанного на рис. 8.12, форма импульса и смещение частоты будут изменяться во вре­мени так, как изображено на рис. 8.14, а и б. Заметим, в част­ности, что положительное смещение частоты теперь линейно во времени на протяжении большей части импульса. Соответствую­щий спектр мощности этого импульса приведен на рис. 8.14, в. Заметим, что благодаря фазовой самомодуляции ширина спек­тра (~ 50 см-¹) заметно превышает первоначальную ширину

спектра импульса на входе в волокно (которая определялась об­ратной длительностью импульса, т. е. Av ж 0,5/tp 2,8 см-¹ для рассмотренного случая % ж 6 пс) ⁴. Отсюда следует, что ши­рина полосы на выходе в основном определяется фазовой моду­ляцией, а не длительностью его огибающей.

Предположим теперь, что импульс на рис. 8.14, а (и 8,14, б) пропускается через среду с отрицательной дисперсией группо­вой скорости. Используя те же рассуждения, что и в связи с

С В

a

_I

^{3 £ ozY}

-2D 40 О Ю 20 -SJ -25 0 ZS . 50

Время, nc •% Частота, см

Z5\ . i , i ,—г—cn—i P;

_{% 1}

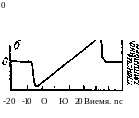^{& 0.1}

_{-да -sos}

Время, пс

Рис. 8.14. Расчетные значения самоуширения (а) и фазовой самомодуляции (б) исходного импульса длительностью 6 пс после распространения в одно­модовом волокне с положительной дисперсией групповой скорости на рас­стояние 30 м; спектр выходного импульса (в); сжатый импульс после про­хождения оптической системы с отрицательной линейной дисперсией группо­вой скорости (г). (Согласно Гришовски и Баланту

рис. 8.13, можно показать, что область импульса вблизи точки Л будет двигаться медленнее, чем вблизи точки С, а эта в свою очередь будет двигаться медленнее области вблизи точки В. От­сюда следует, что импульс будет сжиматься. Предположим те­перь, что дисперсия групповой скорости среды помимо того, что она отрицательна, не зависит также от частоты. Следовательно, дисперсия временной задержки dTd/dw будет также отрицатель­ной и не будет зависеть от частоты, т. е. %а линейно уменьшает­ся с частотой. Поскольку смещение частоты импульса увеличи­вается линейно со временем (см. рис. 8.14,6), все точки им­пульса на рис. 8.14, а в случае, когда среда имеет соответствую­щую длину, сожмутся вместе в одно и то же время. Эту длину можно определить с помощью соотношения [см. (8.103)]

(8.1 13) где 'со — полное смещение частоты импульса (~ 50 см^-1 в при­мере, приведенном на рис. 8.14, б), ат_р — длительность импульса

(~ 23 пс в примере на рис. 8.14, а). Заметим, что сжатие вме­сте всех точек импульса означает переход частотной модуляции импульса (показана на рис. 8.14) в амплитудную модуляцию. Поскольку в процессе этой операции спектр импульса сохра­няется (т. е. он по-прежнему такой же, как на рис. 8.14, в), дли­тельность сжатого импульса %"_ должна быть приблизительно

равна обратной ширине полосы спектра, т. е. т£ 2я/Дш

~ 0,75 пс. Так как первоначальная длительность импульса была равна т_а- ~ б пс (рис. 8.12, а), данный результат означает, что было достигнуто существенное сжатие импульса ^]).

Следует заметить, что приведенное выше эвристическое рас­смотрение основывалось на допущении, что импульс с частот­ным смещением может быть разделен на отдельные временные отрезки с различными частотами несущей. Хотя данная идея в принципе верна и позволяет дать простое описание явлений, бо­лее подробное рассмотрение этого подхода привело бы к некото­рым концептуальным трудностям. Однако корректное аналити­ческое рассмотрение в данном случае оказывается достаточно прямолинейным, хотя при этом физика процесса становится бо­лее сложной и далекой от интуитивного представления. Для по* лучения сжатого импульса достаточно вычислить фурье-образы £(©) импульсов, изображенных на рис. 8Л4, а и б, и умножить их в частотной области на пропускание t(®) среды с отрица­тельной дисперсией групповой скорости. При этом результирую­щий импульс получают вычислением обратного фурьс-преобра-зования произведения £(<d)f(a>). Заметим, что в среде без по­терь пропускание /(.со) представляет собой чисто фазовый член,

определяемый выражением

/(ш)=ехр(— ВД, (8.114)

где L — длина среды, а величина k = определяется диспер- сионным уравнением среды. Если среда имеет постоянную дис- персию групповой скорости, то можно разложить в ряд

Тейлора относительно частоты несущей с точ-

ностью до квадратичного члена:

¹¹ Аналогичные методы получения укороченных импульсов путем созда­ния вначале линейного частотного смешения (чирпа) с последующим сжатием импульса активно использовались в области радиолокации после Второй м и -ровой воины (радары с частотной модуляцией).

k((u) = Цщ) + к'(щ)(® — со₀) + 6" (о>₀) (со - а>₀)²/2, » (8.1 15)

где в соответствии с (8.103) и (8.107) мы имеем k'(щ) = I/ и ^(©о) =ДГС. Подставляя данное разложение в выражение (8.107) и производя обратное фурье-преобразование произведе­ния ЕШЫ>

^{находим, что если вторая производная ft,Awo)}