2Ш ф exp[/(aJte)l (8.90а)

ными. Из (8.90)

получаем соотношение Мэнли

Роу

^{(8 «9 2)}

Отсюда следует, что в рассматриваемом случае возможно 100*%-ное преобразование мощности основной волны в мощность излу­чения на второй гармонике.

В качестве первого примера рассмотрим решение системы уравнений (8.90) в случае, когда фазовое рассогласование столь велико (т. е. 1вгД& 3> 1), что во вторую гармонику преобразуем­ся лишь очень небольшая доля мощ­ности основной волны. Поэтому в правой части уравнения (8.90а) сле­дует положить Е^г (г) = Е' (0). Полу­чающееся при этом уравнение не­трудно проинтегрировать [с гранич­ным условием Е'_2ф (0) = 0]. Таким

образом, решение уравнения

_{запишется в виде}

^Е_ш ^{(0) Г ехр (- 1Ш) - 1}

_вг

(8.93)

^{откуда получаем}

sin² (AW/2) (А*'вг/2)²

Хенсивности^аРТзлучения^2<°-на основной частоте /о» от длины кристалла I при идеальном фазовом синхронизме (сялош-ные кривые) и некотором фа­зовом рассогласовании (штри­ховые кривые).

(8.94)

^2(й\2 пропор-

_(Р)

Поскольку величина

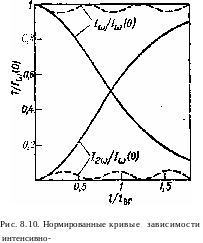
циональна интенсивнЬсти /₂, вто­рой гармоники, из последнего выра­жения нетрудно получить зависи­мость этой интенсивности от длины кристалла /. В соответствии с (8.92) интенсивность 1_Ф должна быть такой, чтобы выполня­лось равенство + ^ = I® (0). На рис. 8.10 в виде штрихо­вых кривых приведены зависимости относительных величин

V4(0) и WM0) от ///вг при /вгАА=Ю. Заметим, что вследствие большого фазового рассогласования во вторую гар­монику из основных сигналов передается лишь очень небольшая доля мощности. С помощью (8.94) нетрудно показать, что пер­вый максимум величины [/2©//<а(0)] достигается при I — 1_С, где h (длина когерентности) определяется выражением (8.49).

В качестве второго примера рассмотрим решение уравнений (8.90) в случае, когда имеет место идеальный фазовый синхро­низм (Aft = 0). В этом случае может происходить довольно заметное преобразование во вторую гармонику и, следовательно,, необходимо учитывать истощение пучка на основной частоте* Таким образом, при решении уравнений (8.90) мы не можем те­перь полагать E^(z) = Е'_ф(0). Однако если М=0, то из уравне­ний (8.90) можно показать, что величина Е^г_ы является мнимой, а Е_т — вещественной. Иными словами, мы имеем

К = \^Ео^ ^--'1^1- (8.95а, б)

При этом уравнения (8,90) принимают вид

dz /_Вг £'_w (0)

_{<*|4о| 1 Up}

(8.96а)

(8.966)

Решения уравнений (8.96) с граничными условиями £^(/ = 0) = =Е'_а (0) иЕ'_ы (0) =0 записываются в виде

I^£L = £«(0)th(z//_Br)• | К*\ = К,(0) sch(z//_Bг). (8.97а, б)

Поскольку интенсивность волны пропорциональна | £" р, можно написать следующие соотношения: f,J/_(a (0) = I Е^г_ы \²/Е'^(0) и

IJ1_№ (0) = I £; \²/E'j0). Вычисленные" с помощью выраже- ний зависимости величии и от длины

кристалла представлены на рис. 8.10 в виде сплошных кривых.

Заметим, что когда / = /вг,. во вторую гармонику преобразуется значительная доля (-59%) падающей волны. Это наглядно

показывает роль /вг как характерной длины взаимодействия

второй гармоники. Ее величина обратно пропорциональна квад­ратному корню из интенсивности пучка на основной частоте [см. (8.91)1. Следует также заметить, что, когда / 3> /вг, излу­чение накачки в соответствии с соотношением Мэнли - Роу (8.92) может быть полностью преобразовано в излучение второй гармоники.