2.3.3.2. Неоднородное уширение

Предположим, что некий механизм уширения распределяет резонансные частоты атомов в некоторой полосе частот с цент­ром в Vo и что относительная плотность распределения этих частот равна g*(v'₀— v₀)> Согласно этому, g* (v^ — v₀) dv^f₀ есть

вероятность того, что резонансная частота атома попадает в интервал между и Vq+^Vq. Тогда из выражения (2.36а) или,

в более общем случае, из (2.47), если действует также какой-

либо другой механизм уширения (например, столкновительное

уширение), можно получить среднее значение коэффициентов

вынужденного излучения или поглощения. Таким образом,

²"⁸ I ц ?№ (v - v₀); (2.68)

_3/г⁸_в0А⁸

здесь через gt (v — v₀) обозначена функция

_{St — £* Wg [(v — v0) — х/ dfx,}

_(2.69)

—оо

причем x =v'₀ — v₀. Отсюда следует, что формула (2.39) остает- ся справедливой и в том когда присутствуют два меха- низма уширения: один однородный с формой линии g и другой неоднородной с формой линии g\ причем функция gt представ- ляет собой свертку этих двух функций. Если однородное уши- рение, описываемое функцией g (v — v'₀), много меньше неодно- родного уширения g* (y'_Q— v), то функцию g (v — v^) можно аппроксимировать б-функцией Дирака, и тогда

(2.70)

рассматривают

как полностью неоднород-

Этот случай иногда ное уширение.

В газах типичный механизм неоднородного уширения свя­зан с движением атомов и называется доплеровским ушире-нием. Чтобы проиллюстрировать этот тип уширения, рассмотрим

^{молекулу, которая в поле электромагнитного излуче-}

иия, имеющего частоту v (причем эта частота измеряется в лаб. системе координат). Обозначим через v составляющую ско­рости молекулы (измеряемую в той же лаб. системе координат)

в направлении распространения электромагнитной волны. Тогда частота волны v', измеряемая в системе координат движущего­ся атома, равна у' = v[l ±(vfc)] (эффект Доплера), причем

знак минус или плюс выбирается в зависимости от совпа­дают ли направления движения молекулы и распространения электромагнитной волны, или они направлены в противополож­ные стороны. Действительно, хорошо известно, что, если моле­кула движется навстречу волне, частота v', наблюдаемая в си­стеме координат атома, всегда больше частоты v, наблюдаемой в лаб. системе координат. Разумеется, при этом поглощение бу­дет происходить только тогда, когда частота v' электромагнит­ной волны в системе координат атома равна частоте атомного перехода vo, т. е. когда

v[l =fc (о/с)] «= v₀. (2.71)

Если переписать это выражение в виде

у = V₀/(l ± Vfc)_y

(2.72)

то мы придем к иной интерпретации процесса. А именно при рассмотрении взаимодействия электромагнитного излучения с

атомом результат будет тем же самым, как если бы атом был неподвиЖен, но имел резонансную частоту определяемую

^{выражением}

^vJ-VOitr/c),

(2.73)

_с

где vo — истинная частота атомного перехода. В самом деле, поглощение при такой интерпретации может происходить, когда частота v электромагнитной волны равна v' что согласуется

(2.72), если для v^r_u использовать выражение (2.73). С этой точки зрения можно сказать, что данный механизм уширения

^{действительно является неоднородным в смысле определения,}

данного в начале этого раздела. Чтобы вычислить соответствую­щую форму линииg* (y'_Q — v₀), достаточно вспомнить, что в газе,

находящемся при температуре Т, вероятность p_v dv того, что атом массой М имеет составляющую скорости между v и v + dv, дается распределением Максвелла

_{А (} ^М _У^/2_{~ (} ^М_**\й«

(2«74)

Поскольку из (2.73) следует, что

V —

К

(2.75)

v

О

то из выражений (2.74) и (2,75) получается искомое распреде­ление, если мы договоримся, что ff*(vj — v₀) dV₀= p_v dv. Таким

образом, мы получаем соотношение

v° Q/ J

(2.76)

v

2kT

О

_{£ (}^v_o^{— v}_o)⁼ _{— ( ) ехр —}

так что в случае чисто уширения в

с (2,70) контур линии запишется в виде

_{g (v — v0) = — 1 1 ехр — - я I.}

^v₀ ^{^ 2nkT ) L 2W v}₀ ^J

(2.77)

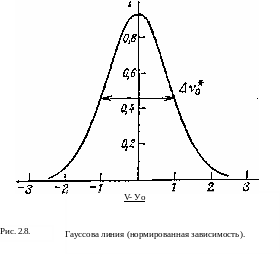
На рис. 2.8 изображена функция g*(v - v₀) = g*(Av) в зависи­мости от Av. Как и в случае лоренцевой кривой, максимум до­стигается в точке Av = 0, а ширина контура (доплеровская ши­рина линии) теперь равна

Av; = 4(lrln2)'».

(2.78)

Такая кривая называется через ширину линии Av*

_{шется в виде} гауссовой. Заметим, что выраженное максимальное значение g*(0) запи-

Av_n V я /

0,939

_о

_(2.79)

в то время как для лоренцевой кривой максимальное значе ние равНо

= = (2.80)

Av<

Следовательно, при данной ширине линии гауссова кривая за­острена сильнее лоренцевой.

Другим механизмом неоднородного уширения, приводящим опять-таки к гауссовой форме линии, может быть любое явле­ние, которое вызывает

случайное распределение JgCv-nM

частот атомных перехо­дов. Например, если ло­кальное электрическое поле кристалла случай­ным образом изменяется от точки к точке вследст­вие, скажем, дефектов кристаллической решет­ки, то благодаря эффекту

Штарка возникнут ло­кальные сдвиги энергети­ческих уровней, а вместе с ними и частот атомных переходов. Аналогичное явление имеет место так­же и в резупорядоченных

средах (таких, как стекло или жидкость), поскольку атомы,

^{окружающие рассматриваемый атом, распределены случайным}

образом. Что касается ширины линии, то она определеляется теперь среднеквадратичным отклонением локального электри­ческого поля.

По формуле (2.78) можно вычислить доплеровскую шири­ну линии AvJ = Дш*>/2я атома Ne при Т = 300 К на длине волны

К = 0,6328 мкм (одна из линий неона, на которой осуществля­ется лазерная генерация; см, гл. 6), которая оказывается рав­ной

AvJ=l,7 ГГц. (2.81)

Сравнение этой величины с соответствующими значениями, вы­численными для столкновительного [см. (2.66)1 и естественно­го уширений, показывает, что в рассматриваемом примере доп-леровское уширение значительно больше естественного, кото­рое в свою очередь существенно больше столкновительного. Это соотношение, впрочем, не всегда справедливо, поскольку при достаточно высоких давлениях газа столкновительное ушире­ние преобладает над доплеровским (например, в С0₂-лазере при атмосферном давлении; см, гл. 6).