8.3. Преобразование амплитуды: лазерное усиление [6—8]

В этом разделе мы рассмотрим работу лазерного усилителя с помощью скоростных уравнений. Допустим, что плоская волна постоянной интенсивности / падает (в точке z — 0) на лазерный усилитель длиной / вдоль оси г. Ограничимся рассмо­трением случая, когда падающее излучение имеет вид импульса

длительностью причем (т, где время

жизни нижнего, а т — время жизни верхнего уровня активной среды и W_p— скорость накачки усилителя. Это, по-видимому, наиболее подходящий набор условий, необходимых для лазер­ного усиления. Он применяется, например, когда нужно усилить импульс излучения Nd: YAG-лазера в режиме модуляции доб­ротности. Поэтому мы не бу-

дем здесь рассматривать случай непрерывного режи­ма усиления (стационарного

усиления), а читателю сове­туем обратиться к соответ­ствующей литературе [7, 8].

Сделав эти допущения, населенность нижнего уров­ня в усилителе можно поло­жить равной нулю, а накач­кой и релаксацией населен­ности верхнего уровня во время действия импульса можно пре­небречь. Тогда, используя выражение (2.82) (в котором мы по­лагаем F — I/hv), скорость изменения инверсии населенностей N'(t_rz) в точке 2 внутри усилителя можно записать в виде

где

dN/dt = —WN = - NI/T_Sf r_s=ftv/or

(8.23) (8.24)

— плотность энергии насыщения усилителя [см. (2.148в)]. Сле­дует заметить, что в (8.23) мы имеем дело с частной производ­ной, поскольку N должна быть функцией двух аргументов: z и t, т. е. Л^г = N(t_% z), вследствие того что 1 — 1(1, z). Получим теперь дифференциальное уравнение, описывающее временное и пространственное изменение интенсивности /. Для этого сначала вычислим скорость изменения плотности энергии р световой полны (где р — Пс, откуда dl/cdt = dp/dt). Рассматривая пол­ную скорость изм/нения энергии фотонов в малом объеме актив­ной среды усилителя (рис. 8.3), можно написать следующее

_{соотношение:}

1 д/ др / др\ /др\ (др\

_{с dt dt {dt Ji'^Kdt Л^У dth}⁹

(8,25)

где член (dp/dt) соответствует вынужденным излучению и по­глощению в усилителе, (др/<?/)₂— потерям в усилителе (напри­мер, потерям вследствие рассеяния) и (др/д1)х— полному по­току фотонов через объем. С помощью выражения (2,82) (пола­гая в нем F ~ I/hv) получаем

(dp/d/)i = WNhvaNL

Кроме того, из (2.82) и (2.86) следует, что

_{(др/д()-2~ — WaNahv= — а/;}

(8.26)

(8.27)

здесь N_a—плотность соответствующих центров потерь, W_a— вероятность поглощения и а — коэффициент поглощения в этих центрах. Для вычисления (др/dt) ₃ обратимся к рис. 8.3. Эле­ментарный объем активного вещества усилителя длиной dz с единичным поперечным сечением представлен заштрихованной областью. Величина (dp/dt) _zds- это скорость изменения энер­гии фотонов в элементарном объеме, обусловленная разностью между интенсивностями излучения на входе и выходе лазера,

_{т. е.}

(-37-) dz = I(t, z) — I(t, z + dz)

—

dl_ dz _dz.

(8.28)

При этом из выражений (8.25)-—(8.28) получаем следующее уравнение:

_{1 а/}

_{7^Г + ^7} ^{= <тЛ}_^-^а/_'

_(8.29)

которое вместе с (8.23) полностью описывает усиление лазера. Следует заметить, что это уравнение имеет обычный вид неста­ционарного уравнения переноса. Заметим также, что в непре­рывном режиме при а = 0 оно сводится к уравнению (1.7).

Уравнения (8.23) и (8.29) должны теперь быть решены с со­ответствующими граничными и начальными условиями. За на­чальное условие мы берем N (О, г) = No = const, где No опреде­ляется накачкой усилителя до появления лазерного импульса. Очевидно, что граничное условие задается интенсивностью h{t) светового импульса, который поступает в усилитель, т. е. / (t_% 0) = /о(/). При незначительных потерях в усилителе (т. е. в случае пренебрежения членом —а/) решение уравнений (8.23)

б'.Л*. Преобразование амплитуды

487

и (8.29) можно записать в виде

^{/ (г, т) — /}₀ ^{(т) \ 1 - [1 — ехр (— а}_я^{г)]ехр ^— J /}₀ ^{(т') ^т'/Г^ | ,}

(8.30)

_{где т =} t — г/с, a a_g = 0JV_o— коэффициент ненасыщенного уси­ления усилителя. Из уравнения (8.29) нетрудно получить также выражение для полной плотности энер­гии лазерного излучения:

-|-00

(8.31)

_{Г (z)}

₌ ^С _{I (г, 0 dt.}

J

Интегрируя обе части уравнения (8.29) по времени от t = —оо до t = +Д и ис­пользуя соотношение (8.23), получаем

dr/dz= а_аГ_а[\ - ехр (- T/T_s)]-aГ. (8.32)

— ОО

Отсюда, снова пренебрегая потерями усилителе, находим

_в

_{Г (/) = TS In {1 + [мр (Гвх/Г,) - 1] G0};}

мирована на плотность энергии насыщения ла­зера =

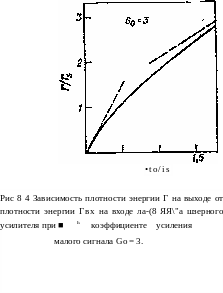
здесь Go = ехр (a_gl)— ненасыщенное уси­ление усилителя, а Г_вх — плотность энер­гии входного пучка. В качестве характер­ного примера на рис. 8.4 построена кри­вая зависимости отношения Г/Г₈ от

Гвх/Г,₅ при Go=3, Заметим, что в случае Гщ^Гя выражение (8.33) можно записать приближенно в виде

^{р — (?}₀^Г

^/J5.34)

т. е. выходная плотность энергии растет линейно с входной плот­ностью (режим линейного усиления). На рис. 8.4 построена

также зависимость, описываемая выражением (8.34), в виде

штриховой прямой, выходящей из начала координат. Однако из рисунка мы видим, что при больших входных плотностях ве­личина Г увеличивается с ростом Г_вх с более низкой скоростью, чем предсказывает выражение (8.34), т. е. происходит насыще­ние усилителя. При Г_вх > Г.? (режим насыщения) получаем

Г(/)= Гвх +I>J.

(8.35)

На рис. 8.4 построена также прямая, вычисленная но формуле (8.35) и представленная второй штриховой линией. ЗаметиМ, Что

при больших входных плотностях энергии выходная плотность

энергии линейно зависит от длины / усилителя. Поскольку Vsttgl = N₀lhv, каждый возбужденный атом испускает вынужден­ное излучение и, таким образом, вносит свой вклад в энергию пучка. Такое условие, очевидно, соответствует наиболее эффек­тивному преобразованию запасенной энергии в энергию пучка; поэтому во всеХ тех случаях, в которых это практически осуще­ствимо, используются конструкции усилителя, работающего в ре­жиме насыщения.

Если усилитель имеет потери, то рассмотренная выше кар­тина несколько изменяется. В частности, плотность выходной энергии Г(/) теперь не увеличивается непрерывно с ростом входной (как на рис. 8.4), а достигает максимума и затем умень­шается. Это можно понять, если заметить, что выходная плот­ность как функция длины усилителя имеет тенденцию увеличи­ваться линейно за счет усиления [по крайней мере при больших

входных плотностях энергии; см. (8.35)] и убывать экспонен­циально за счет потерь [из-за члена —аГ в (8.32)1. Конкурен­ция этих двух величин дает максимальное значение выходной

плотности энергии Г, которая в случае а <С a_g записывается в виде

Г ~ a_gTJa. (8.36)

Однако, поскольку усилитель, как правило, имеет небольшие

потери, максимальное значение плотности энергии, которое мо­жно получить от усилителя, ограничивается другими явлениями.

В действительности плотность энергии ограничивается значе­нием при котором усилитель разрушается (в некоторых прак­тических случаях T_d ~ 10 Дж/см²). Таким образом, из (8.35) получаем

Однако коэффициент усиления

нельзя делать слишком большим, поскольку иначе в усилителе

могут возникнуть два таких нежелательных эффекта, как пара­зитная генерация и усиленное спонтанное излучение (УСИ). Па­разитная генерация возникает, когда усилитель начинает генери­ровать вследствие обратной связи, которая до некоторой степени

всегда существует (например, благодаря наличию отражения

на торцах усилителя . Явление УСИ уже рассматривалось нами в разд. 2.7.3. Оба этих явления имеют тенденцию снимать имеющуюся инверсию и вследствие этого уменьшать усиление лазера/ Чтобы свести к минимуму паразитную генерацию, не следует использовать усилители большой длины. В идеальном случае усилитель должен иметь приблизительно одинаковые раз­меры во всех направлениях. Однако даже в этом случае пара­зитная генерация устанавливает верхний предел (а^/)_макс для произведения коэффициента усиления a_g на длину усилителя /, т. е.

a_gl < (а₅/)макс- (8.38)

В практически реализуемых случаях величина (а^/)_Макс имеет значения 3—5. В разд. 2.7.3 [выражение (2.153)] мы уже опре­делили порог для УСИ. Если усилитель имеет форму куба (т. е. лри Q ж 1), то G ж 5,1 (или a_gl ж 1,6), т. е. величину того же порядка, что и величина, определяемая паразитной генерацией. При меньших значениях телесного угла Q (что обычно имеет место) величина G, определяющая начало действия УСИ, увели­чивается [выражение (2.153)]. Следовательно, достижение мак­симально возможного коэффициента усиления определяется, как правило, паразитной генерацией, а не УСИ. Учитывая ограниче­ния, связанные как с разрушением усилителя [(8.37)], так и с паразитной генерацией [(8.38)], нетрудно получить выраже­ние для максимальной энергии Е_т, которую можно выделить из усилителя:

т dm й \ g )_т! g*

где 1_т — максимальный размер усилителя (в форме куба), опре­деляемый формулой (8.38). Из выражения (8.39) следует, что Е_т увеличивается с уменьшением коэффициента усиления а#. Уменьшение величины a_g в конечном счете ограничивается по­терями усилителя а. Выбирая, например,

«10*"²см~¹ и r_rf = 10 Дж/см², из (8.39) получаем Е_т ж 1 МДж Однако при этом размер усилителя должен быть порядка 1_т ж tt(agl)_ma_e&3 м, что практически довольно трудно реали­зовать,

В данном разделе до сих пор нас интересовало главным об­разом изменение энергии лазерного импульса при его прохожде­нии через усилитель. Однако в режиме насыщения существен­ные изменения претерпевают также временное и пространствен­ное распределения входного пучка. Пространственные искажения нетрудно объяснить с помощью рис. 8.4. В случае когда про­филь интенсивности входного пучка в поперечном сечении имеет колоколообразную форму (например, гауссов пучок), централь­ная область пучка вследствие насыщения будет усиливаться

меныие, чем периферическая. Таким образом, по мере того как пучок проходит через усилитель, ширина его пространственного распределения в поперечном сечении увеличивается. Совсем не­трудно показать, почему пучок испытывает и временные иска­жения. Вынужденное излучение, вызванное передним фронтом импульса, приводит к тому, что к моменту появления заднего фронта импульса из усилителя была уже извлечена некоторая часть запасенной энергии. Таким образом, когда задний фронт импульса проходит через усилитель, инверсия населенностеи в усилителе оказывается пониженной и, следовательно, пучок ис­пытывает меньшее усиление. Вследствие этого в задний фронт импульса вкладывается меньше энергии, чем в передний, что ведет к довольно заметному изменению формы импульса. Форму выходного импульса можно вычислить из выражения (8.30), от­куда можно показать, что в зависимости от формы входного импульса выходной импульс может либо расшириться, либо су­зиться (или даже остаться неизменным) [6].

В заключение этого раздела мы кратко ознакомимся с двумя другими примерами лазерного усиления в условиях, отличаю­щихся от рассмотренных выше. В первом случае предполагают, что длительность %_р импульса, который необходимо усилить, много меньше времени жизни атомов на нижнем энергетическом уровне лазера ^х\ Это имеет место, например, в случае лазер­ного усилителя на рубине, в котором нижний уровень совпадает с основным состоянием. Аналогичная ситуация возникает также в усилителе на ионах Nd³⁺, когда т_р < 1 нс. В обоих случаях усилитель работает по трехуровневой схеме. Нетрудно показать, что приведенные выше формулы остаются справедливыми, но

при условии, что дастся теперь выражением

^hv/2a.

(8.39а)

Ко второму случаю (мы его кратко обсудим) относится усили­тель, в котором как верхний, так и нижний уровни состоят из множества сильно связанных между собой подуровней. Это имеет место, например, в усилителях на С0₂ или HF, в которых верхние и нижние (колебательные) уровни состоят из многих вращательных подуровней (см., например, рис. 6.16), Если дли­тельность импульса много больше, чем время релаксации между вращательными подуровнями, то между ними будет поддержи­ваться равновесное тепловое распределение населенностеи. При этом населенность NJ вращательного подуровня, принадлежа­щего данному колебательному уровню, может быть представ­лена как доля г суммарной населенности N колебательного уро-

*> Однако мы будем считать, что х_Р > Г₂, где Тч = 1/jtAv₀, поскольку это условие необходимо для того, чтобы было справедливым приближение скоростных уравнений (см. разд. 5.5).

вня (см. разд. 2,8), причем величину г (статистическая сумма) можно вычислить/используя статистику Больцмана. Кроме того, предположим, что длительность импульса т_р значительно мень­ше времени релаксации нижнего уровня лазера (т. е. система фактически ведет себя как трехуровневая) и что длина волны входящего светового импульса соответствует только одной вра-щательно-колебатсльной линии. В этом случае будут справед­ливы все полученные выше выражения, но при условии, что [8]

T_s = hv/2oz_i (8.396)

где а — сечение вынужденного излучения того вращательно-ко-леб а тельного перехода, на котором происходит процесс усиле­ния. Сравнивая выражения (8.396) и (8,39а), мы видим, что эффективное сечение можно определить как га [см, также выра­жения (2.170а) и (2Л706)]. В случае когда длительность им­пульса оказывается сравнимой с временем вращательной релак­сации, картина становится намного более запутанной и вычис­ления с помощью соответствующих уравнений требуют, вообще говоря, применения ЭВМ [8].