7.6. Направленность

Свойство направленности лазерного пучка тесно связано с его пространственной когерентностью. Поэтому сначала мы об­судим электромагнитную волну с полной пространственной ко­герентностью, а затем с частичной.

7.6.1. Пучки с полной пространственной когерентностью

Рассмотрим сначала волну с полной пространственной коге­рентностью, образованную пучком с плоским волновым фронтом кругового поперечного сечения, имеющим постоянную интенсив­ность по сечению (рис. 7.5, а). Вследствие дифракции такой пу­чок характеризуется углом расходимости Дифракционную

Рис. 7,5. а - расходимость (обусловленная дифракцией) пучка электромаг­нитного излучения с плоским волновым фронтом, круговым поперечным се­чением и равномерным распределением интенсивности в поперечном сечении; б — метод измерения расходимости плоской волны, показанной иа рис. а.

расходимость пучка можно понять из рис. 7.5, а, на котором изображен волновой фронт Л'В', полученный из волнового фрон­та АВ с помощью принципа Гюйгенса - Френеля. Можно пока­зать, что расходимость 0^ дается выражением

e_d = l,22X/£>, (7.43)

где D — диаметр пучка. Чтобы понять, откуда берется расходи­мость, давайте выясним, что произойдет, когда рассматривае­мый нами пучок фокусируется с помощью линзы (рис. 7.5,6). Поскольку, как мы уже видели, пучок имеет некоторую ширину, можно показать, что его можно представить в виде набора плоских волн, распространяющихся в несколько различных на­правлениях. Одна из них, распространяющаяся под углом в к оси, показана на рис. б штриховыми линиями. КаК мы ви­дим, эта волна будет фокусироваться в фокальной плоскости линзы в точке Р, которая отстоит (при малых значениях угла 8)

^{от оси пучка на расстояние}

г = /6. (7.44)

Таким образом, зная распределение интенсивности 1(г) в фо­кальной плоскости, можно найти угловое распределение исход­ного пучка. Из теории дифракции из­вестно [3, с. 395—398], что функция Г (г) дается формулой Эйри:

^{, _ Г 2/, (krD/2f) р .} ₍₇ ^.«

где k = 2п/к, /, — функция Бесселя первого порядка, а /о (интенсивность в центре фокального пятна) равна

-щт ) ■ (7.46)

Здесь Pi — мощность пучка, падающе­го на линзу.

На рис. 7,6 приведена зависимость интенсивности / от величины

_{х = krD/2f. (7,47)}

Следовательно, дифракционная карти­на, создаваемая в фокальной плоско­сти линзы, состоит из круглой цент­ральной зоны (диск Эйри), окружен­ной рядом колец с быстро убывающей интенсивностью. Расходимость Q_d исходного пучка обычно опре­деляется как угловой радиус первого минимума, показанного на

рис. 7.6. Таким образом, из рис. 7.6 и выражений (7.47) и

(7.44) получаем соотношение (7.43). при этом можно показать, что выражение (7.43) для 0, имеет некоторую неопределенность.

В качестве второго примера распространения пространствен­но-когерентного пучка рассмотрим гауссов пучок (ТЕМоо), кото­рый можно получить с помощью устойчивого лазерного резона­тора со сферическими зеркалами. Если шо — размер пятна в перетяжке пучка, то размер пучка w и радиус кривизны i? вол­новой поверхности на расстоянии _z от положения перетяжки можно найти, воспользовавшись соотношениями (4.105) и (4.106).

Чтобы вычислить расходимость гауссова пучка, рассмотрим вы­ражения (4,105) и (4.106) на большом расстоянии от перетяжки (т. е. при условии kzjnwl^> 1). Мы видим, что на больших рас­стояниях w = ХгДшо и R = 2. Поскольку на больших расстоя­ниях оба параметра w и R линейно растут с расстоянием, мы практически имеем сферическую волну, испущенную из центра

Рис. 7.7. Относительная доля полной мощности данной моды ТЕМ*, _да, кото-

да^J

рая заключена в пределах круглой апертуры радиусом г. Здесь w — размер пятна моды ТЕМоо и числа возле каждой кривой соответствуют модовым

индексам I, т.

перетяжки. Ее расходимость может быть найдена из выражения

Q_d = w/г = К/пщ. (7.48)

Сравним теперь выражения (7.48) и (7.43). Если при этом поло­жить D — 2шо, то при одинаковых диаметрах расходимость гаус­сова пучка оказывается в два раза меньше расходимости пло­ского пучка.

Рассмотрим гауссову моду высшего порядка Чтобы

вычислить ее расходимость, необходимо определить эффектив­ный размер пятна wt, _т этой моды. Это можно осуществить с помощью рис. 7.7, на котором представлены расчетные значе­ния относительной доли полной мощности для каждой поперечной моды, заключенной в пределах круглой апертуры радиусом г. Радиус г нормирован на ш — размер пятна моды ТЕМоо в пло­скости апертуры. Теперь мы можем определить эффективный размер пятна Wi_ttn как радиус пятна, в пределах которого за­ключено, например, 90 % мощности пучка. Этот размер пятна

_{можно записать в виде}

_{Wl, m=} ^c_{i, «а».}

_(7.49)

где С/, ж—численный коэффициент, который всегда больше 1 и зависит от модовых индексов / и m и значение которого нетруд­но найти из рис. 7.7. Заметим, что в соответствии с данным оп­ределением коэффициент С₀, о - 1,16 и эффективный размер пятна моды ТЕМоо равен приблизительно 1,16». Кроме того, эффективный размер пятна возрастает с увеличением модовых индексов I и т. Определим расходимость пучка как

^{6/,m = Hm wt}₉^Jz*=Ci_{9 m} ^{Нт w/z;}

(7.50)

здесь использовано соотношение (7.49). Поскольку на больших расстояниях от положения перетяжки w ~ Xz/nwo, то выраже­ние (7.50) принимает вид

(7.51)

откуда следует, что расходимость гауссовой моды высшего по­рядка всегда больше, чем у моды ТЕМоо. Заметим, что согла­сно выбранному определению эффективного размера пятна рас­ходимость моды ТЕМоо будет примерно в 1,16 раза больше, чем это следует из выражения (7.48). Кроме того, если мы опреде­лим эффективный размер цятна ш₀₎о моды ТЕМоо в плоскости

перетяжки пучка как w₀,o = 1,16 ш₀, то расходимость пучка этой

моды можно представить как 8о,о = 1,16Х/яшо = (1,16)²Л/ше>.о,о.

Подводя итог полученным результатам, можно сказать, что расходимость 9а пространственно-когерентной волны можно за­писать в виде

^{0^ — PPw^1~)}

(7.52)

где D — соответствующим образом определенный диаметр пучка и р — числовой коэффициент порядка единицы, точное значение которого зависит от распределения амплитуды поля, а также от

способа, которым определены значения Ва и D. Такой пучок обычно называется дифракционно-ограниченным.

7.6.2. Пучки с частичной пространственной когерентностью

Примеры, иллюстри-_____ различные свойства расходимости когерентной и частично-когерентной воли. а - пучок диаметром D пред­ставляет собой суперпозицию множества меньших по разме­ру когерентных пучков диа­метром % .-пучок диамет­ром D и область когерентно­сти А_с в точке Р.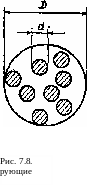

Расходимость электромагнитной волны с частичной прост­ранственной когерентностью больше, чем у пространственно-ко­герентной волны, имеющей такое же распределение интенсивно­сти. Это можно понять, например, из рис. 7.5, а: если волна не является пространственно-когерентной, то вторичные волны, из­лученные с поперечного сечения АВ_% не должны больше нахо­диться в фазе и волновой фронт, образованный вследствие диф­ракции, должен иметь большую рас­ходимость по сравнению с той, ко­торая получается из выражения (7.43). Строгое рассмотрение этой задачи (т. е. задачи о распростране­нии частично-когерентных волн) вы­ходит за рамки настоящей книги, и читателю мы рекомендуем обратить­ся к более специализированным книгам [3, с. 508—518]. Мы же ограничимся изучением относитель­но простого случая пучка диамет­ром D (рис. 7.8, а), который состоит

из множества пучков (показанных

на рисунке в виде заштрихованных кружков) меньшего диаметра d. Бу­дем предполагать, что каждый из этих пучков меньшего диаметра яв­ляется дифракционно-ограниченным

взаимно целом будет равна Q_d = $X/d. Если бы такие пучки были коррелированными, то рас­ходимость была бы равна B_d = фк/D. Этот последний случай фактически эквивалентен множеству антенн (маленьких пуч­ков), которые все излучают синхронно друг с другом. После этого простого примера можно рассмотреть общий случай, когда

пространственно-когерентный пучок имеет данное распределе­ние интенсивности по его диаметру D и данную область коге­рентности А_с в каждой точке Р (рис. 7.8, б). По аналогии с пре­дыдущим примером нетрудно понять, что в этом случае

^{-PVHcJI/8, где р-числовой коэффициент порядка единицы,}

^{значение которого зависит как от конкретного распределения}

интенсивности, так и от способа, каким определялась область Ас Таким образом, понятие направленности тесно связано с по­нятием пространственной когерентности.

(т. е. пространственно-когерент­ным). Тогда, если составляющие пучки ваны, расходимость всего пучка в

После общих замечаний о пучке с частичной пространствен­ной когерентностью мы можем перейти к рассмотрению особен­но важного случая лазерной генерации на многих поперечных модах. Таким образом, мы рассмотрим устойчивый лазерный ре­зонатор, в котором поперечный размер 2а активной лазерной среды значительно больше размера пятна моды ТЕМоо, распро­страняющейся внутри этой среды. Соответствующими примера­ми могут быть непрерывный или импульсный твердотельные ла­зеры, поэтому мы можем обратиться к случаю, показанному на рис, 5.14. Однако последующее рассмотрение применимо вообще к любому многомодовому лазеру с устойчивым резонатором. Для простоты предположим, что размер пятна w в среде при­близительно равен размеру пятна Wq в перетяжке пучка. По­скольку радиус а существенно больше, чем Wq, следует ожидать, что будет возбуждено много поперечных мод, которые заполнят поперечное сечение лазерной среды. Предполагается, что возбу­ждаемая мода высшего порядка ограничена до размера» кото­рый незначительно обрезаается апертурой среды Поперечные индексы этой моды можно найти из рис. 7.7, если известны мак­симально допустимые потери возбуждаемой моды. Предполо­жим, например, что эти потери равны 10 %, тогда 90 % мощно­сти этой моды высшего порядка должно проходить через лазер­ную апертуру. В этом случае эффективный размер пятна Wi,_m в соответствии с определением, данным в предыдущем разделе, должен быть равен радиусу а среды, т. е, Wi_{% т} = а, С помощью выражения (7.49) получаем

a = Ci_}mw=Ci_imw₀. (7.53)

При данных значениях а и ш₀ выражение (7.53) позволяет вы­числить коэффициент С/, _т, который затем можно использовать в выражении (7.51), чтобы найти расходимость моды. Посколь­ку эта мода имеет самую большую расходимость, ее можно гру­бо оценить по полной расходимости пучка в^, предполагая, что она равна расходимости этой моды 8*, _т. Из выражений (7.51) и (7.53) получаем

8. ~ аШт\ (7.54)

ь* - «

Выражение (7.54) полезно в ряде случаев. Если известен раз­мер шо, то его можно использовать для оценки ожидаемой рас­ходимости многомодового лазера. Если размер w₀ не известен, а расходимость Q_d измерена, то из (7.54) можно получить оцен­ку wq. Заметим, что в соответствии с выражением (7.54) расхо­димость пучка многомодового лазера увеличивается с увеличе­нием апертуры а резонатора и уменьшением размера пятна Wq

моды ТЕМоо-

Выходной пучок

От данной некогерентной лампы S можно получить простран­ственно-когерентную волну, а именно существенно снизить ее расходимость, если использовать устройство, изображенное на рис. 7.9. Свет от лампы S фокусируется на небольшой диафраг­ме диаметром d₉ расположенной в фокальной плоскости линзы I/.Свет, прошедший через эту диафрагму, будет заполнять боль­шой конус углов (сплошные линии на рис. 7.9), соответствую­щий фокусирующему конусу линзы L. Однако пучок, образую­щийся в результате дифракции на этой диафрагме, имеет зна­чительно меньшую расходимость 6=l,22X/d и будет таким образом занимать область, которая на рис. 7.9 заштрихована.

Рис. 7.9. Метод получения когерентного пучка от некогерентиого источника