7,4. Статистические свойства лазерного излучения и излучения тепловых источников

Прежде чем приступить к рассмотрению когерентных свойств световых пучков, следует сравнить статистические свойства ла­зерного излучения и излучения обычных источников света.

Рассмотрим лазер, генерирующий в непрерывном режиме из­лучение на одной поперечной и продольной моде. Как уже отме-

ч алось в разд. 5.3.1, при данной скорости накачки интенсивность выходного излучения такого лазера определяется из условия, со­гласно которому переходы на нижние уровни вниз, обусловлен­ные вынужденным излучением, должны быть в точности ском­пенсированы переходами на верхние уровни, вызванными на­качкой. Мы также указали на то, что интенсивность выходного излучения подвержена в очень

^{флуктуа-}

_{спонтан-}

небольшой степени циям, связанным со ным излучением. Таким обра­зом, можно считать, что шири­на полосы генерации одномо-дового лазера преимуществен­но обусловлена флуктуациями фазы фЦ)₉ а не флуктуациями

^{амплитуды лазерного поля.}

Эти флуктуации вызваны либо флуктациями фазы за счет спонтанного излучения, либо, что встречается чаще, измене­ниями длины резонатора вслед­ствие теплового расширения

или вибраций со звуковой ча­стотой. Это означает, что если мы запишем аналитический сигнал V(t) в данной точке

^{пространства в виде}

V(t)-Е (0 ехр {/[£(/)

_(7.8)

то относительные амплитудные флуктуации величины E(t)_f равные ]dE/Edt\,будут МНОГО меньше, чем изменения фазы

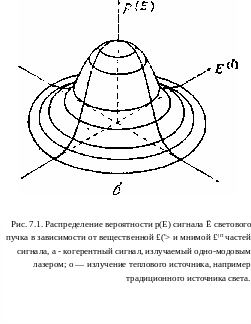
\ф\. Теперь МОЖНО воспользо­ваться очень полезным трех­мерным представлением, в ко­тором вероятность измерения данного значения величины V вы­ражается через вещественную и мнимую части, соответственно £<о и £<*> фазора E(t) = Е(t)ехр [#(f)J.Поскольку флуктуации амплитуды очень малы, данное представление будет иметь вид, показанный на рис. 7.1, а. Заметим, что величина р(Е) на этом рисунке означает, что произведение p{E)dE^dE^ дает элемен­тарную вероятность того, что измеренная величина £<^г> будет находиться между значениями £^{г> и Eⁱⁿ+ dE^\измеренная ве­личина £⁽ⁱ⁾ — между £⁽⁰ и E^-j-dE^h Иными словами» величина р (Е) (Е dE йф) есть вероятность того, что измеренные значения величины £ находятся в интервале от Я до Е + d£, а измерен­ные значения величины Ф — от $ до Ф + d&. Заметим, что флук­туации амплитуды Ё =Е{t) представлены на рисунке в сильно увеличенном масштабе. На самом деле для лазера, работающего несколько выше порога генерации, распределение вероятности р(Е) можно написать в виде

р(£)~6(£~-£₀), (7,9)

где б — функция Дирака, a £о связано с интенсивностью пучка

/ в соответствии с (7.7) и (7.8) выражением Е% = /. Таким обра­зом, точка, которая описывает E(t) в плоскости фазора, будет

по существу перемещаться во времени по окружности радиусом

\Е\ = Ео. Благодаря статистической природе флуктуации фазы это движение будет иметь вид случайного блуждания, угловая скорость которого, выраженная через фазовый угол ФЦ), опре­деляет ширину полосы лазерной генерации.

Свет же от обычной лампы можно рассматривать как су­перпозицию некоррелированных световых волн, испущенных спонтанно атомами вещества. Заметим, что поскольку такое из­лучение происходит по существу в условиях теплового равнове­сия, его называют тепловым. В этом случае, поскольку число таких некоррелированных излучателей очень велико, согласно центральной предельной теореме статистики распределение ам­плитуды вещественной и мнимой частей величины Е должно

подчиняться закону Гаусса. Таким образом, мы имеем р(Е) ~ ~ ехр— [Е²/С], где С — постоянная, которая, как нетрудно за­метить, равна средней интенсивности пучка </>. Согласно опре­делению интенсивности /, данному в выражении (7.7), можно

^{показать, что </> = J J Е2р (Е) (Е dE dfjД J р (Е) (Е dE dj>) =}

= [ Е²р (Е) dE² I \ р(Е) dE² = С. Таким образом, р (£) можно записать в виде

р(Е)~ехр{ — &/(!)). (7.1.0)

Эта функция построена на рис. 7Л, б в зависимости от вещест­венной и мнимой частей поля E(t). Заметим, что теперь средние значения как £^(г), так и £^(/) равны нулю, в то время как сред­нее значение величины £² точно равно интенсивности пучка. В плоскости £<^г), £^(/) движение точки, которая описывает вели­чину £(г), можно рассматривать как случайное блуждание от­носительно начала координат. Скорость этого движения,

женная через изменения амплитуды и фазы (dE/E dt и d<f>/dt соответственно), определяет ширину полосы излучения тепло­вого источника света.

Сравнение рис. 7.1, а и 7.1, б делает наглядным глубокое раз­личие между лазерным и тепловым излучением,