
Петро, Василь та Микола
Три грибники, Петро, Василь та Микола, повертаючись з лісу додому, вирішили влаштувати привал, а заодно і перекусити. Як це у нас прийнято, через певний час кожен почав вихвалятись своїми сьогоднішніми успіхами, а з часом і ділитись знайденими грибами зі своїми товаришами. Перед привалом у кожного з них була певна цілочислова кількість грибів. Спочатку Петро дав Василю та Миколі по стільки грибів, скільки у них вже було. Микола швидко зрозумів, що так буде не по-братськи, і дав Василю та Петру по стільки грибів, скільки у них стало. Василь не міг відстати від співтоваришів і також дав кожному з друзів по стільки грибів, скільки у них на цей моменту було у наявності. І тут друзі з подивом виявили, що у всіх стало грибів порівну. Скільки грибів було у кожного перед привалом, якщо відомо, що всі разом вони зібрали N грибів?
Введення-виведення.
У єдиному рядку знаходиться єдине натуральне число N (N ≤ 30000).
У єдиному рядку вивести через пропуск кількість грибів перед привалом у Петра, Василя та Миколи відповідно.
Приклад.
Введення: 120
Виведення: 65 20 35
var
n,P,V,M:Integer;
begin
Readln(n);
P:=13*n div 24;
V:= 4*n div 24;
M:=7*n div 24;
Writeln(P,' ', V,' ',M,' ');
end.
8. НСД і НСК
Дано два цілі числа. Знайдіть їх найбільший спільний дільник та найменше спільне кратне.
Введення-виведення.
Ввести два цілі числа. Вивести через пробіл НСД та НСК.
Приклад.
Введення: 4, 6
Виведення: НСД=2 НСК=12.
Розв’язок
var a,b,k,nsd,nsk:real;
begin
read(a,b);
k:=a*b;
while a<>b do
if a>b then a:=a-b
else b:=b-a;
nsd:=a;
nsk:=k/nsd;
writeln('НСД=',nsd,' ','НСК=',nsk);
end.
9. Ділення на 3
Як відомо, число ділиться на 3 (без остачі) тоді і тільки тоді, коли сума його цифр ділиться на 3 також без остачі. Перевірьте цю ознаку подільності на 3 на прикладі заданого трицифрового числа.
Приклад 1. Приклад 2.
Введення: 1 1 1 Введення: 1 1 0
Виведення: ділиться Виведення: не ділиться.
Розв’язок
var a,b,c,k:longint;
begin
read(a,b,c);
k:=a+b+c;
if (k mod 3=0) then writeln('дiлиться')
else writeln('не дiлиться');
end.
Завдання 3. Гуси та кролі
У гусей та кролів разом n лап (n – парне). Скільки може бути гусей та кролів (вивести всі можливі поєднання)?
Введення: 10
Виведення: гусей 1 кролів 2
Гусей 3 кролів 1
Розв’язок
var n,a,a1,a2,b,b1:integer;
begin
read(n);
a:=n mod 4;
a1:=a div 2;
a2:=n div 4;
b:=n-4;
b1:=b div 2;
writeln('гусей ',a1,' ','кролiв ',a2);
writeln('гусей ',b1,' ','кролiв 1');
end.
10. Годинник
Ім'я вхідного файлу: |
clock.dat |
Ім'я вихідного файлу: |
clock.sol |
Максимальний час роботи на одному тесті: |
1 секунда |
Максимальна оцінка за завдання: |
20 балів |
Старовинний годинник б'є щопівгодини. Причому на початку кожної години він б'є стільки раз, скільки годин (по 1 разу – в час ночі і в час дня, по 2 рази – в дві години ночі та в дві години дня і так далі, опівночі і опівдні вони б'ють, відповідно, по 12 разів). І ще 1 раз вони б'ють в середині кожної години.
Даний проміжок часу (відомо, що пройшло строго менше 24 годин). Напишіть програму, що визначає, скільки ударів зробив годинник за цей час.
Формат вхідних даних
У першому рядку записаний початковий момент часу, в другому рядку — кінцевий. Моменти часу задаються двома цілими числами, що розділяються пропуском. Перше число задає години (від 0 до 23), друге - хвилини (від 1 до 59, при цьому воно не дорівнює 30).
Формат вихідних даних
У вихідний файл виведіть одне число — скільки ударів зробив годинник за цей відрізок часу.
Приклади
clock.dat |
clock.sol |
5 20 10 25 |
45 |
10 25 5 20 |
135 |
5 2 5 21 |
0 |
Розв’язок перший: моделювання. “Крутитимемо” стрілки годинника, кожну хвилину оцінюючи ситуацію і рахуючи удари. Цей алгоритм можна реалізувати, наприклад, так.
while (h1 <> h2) or (m1 <> m2) do begin
inc(m1); {додаємо одну хвилину}
if m1 = 60 then begin
inc(h1); h1 := h1 mod 24; m1 := 0;
if h1 mod 12 = 0 then
inc(res, 12)
else
inc(res, h1 mod 12);
end
else
if m1 = 30 then
inc(a);
end;
(тут h1:m1 – початковий час, h2:m2 – кінцевий час, res – кількість ударів).
Розв’язок другий: підрахунок ударів. Хай початковий час менше кінцевого. Тоді можна підрахувати кількість ударів таким чином. Загальна кількість ударів складається з
“годинних” ударів в моменти часу (h1+1):00, (h1+2):00, ., h2:00;
“півгодинних” ударів в моменти часу (h1+1):30, (h1+2):30, ., h2:30;
“півгодинного” удару у момент часу h1:30, якщо m1<30;
“півгодинного” удару у момент часу h2:30, якщо m2>30.
Тепер відмітимо, що за добу годинник б'є 180 разів. Тому у разі, коли кінцевий час менше початкового, можна поміняти їх місцями, обчислити кількість ударів за приведеною вище схемою і відняти отримане число з 180.
Розв’язок третый: явна формула. Позначимо через U(t1,t2) кількість ударів в проміжок часу [t1,t2]. Тоді
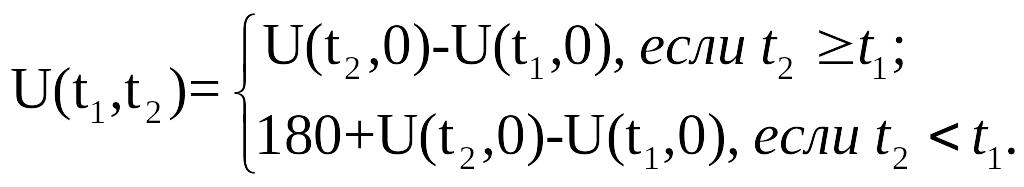
Для величини U(t,0) теж можна вивести явну формулу. Наприклад, таку:
U(h:m,0)= (h DIV 12) * 78 + {Кількість “годинних” ударів
за повних 12 годин }
+ (h MOD 12) * ((h MOD 12) + 1) DIV 2
{кількість “годинних” ударів
за останній час }
+ h {кількість “півгодинних” ударів}
+ ord (m > 30) {ще один “півгодинний” удар
якщо m>30 }
