Лабораторной работе № 1 Исследование разомкнутой линейной систем
Вариант 8
Описание системы
Исследуется система, описываемая математической моделью в виде передаточной функции
n=[1.7 1.36 0.204];d=[1 1.1857 0.7673 0.4592]; f = tf ( n, d )
Transfer function:
1.7 s^2 + 1.36 s + 0.204
-----------------------------------
s^3 + 1.186 s^2 + 0.7673 s + 0.4592
2. Результаты исследования
нули передаточной функции
-0.6000
-0.2000
полюса передаточной функции
-0.9000
-0.1428 + 0.6999i
-0.1428 - 0.6999i
коэффициент усиления звена в установившемся режиме
k = 0.4443
полоса пропускания системы
b =5.4554 рад/сек
модель системы в пространстве состояний
a =
-1.186 -0.3836 -0.4592
2 0 0
0 0.5 0
b =
2
0
0
c = 0.85 0.34 0.102
d = 0
статический коэффициент усиления после изменения матрицы
k1 = 0.4443
связь между k
и k1
объясняется тем, что при
нахождении статического коэффициента
передачи через модель в пространстве
состояний мы используем формулу (
),
в которой есть слагаемое D.
Оно в рассматриваемом нами случае
системы с одним входом и одним выходом
просто скалярная величина, значение
которой мы изменили с нуля на единицу.
модель исходной системы в форме «нули-полюса».
1.7 (s+0.6) (s+0.2)
---------------------------------
(s+0.9) (s^2 + 0.2857s + 0.5102)
коэффициенты демпфирования и частоты среза
-
Полюс передаточной функции
Собственная частота, рад/сек
Постоянная времени, сек
Коэффициент демпфирования
-0.9000
-0.1428 + 0.6999i
-0.1428 - 0.6999i
0.2000
0.2000
0.1000
5
2
2
1.0000
0.2000
0.2000
Импульсные характеристики систем f и f_ss получились, одинаковые, потому что для модели f_ss (
)
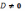импульсная характеристика построена
неправильно, так как в момент времени
t=0
она должна быть бесконечной по величине,
и система Matlabв
таком случае строит импульсную
характеристику для строго правильной
части, принимая
,
т. е. для модели f.
Переходные процессы исходной и модифицированной систем
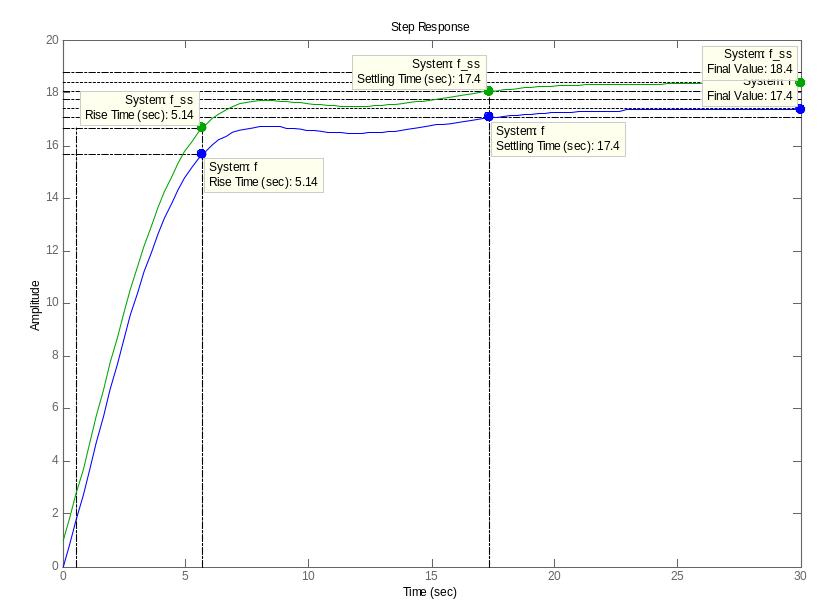
амплитудная частотная характеристика
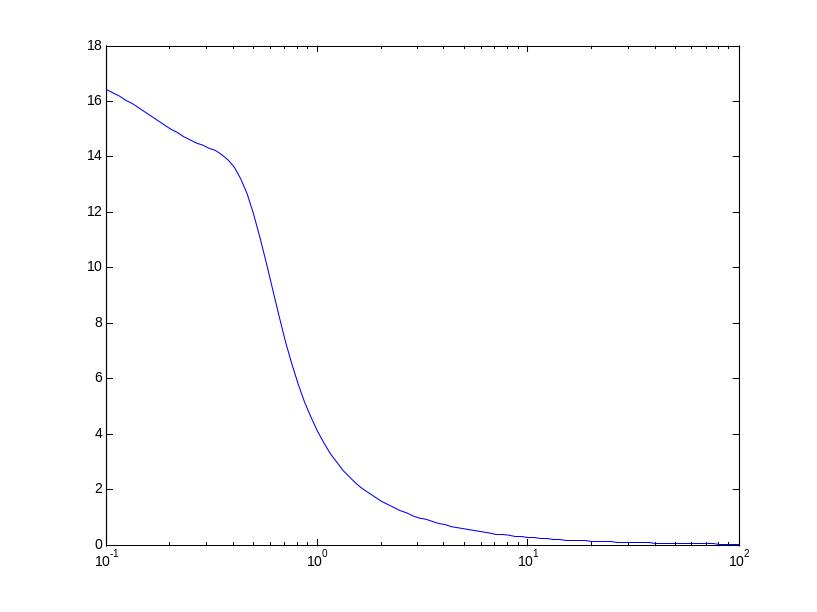
для того, чтобы найти статический коэффициент усиления по АЧХ, надо посмотреть значение АЧХ при
.для того, чтобы найти полосу пропускания по АЧХ, надо посмотреть при каком значении частоты коэффициент усиления равен 0,707.
реакция на сигнал, состоящий из прямоугольных импульсов
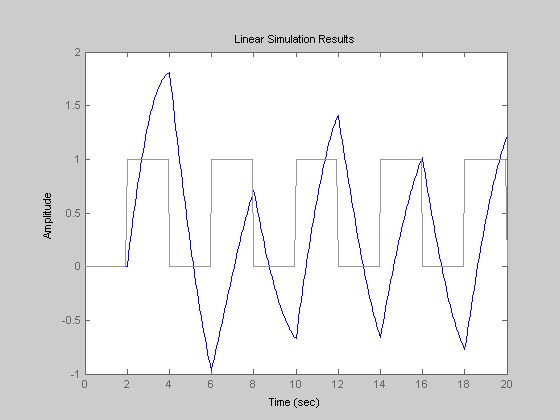
Вывод: в данной лабораторной работе освоили методы анализа одномерной линейной непрерывной системы с помощью среды MATLAB. Научились водить модель системы в виде передаточной функции, строить эквивалентные модели в пространстве состояний в форме «нули полюса», определять коэффициент усиления в установившемся режиме и полосу пропускания системы, строить импульсную и переходную характеристику, карту расположения нулей и полюсов, частотную характеристику, использовать окно LTIViewer для построения различных характеристик , и строить процессы на выходе линейной системы при произвольном входном сигнале.