155 Г лава 12. Колебания

Глава 12. Колебания

12.1. Гармонические колебания физической величины.

Пусть физическая величина зависит от времени по гармоническому закону:

, (12.1)

где , , , - постоянные, причем и положительны. Говорят, что величина совершает гармонические колебания вокруг среднего значения . Коэффициент называется амплитудой колебаний, называется циклической частотой. Величину , являющуюся аргументом функции "косинус", называют фазой колебаний, а её значение в момент времени называют начальной фазой. Разность называется отклонением величины от среднего значения. Отклонение зависит от времени по закону:

. (12.2)

Таким образом, величина совершает гармонические колебания вокруг нулевого значения. Далее мы будем иметь дело в основном с отклонением гармонически колеблющейся величины от ее среднего значения.

Учитывая, что , находим из (12.2), что величина меняется в пределах от до , причем зависимость является периодической с периодом ,

. (12.3)

Графически зависимость (12.2) изображается синусоидой, рис. 12.1.

Рис. 12.1.

Частотой колебаний называется число периодов в единице времени:

. (12.4)

Пример. 12.1. Величина зависит от времени по закону:

, (12.5)

где , , - постоянные, , . Её можно представить в виде (12.1), если положить .

Для первой и второй производных функций (12.2) имеем:

, (12.6)

. (12.7)

Из (12.7) находим:

, (12.8)

Дифференциальное уравнение 2-го порядка вида (12.8) называется уравнением гармонических колебаний. Таким образом, мы показали, что гармоническая функция времени вида (12.2) удовлетворяет уравнению гармонических колебаний. В теории дифференциальных уравнений доказывается, что справедливо и обратное утверждение: если некоторая функция удовлетворяет уравнению гармонических колебаний, то она зависит от времени по гармоническому закону (12.2).

Системы, в которых совершаются гармонические колебания каких-либо физических величин, характеризующих эти системы, в физике принято называть гармоническими осцилляторами.

Пример 12.2. Найдем решение уравнения (12.8), удовлетворяющее начальным условиям: , . Поскольку решение имеет вид (12.2), то, полагая , , получим:

. (12.9)

Полагая в (12.6) , , имеем:

. (12.10).

Из (12.9), (12.10) находим:

. (12.11)

Итак, решение уравнения гармонических колебаний, удовлетворяющее заданным начальным условиям, имеет вид (12.2), причем величины и определяются формулами (12.11).

12.2. Кинематика и динамика одномерных гармонических колебаний материальной точки

Рассмотрим одномерное, то есть совершаемое вдоль некоторой прямой, которую примем за ось , гармоническое колебательное движение частицы массы . Если выбрать начало отсчета по оси в той точке, вокруг которой происходят колебания, то отклонение материальной точки будет совпадать с её координатой по оси и зависимость определяется формулой (12.2). Согласно (12.6), (12.7), проекции скорости и ускорения частицы на ось равны:

, (12.12)

. (12.13)

Найдем проекцию на ось силы, действующей на гармонически колеблющуюся частицу вдоль этой оси. Из (12.13) и второго закона Ньютона находим: ,

. (12.14)

Итак, действующая на гармонически колеблющуюся частицу сила пропорциональна отклонению и направлена в противоположную отклонению сторону. Справедливо и обратное утверждение: если действующая на частицу сила пропорциональна отклонению и направлена в противоположную отклонению сторону, то частица совершает гармонические колебания. Действительно, если , где - положительная постоянная, то, учитывая, что , получим:

. (12.15)

Решение уравнения (12.15), являющегося уравнением гармонических колебаний, имеет вид (12.2), причем

. (12.16)

Таким образом, частица, на которую действует сила , где - положительная постоянная, совершает гармонические колебания с циклической частотой, определяемой формулой (12.16).

При перемещении частицы из положения с координатой в положение с координатой результирующая сила совершает работу

,

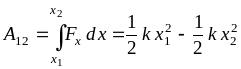которая определяется начальным и конечным положениями частицы. Поэтому частице можно приписать потенциальную энергию . Учитывая, что , получим:

. (12.17)

Таким образом, полная механическая энергия частицы равна:

. (12.18)

Подставляя (12.2) и (12.12) в (12.18) и учитывая (12.16), получим, что . Таким образом, механическая энергия частицы, совершающей одномерные гармонические колебания, сохраняется.

Пример 12.3. Грузик массы подвешен на невесомой пружине с коэффициентом жесткости . Вычислим циклическую частоту колебательного движения грузика вдоль вертикального направления. Положению равновесия грузика припишем координату вдоль вертикальной оси (пружина в этом положении растянута, сила её натяжения компенсирует силу тяжести, действующую на грузик. При отклонении грузика от положения равновесия на него будет действовать результирующая сила , где - координата грузика вдоль оси . Эта сила стремится вернуть грузик к положению равновесия. Заключаем, что грузик будет совершать гармонические колебания с циклической частотой, определяемой формулой (12.16). С такой же частотой грузик колебался бы на пружине и в том случае, если бы каким-либо образом произошло "отключение" силы тяжести, однако эти колебания происходили бы вблизи другого, более высоко расположенного положения равновесия, соответствующего нерастянутой пружине. Потенциальная энергия грузика определяется формулой (12.17).

Рис. 12.2.

Задача 12.1. Определить циклическую частоту колебаний бруска массы в системе, изображенной на рис. 12.2. Коэффициенты жесткости пружинок равны и . Трение отсутствует. Считать, что положению равновесия бруска соответствуют недеформируемые пружины. Указание. Брусок совершает поступательное движение. Поэтому к нему применимы результаты, полученные выше для материальной точки.

Ответ: .