Розділ 3 Система як математичний об'єкт

Поняття системи використовувалося протягом всієї історії цивілізації, однак аж до середини двадцятого століття воно не було предметом особливої наукової уваги. Цікавість до нього різко зросла після того, як воно узвичаїлося у менеджерів і пов'язаних з ними політиків, економістів і військових. Зокрема, у їх середовищі з'явився термін "системний аналіз". Це відбулося, у першу чергу, внаслідок усвідомлення того, що в будь-якій сфері людської практики між подіями в сьогоденні і подіями в досить віддаленому майбутньому може бути зв'язок, який не можна ігнорувати. Як бачимо, у поняття системи вкладалося поняття зв'язку.

Хоча поняття системи має виняткову узагальненість: усе є системою - воно не є первинним, тобто простим, і потрібні інші поняття для його визначення. З'ясуємо, що це за поняття.

Насамперед це поняття зв'язку, тому що поняття системи є похідним від нього. Але зв'язок здійснюється тільки через взаємодію, що означає залежність значень, застосованих одним процесом у сучасний момент часу t, від того, яких значень набув інший процес. Тому ще потрібні поняття часу і процесів у часі. Множину моментів часу будемо позначати через Т.

Коротко можна сказати: будь-яка система реального світу - це процеси, які взаємодіють у часі. Однак такого розуміння ще недостатньо для пояснення того, чому в результаті взаємодії процеси набувають тих чи інших значень.

Залежність значень одного з процесів від того, яких значень набуває інший, свідчить про наявність особливого відношення між ними, що має назву причинно-наслідкового. Процес, значення якого залежать від значень, набутих іншим процесом, називається процесом-наслідком, а інший - причиною. У теорії систем причинний процес називають входом (input), а процес-наслідок називають виходом (output).

Множину значень входу будемо позначати через U, значень виходу - через Y, а елементи цих множин - через u і у, відповідно.

Однак для визначення процесу взаємодії цих понять недостатньо. Вище в основу поняття взаємодії покладена наявність залежності виходу від входу. Разом з тим при логічному аналізі характеру цієї залежності виявляється, що безпосереднього зв'язку між ними немає.

Дійсно, реальна подія в момент часу t не може залежати від того, чого в цей момент не існує. Події, що реалізувалися в процесі-вході раніше, тобто в моменти, що передують моментові t, у цей момент t не є реальністю. Подія, що являє собою конкретне значення виходу в момент t, не залежить від значень входу в моменти τ< t. Разом з тим вихід у момент t також не залежить від входу, що реалізується в той самий момент t, тому що вплив однієї події на іншу не може бути миттєвим, поширення сигналу завжди відбувається зі скінченною швидкістю, причина і наслідок не можуть виникнути одночасно (інакше не зрозуміло, що назвати причиною і що - наслідком). Вхід у момент t не може забезпечити відповідний йому вихід у цей самий момент t, оскільки в цей момент вихід уже існує.

Таким чином, доходимо до логічного протиріччя: з одного боку, правильним є те, що вихід залежить від входу, але з іншого - також істинно, що не залежить. Розв’язання цього протиріччя полягає в тому, що залежність виходу від входу є опосередкованою. Це означає, що існують певні об'єкти, які пов'язують усі входи-причини до моменту t і вихід у цей момент.

У теорії систем ці об'єкти називаються станами. Помітимо, що стан як первинне поняття не визначається.

Множину станів будемо позначати через X, а його елементи як х.

Отже, у кожен момент t система характеризується деяким станом. Цей стан однозначно визначає значення виходу в цей момент t. У стані накопичуються всі причини, що реалізувалися в минулому і визначають подію в сьогоденні. Тут простежується аналогія стану з пам'яттю, причому в пам'яті системи накопичується вся передісторія впливу середовища на систему.

Далі, оскільки значення виходу в конкретний момент t, як реальна подія в цей момент, породжується станом, що реалізується в цей момент, то в поняттях математичної моделі це означає, що y(t) є визначеною функцією від x(t). Отже, існує відображення g : X—>У і при цьому y(t) = g(x(t)). У загальному випадку характер цієї залежності може змінюватися в часі, тобто g також є функцією від t, і тоді

y(t)=g(t,x(t)). (3.1)

У теорії систем g називають відображенням або оператором виходу.

Нарешті, для визначення поняття системи необхідно встановити залежність стану від входу і попередніх станів. У теорії систем встановлюється, що стан у майбутній момент t однозначно визначається значеннями, прийнятими входом, починаючи з поточного моменту τ і до моменту t, за умови, що в момент τ реалізувався визначений стан х(τ).

Для формально-математичного представлення зазначеного зв'язку входів зі станами введемо наступне позначення. Нехай u є відображенням з Т у U. Тоді зазначений зв'язок реальних процесів математично представляється деяким відображенням  з множини T  T  X  U у множину X, а саме:

x(t) = (t;,x(),u),t≥. (3.2)

Рівняння (3.2) описує стан у системі в момент t за умови, що в момент  реалізувалися стан x() і вхід u.

Відображення σ називають перехідним або оператором динаміки станів.

З фундаментальних принципів філософії і природничих наук випливає, що відображення σ повинно задовольняти умови:

1. для будь-яких t, х і и виконується рівність

(t; t, x, u)=x;

2) для будь-яких t₀ ≤ t₁ ≤ t₂, x і u виконується рівність

 (t₂; t₀, x, u) = (t2; t₁,  (t₁; t₀, x, u), u);

3) для будь-яких t, t₀, x, u₁ і u₂, причому u₁() = u₂() при t₀<<t, виконується рівність

(t; t₀, x, u₁)=(t; t₀, x, u₂),

які розглядаються як аксіоми теорії систем.

Перша з них називається аксіомою погодженості, яка означає, що в той самий момент система не може бути в різних станах. Друга зветься аксіомою детермінізму і формалізує ту обставину, що стан системи при заданому вході однозначно визначає майбутні стани системи. Третя називається аксіомою причинності і відбиває незалежність стану в момент t від того, яких значень набуде вхід у моменти часу, більші за t.

У результаті одержуємо наступне визначення системи як математичного поняття. Система визначена, якщо задані множини Т, U, Y, X, оператор виходу g, оператор динаміки станів  і рівняння (3.1) і (3.2).

Рівняння (3.1), (3.2) описують усі потенційно можливі в системі процеси і серед їх розв’язків немає процесів, що в ній не відбуваються. За своїм змістом ці рівняння представляють у математичній формі закон розвитку (поводження, руху) системи. Тому тріаду {X, g, }, що визначає ці рівняння, будемо називати законом. За умови, що відомі початковий стан x(t₀) і вхід и, рівняння (3.1 ) і (3.2 ) дозволяють прогнозувати вихід y(t) для будь-якого t > t₀ за формулою у(t) = g(t,  (t; t₀, x(t₀), u)).

Рисунок 3.1 Рисунок 3.2

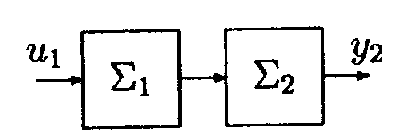
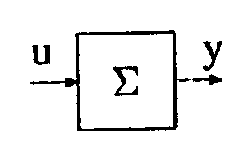
У теорії систем, крім математичного, також використовується схематичне представлення системи, як показано на рис. 3.1. У цьому представленні стрілки ПОказують входи і виходи, а прямокутник - їхній причинно-наслідковий зв'язок, обумовлений законом перетворення входу у вихід.

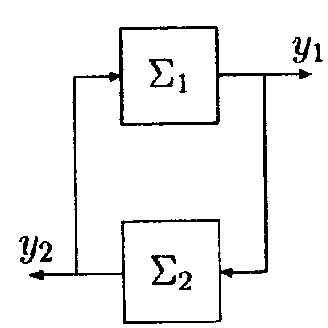
Рисунок 3.3

Можна розглянути дві системи, що взаємодіють між собою. Це означає, що якісь входи однієї із систем одночасно є виходами іншої. З'єднання або композиція цих систем утворюють нову систему. Якщо тільки одна з цих систем має як вхід вихід іншої системи, як показано на рис. 3.2, то таке з'єднання називається послідовним. Якщо ж кожна з цих систем має як вхід вихід іншої системи, як показано на рис.3.3, то це називається з'єднанням зі зворотним зв'язком.

Розглядаючи інші системи Σ_1,..., Σ_m і ототожнюючи входи одних з виходами інших, будемо одержувати різноманітні і складні системи. Зокрема, так одержують системи з ієрархічною будовою причинно-наслідкових зв'язків. Така композиція знову буде системою відповідно до введених визначень: у неї будуть свої входи, свої виходи і свої оператори виходу і динаміки станів.

Наведене поняття системи ввів Р. Калман. Він виділив вихідні поняття, сформулював основні проблеми й одержав перші фундаментальні результати цієї теорії. Вони знайшли широке практичне застосування в багатьох галузях, у тому числі в економіці .

У зв'язку з введеною конструкцією поняття системи важливо відзначити наступне. Наукові поняття є образами об'єктів (процесів) матеріального світу. Це означає, що для кожного поняття існує свій матеріальний прообраз. Це стосується і поняття системи. Однак, якщо поняття входу і виходу мають прообрази в матеріальному світі, то поняття стану такого прообразу не має. Отже, або його прообрази є об'єктами іншого, нематеріального світу, або станів взагалі не існує, тобто вони є фікцією. Але, з одного боку, поняття стану використовують усі природничі науки, а з іншого - без станів, як було показано, не може бути зв'язку подій у матеріальному світі.