2. Условия и уравнения равновесия произвольной системы сил

Из теоремы о приведении системы сил к силе и паре сил можно вывести условия равновесия системы сил, действующих на тело.

Если система сил находится в равновесии, то в равновесии находится и эквивалентная ей система, состоящая из силы и пары сил.

Чтобы такая система сил была эквивалентна нулю, необходимо и достаточно равенства нулю, как силы , так и момента пары , равного главному моменту .

Условия равновесия системы сил в векторной форме

Для равновесия системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы главный вектор системы сил равнялся нулю, и главный момент системы сил относительно любого центра приведения так же равнялась нулю.

Иначе, для того, чтобы ( , , ) ~ 0 , необходимы и достаточны условия:

= 0, = 0

Условия являются векторными условиями равновесия для любой системы сил.

Условия равновесия пространственной системы сил в аналитической форме

Если при равновесии системы сил, приложенных к твердому телу, главный вектор и главный момент системы равны нулю, то их проекции на любую ось системы координат также равны нулю. Поэтому из векторных условий равновесия пространственной системы сил следует шесть условий:

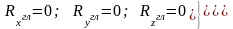
Модули главного вектора и главного момента рассматриваемой системы сил определяются по формулам:

Через силы системы эти шесть уравнений выражаются в форме:

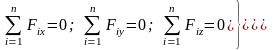
Таким образом, для равновесия произвольной пространственной системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы три суммы проекций всех сил на оси декартовых координат равнялись нулю и три суммы моментов всех сил относительно трех осей координат так же равнялись нулю.

Из векторных условий равновесия плоской системы сил следует три условия:

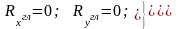
Через силы системы эти уравнения выражаются в форме:

Для равновесия произвольной плоской системы сил, приложенных к твердому телу (Рис. 2), необходимо и достаточно, чтобы суммы проекций всех сил на каждую из двух взаимно перпендикулярных осей координат, лежащих в плоскости действия сил, равнялись нулю и сумма алгебраических моментов этих сил относительно любой точки, лежащей в плоскости действия сил, также равнялась нулю.

Рис. 2

Как показано, любая система сил приводится в общем случае к силе, равной главному вектору и приложенной в произвольном центре О , и к паре с моментом, равным главному моменту . Найдем, к какому простейшему виду может приводиться пространственная система сил, не находящаяся в равновесии. Результат зависит от значений, которые у этой системы имеют величины и .

1. Если при приведении данной системы сил к какому-либо центру окажется, что главный вектор ≠ 0, а главный момент = 0, то такая произвольная система сил приводится к одной силе , равнодействующей системе сил. Равнодействующая сила в этом случае проходит через центр приведения, а по величине и направлению совпадают с главным вектором .

2. Если для данной системы сил ≠ 0, ≠ 0, но , то эта система также приводится к равнодействующей, равной , но не проходящей через центр приведения О.

3. Если при приведении системы сил к какому-либо центру окажется, что главный вектор = 0, а главный момент ≠ 0, то она приводится к паре сил. В этом случае, значение главного момента от выбора центра приведения не зависит.

4. Если при приведении системы сил к центру окажется, что = 0 и = 0, то система будет находиться в равновесии.

Если = 0, то силы , , , приведенные к центру О , взаимно уравновешиваются.

Если =0, то присоединенные пары взаимно уравновешиваются.

Следовательно, данная система сил взаимно уравновешивается.

Для случая, когда любая система сил, приложенных к твердому телу, приводится к равнодействующей силе, часто применяют теоремы Вариньона.

Теорема. Если данная система сил имеет равнодействующую, то векторный момент равнодействующей относительно любого центра О равен векторной сумме моментов всех сил системы относительно того же центра: