Тема 2. Произвольная система сил лекция № 4 произвольная система сил

1. Приведение сил к заданному центру

2. Условия и уравнения равновесия системы сил

3. Равновесие с учетом сил трения

Литература: Парфенов Ю.М., Теплов Г.Д., Цыглин В.А. Механика, ч.1, СПБВМИ, 2006,

стр. 48 – 70.

1. Приведение силы к заданному центру

Равнодействующая системы сходящихся сил непосредственно находится с помощью закона параллелограмма сил. Аналогичную задачу можно будет решить и для произвольной системы сил, если найти для них метод, позволяющий перенести все силы в одну точку. Такой метод дает следующая теорема: силу, приложенную к твердому телу, можно переносить параллельно самой себе в любую точку тела, добавляя при этом пару сил, векторный момент которой равен векторному моменту переносимой силы относительно новой точки приложения силы.

Пусть дана сила , приложенная к твердому телу в точке А (Рис.1). Известно, что силу, приложенную к твердому телу, можно переносить вдоль ее линии действия, от чего действие силы на твердое тело не изменяется.

Рис.1

Теперь докажем, что силу можно переносить на другую, параллельную линию действия. Но этот перенос следует компенсировать добавлением соответствующей пары сил. Приложим в точке О тела, выбранной за центр приведения, систему двух равных по величине, но противоположных по направлению сил и , параллельных заданной силе . Система сил и составляет систему сил, эквивалентную нулю, и ее можно добавить к любой заданной системе сил.

Пусть по величине 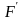= = F

Тогда ( ) ( , , ) [ , ( , )]

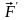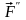Система двух равных по величине и противоположных по направлению параллельных сил ( , ) составляют пару сил, которую называют присоединенной парой сил.

Итак, вместо силы , приложенной в точке А, получена сила , равная ей по величине и направлению, но приложенная в точке О, и присоединенная пара сил ( , ).

Опустив из точки О перпендикуляр на линию действия силы , получим плечо этой пары сил h и найдем модуль ее момента

M = Fh = M₀ ( ),

равный модулю момента силы относительно центра приведения (т.О).

Направление вектора момента присоединенной пары сил совпадает с направлением вектора ₀ ( ) момента силы относительно центра приведения.

Так как эти векторы равны по модулю и совпадают по направлению, то они геометрически равны, то есть,

= ₀ ( ) =

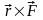
Процесс замены силой и парой сил ( , ) называют приведением силы к заданному центру О.

Этот метод был предложен французским ученым Пуансо (1777-1859).

Рассмотрим частные случаи приведения силы к заданному центру.

Приведение произвольной системы сил к силе и паре сил.

Решим теперь задачу о приведении произвольной системы сил к данному центру, то есть, о замене данной системы сил другой, ей эквивалентной, но значительно более простой, а именно состоящей только из одной силы и пары сил.

Докажем для этого основную теорему статики (теорему Пуансо): любую произвольную систему сил, действующую на твердое тело, можно в общем случае привести к силе и паре сил.

Такой процесс замены системы сил одной силой и парой сил называют приведением системы сил к заданному центру:

Пусть дана произвольная система сил ( , ,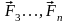 ), приложенных к твердому телу. Выберем произвольную точку О тела за центр приведения и каждую силу заданной системы сил приведем к точке О присоединяя при этом соответствующие пары сил.

Получим: ( , , .

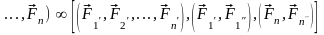Таким образом, система из n сил заменена системой из 3n сил, то есть, в точке О приложена система сходящихся сил (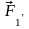 , , 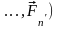и на тело действует так же система n присоединенных пар сил: .

Векторные моменты присоединенных пар сил), можно выразить через векторные моменты заданных сил:

Систему сходящихся сил 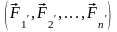заменяем одной силой , их равнодействующей, которая равна векторной сумме сил 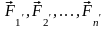и геометрически изображается замыкающим вектором силового многоугольника, построенного на этих силах (Рис.3.11).

Итак ∞

где =

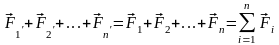
Для системы сходящихся сил сила является равнодействующей силой, а для заданной системы сил ( , ,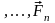 ), сила является лишь только ее векторной суммой, или главным вектором.

Главным вектором системы сил называют вектор, равный векторной сумме этих сил и обозначают . Эта сумма изображается вектором, замыкающим силовой многоугольник, построенный на силах, то есть

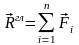
Систему присоединенных пар сил по теореме о сложении пар сил можно заменить одной парой сил с векторным моментом 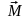= , который называют главным моментом системы сил относительно центра О. Главный момент равен векторной сумме моментов присоединенных пар. Учитывая формулу (3.11), для имеем

Итак, главным моментом системы сил относительно точки О тела называют сумму векторных моментов всех сил системы относительно этой точки.

Главный момент системы является вектором, замыкающим векторный многоугольник, образованный при сложении векторных моментов сил системы относительно выбранного центра.

Таким образом, любая система сил, действующих на абсолютно твердое тело, при приведении к произвольно выбранному центру О заменяется одной силой , равной главному вектору системы сил и приложенной в центре приведения О, и одной парой сил с моментом , равным главному моменту системы сил относительно центра о.

Следует заметить, что: 1) не является здесь равнодействующей данной системы сил, так как заменяет систему сил не один, а в совокупности с парой сил. 2) значение от выбора центра О не зависит, а значение же зависит, так как при изменении положения центра О может в общем случае изменяться вследствие изменения значений моментов отдельных сил. Поэтому всегда необходимо указывать, относительно какого центра определяется главный момент.

Следовательно, при приведении произвольной системы сил к различным центрам приведения некоторые величины, характеризующие систему сил, остаются неизменными, другие изменяются.

Приведение плоской системы сил к заданному центру

Плоской системой сил, приложенных к твердому телу, называют такую систему сил, линии действия которых лежат в одной плоскости.

Основная теорема статики справедлива для любой системы сил, в том числе, и для плоской системы сил.

Для плоской системы главный вектор лежит в плоскости действия сил, если за центр приведения выбрать точку в плоскости действия сил.

Все присоединенные пары сил тоже лежат в этой плоскости, а векторные моменты этих пар перпендикулярны к ней и взаимно параллельны.

Главный момент ,характеризующий векторный момент пары сил, эквивалентный присоединенным парам, перпендикулярен к главному вектору. Он является векторной суммой параллельных векторов.

В этом случае главный момент по величине равен сумме алгебраических моментов сил относительно центра приведения.

Для плоской системы сил вместо векторного главного момента используют понятие алгебраического главного момента.

Алгебраическим главным моментом плоской системы сил относительно центра приведения, лежащего в плоскости действия сил, называют сумму алгебраических моментов этих сил относительно центра приведения.