3.Сложение и условие равновесия пар сил

Теорема о сумме моментов сил пары.

Сумма векторных моментов сил, входящих в состав пары, относительно любой точки не зависит от вектора точки и равна векторному моменту этой пары сил, то есть, для пары сил ( , )

где О - любая точка

Эта теорема имеет важное значение при решении задач, когда надо вычислять сумму моментов сил пары относительно какой-либо точки. Для этого достаточно взять момент пары сил, что справедливо для любой точки.

Свойства пар сил.

Векторный момент эквивалентной пары сил равен сумме векторных моментов заданных пар (Рис. 11).

Рис. 11

Таким образом, чтобы сложить две пары сил, лежащих в пересекающихся плоскостях, надо сложить их векторные моменты по правилу параллелограмма в какой-либо точке тела. Сложение пар сил, лежащих в одной плоскости или параллельных плоскостях, есть частный случай сложения пар сил в пересекающихся плоскостях, так как в этом случае их векторные моменты параллельны и, следовательно, векторное сложение перейдет в алгебраическое.

Последовательно, применяя правило параллелограмма к каждым двум векторным моментам пар сил, можно любое количество пар сил в общем случае заменить одной парой сил, векторный момент которой равен сумме векторных моментов заданных пар сил:

=

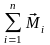
Если это сложение выполнять графически, особенно когда векторные моменты пар сил находятся в одной плоскости, то получается, что векторный момент эквивалентной пары сил изображается замыкающей векторного многоугольника, построенного из векторных моментов заданных пар сил.

Для пар сил, расположенных в одной плоскости, теорема об их сложении формулируется так: пары сил, действующие на твердое тело и расположенные водной плоскости, можно привести к одной паре сил, алгебраический момент которой равен сумме алгебраических моментов составляющих пар сил, то есть,

Условия равновесия пар сил.

Если пары сил, действуя на твердое тело, взаимно уравновешиваются, то момент равнодействующей пары сил равен нулю, то есть

– условие равновесия пар сил

Пары сил взаимно уравновешиваются, если векторная сумма их моментов равна нулю.

Если пары сил расположены в параллельных плоскостях, то векторы их моментов складываются алгебраически,

Пару сил можно уравновесить только парой сил.

4. Момент силы относительно оси

Положим, что к твердому телу в некоторой точке приложена сила .

Чтобы вычислить момент этой силы относительно оси z, следует спроецировать силу на плоскость , перпендикулярную к оси z, а затем вычислить момент ее проекции на эту плоскость относительно точки О пересечения оси z с плоскостью , приписав этому моменту знак плюс или минус (Рис.12).

Рис. 12

Таким образом, моментом силы относительно оси oz называется взятое со знаком плюс или минус произведение модуля проекции силы на плоскость, перпендикулярную к оси, на ее плечо h₁ относительно точки пересечения оси с плоскостью:

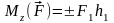
где - проекция силы на плоскость , перпендикулярную к оси oz;

h₁ - плечо силы

Момент силы относительно оси считается положительным, если, смотря навстречу оси z, можно видеть проекцию стремящейся вращать плоскость  вокруг оси oz в сторону, противоположную вращению часовой стрелки.

Момент силы относительно оси изображается отрезком, отложенным по оси oz от точки О в положительном направлении, если 0 и в отрицательном , - если  0.

Значение момента силы относительно оси может быть также выражено удвоенной площадью треугольника

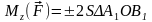
Момент силы относительно оси равен нулю в двух случаях:

1) если = 0, то есть, линия действия силы параллельна оси oz.;

2) если h₁, то есть, линия действия силы пересекает ось oz..

Таким образом, если сила и ось лежат в одной плоскости, то момент силы относительно этой оси равен нулю.

Из определения момента силы относительно оси следует, что введенный выше алгебраический момент силы относительно точки можно считать моментом силы относительно оси, проходящей через эту точку, перпендикулярно к плоскости, в которой лежит сила и моментная точка.

Ранее установлено, что ,

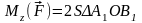
Так как треугольник является проекцией треугольника АОВ на плоскость , перпендикулярную к оси оz, то его площадь равна площади треугольника АОВ, умноженной на косинус угла между этими плоскостями.

Из геометрии известно, что угол между плоскостями  и  равен углу между перпендикулярами к этим плоскостям. Поэтому угол между плоскостью треугольника АОВ и плоскостью  равен углу между перпендикулярами к этим плоскостям, то есть, углу между моментом 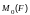и осью oz . Из этого следует, что

=

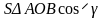где угол  - двугранный угол между плоскостями треугольников АОВ и А₁ОВ₁

Умножив обе части этого равенства на два, получим

=

следовательно, =

или = `

Проекция момента силы относительно точки на ось, проходящую через эту точку, равна моменту силы относительно этой оси.

Если сила расположена в плоскости, перпендикулярной к оси, то

=  1, и =

Аналитические выражения моментов силы относительно координатных осей.

Возьмем прямоугольную систему координат oxyz, орты осей которой .

силы относительно начала координат, как известно из § 2.1, выражается формулой = где - радиус-вектор точки приложения силы относительно начала координат (рис.13).

Разложим вектор на составляющие по осям координат:

=

где - проекции на оси координат.

Рис.13

Из векторной алгебры известно, что векторное произведение можно представить определителем:

= ,

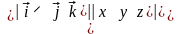где x, y, z - проекции вектора на оси координат

- проекции вектора на оси координат

Приравнивая значения и определителя, разложенного по элементам первой строки, получаем

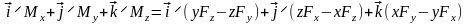
сопоставляя левые и правые части последнего равенства, находим проекции момента на оси координат, равные, моментам силы относительно этих осей.

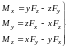
- аналитические выражения момента силы относительно координатных осей

Величину векторного момента M₀(F) и косинусы углов его с осями координат определяем по формулам: