Лекция № 3 пара сил и момент силы относительно точки и оси

1. Момент силы относительно точки

2. Пара сил и ее момент

3. Сложение и условия равновесия пар сил

4. Момент силы относительно оси

Литература: Парфенов Ю.М., Теплов Г.Д., Цыглин В.А. Механика, ч.1, СПБВМИ, 2006,

стр. 15 – 37.

1.Момент силы относительно точки

Мера механического воздействия, учитывающая положение силы по отношению к данной точке или оси, характеризуется особой механической величиной, называемой моментом силы относительно точки или относительно оси.

Точку, относительно которой берется момент, называют центром момента, а момент силы относительно этой точки - моментом относительно центра.

Если под действием приложенной силы тело может совершать вращение вокруг некоторой точки, то момент силы относительно этой точки будет характеризовать вращательный эффект силы.

При рассмотрении пространственной системы сил, приложенных к твердому телу, применяется понятие векторного момента силы относительно точки.

Моментом силы относительно точки О называется вектор (Рис. 10), равный векторному произведению радиуса-вектора 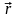точки приложения силы относительно точки О на вектор силы.

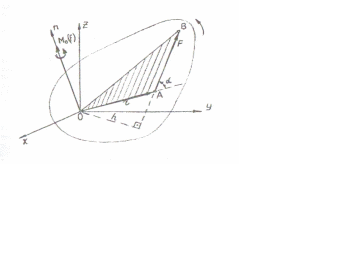
Рис. 10

Из определения векторного произведения следует, что вектор приложен в точке О (центре момента), направлен перпендикулярно плоскости, содержащей векторы , и точку О ,в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра против хода часовой стрелки.

Модуль векторного произведения равен

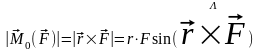
где - плечо силы относительно точки О, то есть, кратчайшее расстояние от точки до линии действия силы .

Подставив h из выражения (б) в выражение (а), получим

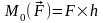
Из полученного выражения следует, что модуль момента силы относительно точки (центра момента) равен произведению модуля силы на ее плечо относительно этой точки.

Таким образом, данный вектор полностью определяет вращательный эффект приложенной к телу силы относительно точки О (центра приведения); его линия действия определяет плоскость вращения; его направление - направление вращения; его модуль - интенсивность вращательного воздействия.

Размерность момента силы в CИ [Hм]. Вектор момента силы относительно точки есть вектор закрепленный, приложенный в центре момента .

В случае, когда силы, действующие на тело, лежат в одной плоскости, вместо векторного момента силы относительно точки используют алгебраический момент.

Численно алгебраический момент относительно точки О равен удвоенной площади треугольника, построенного на силе (АВ ) и моментной точке

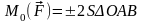
Знак «+» -вращение против хода часовой стрелки;

Знак «-» - вращение по ходу часовой стрелки;

- площадь треугольника.

Момент силы 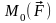- равен нулю, если плечо h равно нулю, то есть, когда линия действия силы проходит через моментную точку; - не изменяется при переносе точки приложения силы вдоль ее линии действия.

2. Пара сил и ее момент. Сложение и условие равновесия пар сил

Совокупность двух равных по модулю, параллельных и направленных в противоположные стороны сил называется парой сил. Пара сил является особой мерой механического воздействия на тело. При действии на твердое тело она стремится сообщить ему вращательное движение.

Таким образом, силы, составляющие пару, не находятся в равновесии, не имеют равнодействующей и не могут быть заменены одной силой.

Действие пары сил на твердое тело сводится к некоторому вращательному эффекту, который характеризуется величиной, называемой моментом пары сил.

Момент пары определяется:

- модулем момента пары, равным произведению модуля сил пары на ее плечо;

- положением в пространстве плоскости действия пары;

- направлением поворота пары в плоскости ее действия.

Таким образом, как и момент силы относительно центра, момент пары величина векторная.

Введем следующее определение: моментом пары сил называется вектор 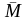, равный по модулю произведению модуля сил пары на ее плечо и направленный перпендикулярно плоскости действия пары в ту сторону, откуда поворот тела под действием пары наблюдается против хода часовой стрелки.

Согласно этому определению модуль момента пары равен:

,

где плечо пары

Сформулируем условия эквивалентности двух пар сил, используя наиболее общую характеристику пары сил - ее векторный момент.

Известно, что пару сил можно как угодно поворачивать в плоскости ее действия; от этого действие пары сил на твердое тело не изменяется, если алгебраический момент пары сил остается таким же. Следовательно, векторный момент пары сил можно переносить параллельно самому себе в любую точку твердого тела, лежащую в плоскости действия пары сил.

У пары сил можно изменять плечо и силы, сохраняя при этом алгебраический момент пары и плоскость действия.

Пару cил, не изменяя ее действия на твердое тело, можно переносить из одной плоскости в другую, параллельную ей. Поэтому векторный момент пары сил можно переносить параллельно самому себе в любую точку тела, не изменяя действия пары сил на твердое тело.

Из этого следует, что векторный момент пары сил, действующей на твердое тело, есть свободный вектор, т.е. он характеризуется только величиной и направлением, а точкой приложения у него может быть любая точка тела и, следовательно, векторный момент пары сил не обязательно прикладывать посредине отрезка, соединяющего точки приложения сил пары.

Таким образом, две пары сил, действующие на одно и то же твердое тело, эквивалентны, если они имеют одинаковые по величине и направлению векторные моменты.