2. Условия и уравнения равновесия системы сходящихся сил
Система сил, линии действия которых пересекаются в одной точке, называется сходящейся (Рис. 8):
Рис. 8
Для равновесия системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы равнодействующая, а, следовательно, и главный вектор этих сил были равны нулю. Условия, которым при этом должны удовлетворять сами силы, можно выразить в геометрической и или в аналитической форме.
Геометрическое условие равновесия
Так как главный вектор системы сил определяется как замыкающая сторона силового многоугольника, построенного из этих сил, то может обратиться в нуль только тогда, когда конец последней силы в многоугольнике совпадает с началом первой силы, то есть, когда многоугольник замыкается.
Следовательно, для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнутым.
Аналитические условия равновесия.
Аналитически модуль главного вектора системы сил определяется формулой
Так
как под корнем стоит сумма положительных
слагаемых, то
обратится в нуль только тогда, когда
одновременно
,
то есть, как следует из формул, когда
действующие на тело силы будут
удовлетворять равенствам:
;
;
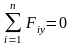Последние равенства выражают условия равновесия в аналитической форме для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из трех координатных осей были равны нулю.
Если все действующие на тело сходящиеся силы лежат в одной плоскости, то они образуют плоскую систему сходящихся сил (частный случай произвольной системы сил). В случае плоской системы сходящихся сил получим, очевидно, только условия равновесия:
;
3. Теорема о равновесии трех непараллельных сил
При решении задач статики иногда удобно пользоваться следующей теоремой: «Если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке».
Пусть к твердому телу в трех точках приложены три непараллельные взаимно уравновешивающиеся силы , , , лежащие в одной плоскости (Рис. 9). Перенесем силы и в точку пересечения линий их действия (точка А) и найдем равнодействующую , которая будет приложена в этой же точке.
Рис. 9
Сила приложена в точке В, будучи уравновешивающей системы сил и , равна по модулю их равнодействующей и направлена по линии ее действия в противоположную сторону
= -
Следовательно, линия действия силы проходит через точку пересечения двух первых сил (точка А), что и требовалось доказать.
Кроме того, три свободных вектора сил , и должны образовать замкнутый треугольник, то есть
+ + = 0
Таким образом, три непараллельные силы могут находиться в состоянии равновесия только тогда, когда они лежат в одной плоскости, пересекаются в одной точке и их свободные векторы образуют замкнутый треугольник. (Необходимое и достаточное условие).