Лекция № 2 система сходящихся сил

1. Способы сложения сил

2. Условия и уравнения равновесия системы сходящихся сил

3. Теорема о равновесии трех непараллельных сил

Литература: Парфенов Ю.М., Теплов Г.Д., Цыглин В.А. Механика, ч.1, СПБВМИ, 2006,

стр. 15 – 37.

1. Способы сложения сил

Решение многих задач механики связано с известной из векторной алгебры операцией сложения векторов и, в частности, сил. Величину, равную геометрической сумме сил какой-нибудь системы, называют главным вектором этой системы сил. Понятие о геометрической сумме мил не следует смешивать с понятием о равнодействующей; для многих систем сил равнодействующей вообще не существует, геометрическую же сумму (главный вектор) можно вычислить для любой системы сил.

Например, две силы, приложенные к телу в одной точке (пересекающиеся в одной точке), имеют равнодействующую, приложенную в той же точке и изображаемую диагональю параллелограмма, построенного на этих силах, как на сторонах (рис.6):

Рис. 6

Если две силы, действующие на тело, приложены в разных точках, то они не имеют равнодействующей. Поясним это примером. Пусть две силы 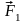и приложены к телу в точках А и В. Сила равна геометрической сумме сил и (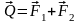 ), как диагональ соответствующего параллелограмма. Но сила не является равнодействующей этих сил, так как одна сила не может заменить действие сил и на данное тело, где бы она ни была приложена.

Если к телу приложены две силы, линии действия которых пересекаются в одной точке, то, как указывалось в аксиоме параллелограмма сил, их равнодействующая приложена в точке пересечения линий действия сил, она изображается диагональю параллелограмма, построенного на этих силах.

Построение параллелограмма сил можно заменить построением треугольника сил изображающего одну из половин этого параллелограмма.

Сложение трех сил, не лежащих в одной плоскости, производится последовательным применением правила параллелограмма. Геометрическая сумма трех сил , и 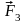в этом случае, изображается диагональю параллелепипеда, построенного на этих силах (правило параллелепипеда), (Рис. 7):

Рис. 7

Если к телу приложена система сил ( , ,…,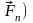 , расположенных в пространстве и линии действия их пересекаются в одной точке, то геометрическая сумма этой системы сил определяется: или последовательным сложением сил системы по правилу параллелограмма, или построением силового многоугольника. Второй способ является более простым и удобным.

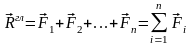
Главный вектор 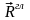системы сходящихся сил геометрически равен равнодействующей этой системы сил . Следовательно, система сходящихся сил , , ,…, имеет равнодействующую , равную их главному вектору и приложенную в точке пересечения сил (или в любой другой точке, лежащей на линии действия силы), то есть:

( , , ,…, ) ;

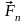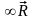Аналитический способ определения величины равнодействующей системы сходящихся сил осуществляется с помощью следующей теоремы геометрии: проекция вектора суммы на какую-нибудь ось равна алгебраической сумме проекций слагаемых векторов на ту же ось. Согласно этой теореме, если есть сумма сил , , ,…, , то есть ,

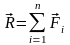то ; ;

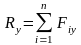Зная ; ; 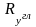, можно определить модуль главного вектора по формуле

Для определения направления вектора воспользуемся обычными выражениями для направляющих косинусов:

; ; .

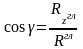где α – угол наклона к оси x; β - угол наклона к оси y; γ - угол наклона к оси z.

Эти уравнения полностью определяют равнодействующую (главный вектор) любой системы сходящихся сил в пространстве.

Если силы заданы их модулями и углами с осями, то для применения аналитического метода сложения надо предварительно вычислить проекции этих сил на координатные оси.