4.Кинетическая энергия системы

В механической системе действуют внешние р^е и внутренние силы рⁱ, которые влияют на движение отдельных масс относительно друг друга (рис. 15). Количество движения не зависело от действия внутренних сил. Наиболее полной характеристикой движения системы может служить кинетическая энергия, т.к. она учитывает изменение модулей (а не векторов) скоростей и, следовательно, влияние всех сил, действующих в системе.

Рис. 15

Кинетическая энергия системы определяется суммой кинетических энергий отдельных входящих в нее масс:

.

Запишем это выражение для отдельной k-ой точки системы с учетом действия на нее внешних и внутренних сил:

.

Суммируя по всем точкам системы, получим:

.

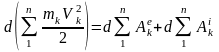Тогда будем иметь:

.

Дифференциал кинетической энергии системы равен сумме элементарных работ внешних и внутренних сил. Интегрируя за конечный промежуток времени в промежутках, соответствующих значениям переменных в точках 1 и 2, найдем:

.

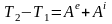Изменение кинетической энергии системы на конечном перемещении равно сумме работ внешних и внутренних сил системы на том же перемещении.

Кинетическая энергия твердого тела.

Твердое тело представляет собой систему материальных точек с постоянными расстояниями между ними. Поэтому при движении твердого тела не возникает взаимного смещения составляющих его масс и работа внутренних сил взаимодействия обращается в нуль.

Тогда: .

Рассмотрим частные случаи движения твердого тела.

а) Поступательное движение.

При поступательном движении все точки твердого тела имеют скорости, равные скорости центра масс (рис. 16).

Рис. 16

.

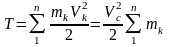Учитывая, что 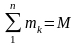- масса всей системы, будем иметь:

.

Кинетическая энергия твердого тела, движущегося поступательно, равна половине произведения массы тела на квадрат скорости центра масс.

б) Вращательное движение.

При вращательном движении все точки тела движутся по концентрическим окружностям относительно оси вращения.

Рис.17

Рассмотрим произвольную точку массой m_k на расстоянии h_k от оси вращения (рис. 17). Линейная скорость этой точки равна 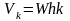, где W – угловая скорость вращения тела.

,

т.к. 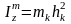- момент инерции массы, следовательно:

.

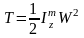Кинетическая энергия тела, вращающегося относительно оси, равна половине произведения его момента инерции относительно оси вращения на квадрат угловой скорости.

в) Плоское движение.

Как известно из кинематики, плоское движение можно представить в виде только поворотов тела вокруг мгновенных центров скоростей. Рассмотрим твердое тело массы m (Рис. 18).

Рис. 18

Мгновенный центр скорости Р располагается от центра масс С на расстоянии 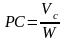, где - линейная скорость центра масс. Тогда можно записать:

.

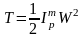Однако положение мгновенного центра скоростей при движении тела все время меняется, поэтому величина 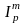будет переменной во времени.

Введем вместо , постоянный момент инерции 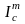, относительно оси, проходящей через центр масс тела. Как известно, его можно представить по формуле перехода в виде:

.

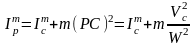Подставляя полученное выражение в формулу для кинетической энергии, получаем:

.

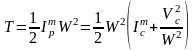После раскрытия скобок будем иметь:

.

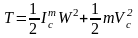Кинетическая энергия тела при плоском движении равна сумме кинетических энергий его вращательного движения вокруг центра масс и поступательного движения вместе с центром масс.