2. Частичные случаи вычисления работы.

а) Работа силы тяжести.

Рассмотрим массу m, движущуюся по траектории 1-2 только под действием силы тяжести (рис. 11).

Рис.11

P_x=0, P_y=0, P_z=-mg.

Тогда:

.

1) Работа силы тяжести не зависит от формы траектории, h=z₂-z_1.

.

1. Работа силы тяжести положительна, если перемещение по вертикали совпадает с направлением силы.

2. На замкнутом контуре работа силы тяжести равна нулю,

3. Работа силы тяжести обратима, если в (·)2 тело освободить от внешних воздействий, то возникнет обратное движение и затраченная работа на подъем груза возвратится.

б) Работа силы трения.

Рассмотрим движение массы m со скоростью V по криволинейной траектории длиной S. Вектор скорости направлен по касательной к траектории. Сила трения F, которую будем считать постоянной, действует в противоположном направлении (рис. 12).

Рис. 12

,

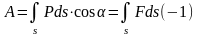1. Работа силы трения зависит от формы траектории.

2. Работа силы трения всегда отрицательна.

3. На замкнутом контуре работа силы трения не равна нулю, т.к. по мере движения перемещение непрерывно возрастает.

4. Работа силы трения необратима (Преобразуется в тепло)

в) Работа и мощность при вращении тела.

Рассмотрим твердое тело, вращающееся со скоростью W вокруг оси z (Рис.13). Приложим в произвольной точке D, находящейся на расстоянии h от оси вращения силу P, которую возложим на три взаимно перпендикулярных направлениях: параллельно оси z - P_z , по направлению нормали Р_n , по направлению касательной P_τ .

Рис. 13

При вращении тела точка D за промежуток времени dt проходит путь ds, а радиус h поворачивается на угол dφ.

Т.к. P_z и P_n перпендикулярны направлению перемещения точки D, они не могут создать работы на этом перемещении.

Таким образом, на элементарном перемещении ds работу может создать только касательная сила P_τ.. Эта работа будет равна:

.

Т.к. , можно записать , где L_z – момент силы P_τ относительно оси z.

Считая его постоянным и интегрируя в пределах положений радиуса 1-2, получим работу на конечном перемещении в виде:

.

Работа при вращении тела равна произведению вращающегося момента на угол поворота тела. Мощность при вращении тела получим как быстроту изменения работы:

.

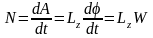3.Кинетическая энергия точки

Как было отмечено ранее, чтобы придать телу конечную скорость, необходимо не только действие силы, но и перемещение. Установим зависимость между скоростью тела и его перемещением за время действия силы.

Рассмотрим массу m, движущуюся под действием силы Р по криволинейной траектории (рис. 14). Запишем основное уравнение динамики в проекции на касательную:

.

Рис. 14

Введем в полученную зависимость перемещение, домножив обе части равенства на элементарный участок траектории ds, сопровождающий с направлением касательной в рассматриваемой точке:

.

Правая часть равенства представляет собой элементарную работу dA. В левой части равенства имеем:

и .

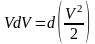Окончательно получим:

.

Величину 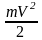называют кинетической энергией материальной точки.

Дифференциал кинетической энергии материальной точки равен элементарной работе, приложенных к ней сил.

Интегрируя полученное выражение по длине траектории, найдем:

.

Изменение кинетической энергии материальной точки за данный промежуток времени, равно работе приложенных к ней сил.

Кинетическая энергия отражает работу, которую способно совершить движущееся тело.

1. Кинетическая энергия является величиной скалярной и положительной. Следовательно, она не зависит от направления перемещения массы и характеризует движение более широко, чем векторная величина .

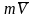2. Формула (2) является новой формой записи второго закона динамики. Здесь мерой движения является кинетическая энергия, а мерой действия силы – ее работа.

3. Кинетическая энергия оценивает движение в общем случае, даже когда оно не остается механическим, а переходит в другие виды.