3. Высота подъема ракеты.

Рассмотрим вертикальное движение одноступенчатой ракеты и определим высоту ее подъема.

В соответствии с полученным выражением для скорости ракеты запишем:

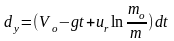
Интегрирование данного уравнения возможно только при известном режиме работы двигателя. Примем достаточно часто встречающийся на практике экспоненциальный закон сгорания топлива (рис.11):

,

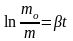
- коэффициент, зависящий от вида топлива.

Рис. 11

Подставляя в выражение для dy, и интегрируя в пределах от старта (у=0, t_o=0) до конца активного участка полета (y=y_a, t=ta), получаем:

,

.

Это формула определяет высоту подъема ракеты на активном участке полета.

Время прохода активного участка:

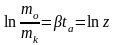, тогда .

Дальнейшее движение ракеты происходит как тела, брошенного вертикально вверх с начальной скоростью V_{max. .}

Высота свободного подъема:

.

Полная высота вертикального подъема ракеты будет:

.

Тема 8. Общие теоремы динамики точи и системы лекция № 14 общие теоремы динамики

1. Силы в механической системе

2. Центр масс

3. Теорема о движении центра масс

Литература: Парфенов Ю.М., Теплов Г.Д., Цыглин В.А. Механика, ч.1, СПБВМИ, 2006,

стр. 144 – 154.

1. Силы в механической системе.

Механической системой называется совокупность взаимодействующих масс, положение и движение которых зависит друг друга и рассматривается совместно и одновременно. Согласно этому определению любое тело можно рассматривать как систему образующих его частиц.

Рассмотрим силы, действующие в системе (рис. 1).

Будем обозначать внешние силы индексом – «е», а внутренние – «i».

Рис.1

Внешние силы в зависимости от условий, в которых находится система, могут быть не обязательно приложены ко всем массам.

Внутренние силы являются силами взаимодействия между массами системы и, следовательно, в соответствии с третьим законом Ньютона, направлены по прямой, соединяющей массы и попарно равны по модулю.

Вследствие этого главный вектор внутренних сил Rⁱ и главный момент Lⁱ будут равны нулю:

;

.

Напишем основное уравнение динамики для системы. Для отдельно взятой точки К, на которую в общем случае могут действовать и внешние и внутренние силы, будет иметь:

Суммируя по n точками системы, получаем:

,

но так как , тогда будем иметь:

.

Сумма произведений отдельных масс системы на их ускорения равна главному вектору внешних сил. Внутренние силы не влияют на движение системы в целом.

2. Центр масс.

Движение механической системы зависит как от действующих на нее сил, так и от распределения в пространстве в данный момент времени составляющих ее масс. Поэтому представляет интерес введение характеристики, учитывающей как суммарную массу системы, так и положение в ней отдельных масс. Такой характеристикой служит центр масс.

Центром масс называется геометрическая точка, характеризующая взаимное расположение всех масс системы с учетом их величины.

Центр масс – более общее понятие, чем центр тяжести, т.к. не связано с природой сил, действующих в системе. При действии на массы только сил тяжести центр масс совпадает с ее центром тяжести.

Рассмотрим систему, состоящую из n масс (рис. 2). Положение произвольной k-й массы определим радиусом вектором . Воспользуемся известным из статики выражением для определения центра тяжести.

.

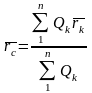Рис.2

Ввиду того, что в однородном поле тяжести вес любой частицы пропорционален ее массе, исключим вес подстановкой выражения :

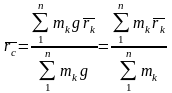
Выражение в знаменателе представляет собой массу всей системы М. Тогда будем иметь:

.

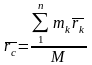В полученное равенство входят массы m_k отдельных точек системы и их радиус-векторы 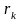. Следовательно, положение центра масс действительно характеризует распределение масс в системе.