Лекция № 13 динамика тела переменной массы

1. Уравнение Мещерского. Реактивная сила

2. Формула Циолковского для скорости ракеты

3. Высота подъема ракеты

Литература: Парфенов Ю.М., Теплов Г.Д., Цыглин В.А. Механика, ч.1, СПБВМИ, 2006,

стр. 181 – 188.

1. Уравнение Мещерского. Реактивная сила.

До настоящего времени мы рассматривали массу тела как постоянную величину. Однако в ряде случаев приходится учитывать изменение массы во времени. При движении ракеты на активном участке полета ее масса уменьшается на 60-75% за счет сгорания топлива и сброса отдельных ступеней.

Для упрощения рассмотрения будем считать движение поступательным.

Основоположником движения точки переменной массы является Мещерский, который в 1897 г. получил уравнение, явившееся теоретической базой современной теории реактивного движения.

Допущения:

1. Масса материальной точки изменяется во времени непрерывно.

2. В момент изменения массы между ней и элементарной частицей возникает силовое взаимодействие, т.е. частица не просто отделяется, а как бы отталкивается от тела, приобретая определенное количество движения.

Рассмотрим массу m, движущуюся со скоростью V, имеющую количество движения 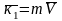. В некоторый момент времени от нее со скоростью 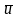отделяется элементарная частица массой dm (рис.9).

Рис. 9

Масса m при этом уменьшается, а возникающее силовое взаимодействие вызовет приращение ее скорости на величину dV. Количество движения системы может быть записано в виде:

Изменение количества движения определим разностью:

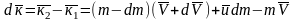
После раскрытия скобок и пренебрежения малой второго порядка , получим:

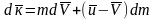
Величина 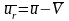является относительной скоростью отделяющихся частиц.

Тогда получим:

,

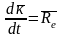; - главный вектор внешних сил.

Обозначим - реактивная сила.

Окончательно получим:

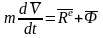- уравнение Мещерского

Его физическая сущность: изменение массы тела является причиной возникновения реактивной силы. Уравнение Мещерского – аналог основного закона динамики.

Проведем анализ этого уравнения.

1. Скорость изменения массы 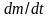называется расходом массы топлива, u_r – относительная скорость продуктов сгорания.

2. В случае отделения частиц, направление реактивной силы противоположно относительной скорости u_r .

3. Если 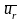↑↓ - реактивная сила движущая, ↑↑ - тормозящая.

4. Реактивная сила обращается в ноль в двух случаях:

а) u_r =0 – двигатель не работает

б) dm/dt=0 – масса не изменяется

5. Реактивная сила не зависит от скорости движения ракеты.

6. Реактивная сила может достигать величин, значительно превосходящих общий веса ракеты.

2. Формула Циолковского для скорости ракеты.

Уравнение Мещерского и независимость реактивной силы от скорости движения привели Циолковского к мысли о возможности использования реактивного двигателя для достижения космических скоростей. При реализации возникли трудности в поиске:

а) топлива, способного повысить dm/dt, т.е. сгорать быстро и в больших массах;

б) материала, способного выдержать большие давления в камере сгорания при высоких температурах, что обеспечивало увеличение относительной скорости u_r истечения продуктов сгорания.

Получим формулу Циолковского для максимальной скорости движения ракеты при следующих допущениях:

1. Ракета движется вертикально только под действием реактивной силы и собственного веса. Ускорение силы тяжести во время движения не изменяется (т.е. g=9,81 м/с² или g=0).

2. Относительная скорость истечения продуктов сгорания постоянна и направлена в сторону, противоположную движению.

Рассмотрим движение ракеты в направлении вертикальной оси у.

На старте:

V_o=0, t_o=0 m=m_к +m_т, , где m_к – масса корпуса, m_т – масса топлива.

В промежуточный момент

V, t, m V↑, t↑, m↓

В конце активного участка V_max, , t_a – время сгорания топлива, m=m_к , когда все топливо сгорает (рис. 10).

Рис. 10

Запишем уравнение Мещерского в проекции на ось y движения ракеты.

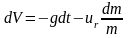
Проинтегрируем полученное уравнение в пределах от старта до промежуточного положения ракеты.

,

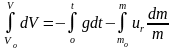
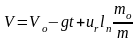
Полученная формула определяет скорость движения ракеты в любой промежуточный момент времени.

Найдем максимальную скорость в конце активного участка полета.

,

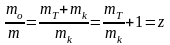z - число Циолковкого, характеризующее запас топлива. Тогда

,

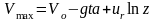t_а – зависит от закона сгорания топлива.

При движении ракеты вне сферы земного притяжения:

.

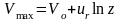Проведем анализ полученного выражения с целью оценки путей достижения больших скоростей.

1. ↑u_r – за счет рационального подбора горючего и окислителей. u_r =2÷2,5 км/с.

2. ↑z – за счет увеличения веса топлива по отношению к весу ракеты, z=3÷4.

3. Создание многоступенчатых ракет.