Лекция № 12 принцип кинетостатики (даламбера)

1. Силы инерции точки и тела

2. Момент инерции массы

3. Принцип кинетостатики

Литература: Парфенов Ю.М., Теплов Г.Д., Цыглин В.А. Механика, ч.1, СПБВМИ, 2006,

стр. 188 – 198.

1. Силы инерции точки и тела.

Сила инерции – реальная сила, приложенная к причине, вызывающей ускорение тела (по ‌‌‌‌‌‌ІІI закону Ньютона). Она зависит от массы тела и направлена противоположно ускорению.

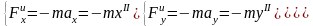
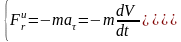
Твердое тело является совокупностью отдельных масс с постоянными расстояниями между ними. Следовательно, их силы инерции представляют собой систему, которая относительно любого центра должна производиться к главному вектору 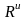и главному моменту . Выберем за центр приведения центр тяжести тела С.

а) Поступательное движение.

Рассмотрим тело массы М (рис. 4), движущееся с ускорением центра тяжести 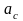. Ускорение любой точки . Тогда главный вектор сил инерции будет равен:

;

.

Рис.4

При поступательном движении тела силы инерции приводятся к равнодействующей, приложенной в его центре тяжести и равной произведению массы тела на ускорение центра тяжести.

Следовательно, масса М при поступательном движении тела полностью характеризует его инертные свойства.

б) Вращательное движение

Рассмотрим тело, вращающееся относительно оси z, проходящей через его центр тяжести с угловой скоростью и ускорением . Выделим в теле произвольную массу на расстоянии от оси вращения.

Силу инерции этой массы представим в виде трех взаимно перпендикулярных составляющих: касательной , нормальной и параллельной оси вращения .

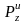Скорость массы будет направлена по касательной и равна 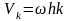(рис. 5).

Рис. 5

Главный вектор сил инерции в силу материальной симметрии тела относительно оси вращения будет равен нулю .

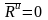Главный момент сил инерции будет создаваться только касательной силой , т.к. силы и не дают момента относительно оси вращения z.

Величина касательной силы определяется выражением:

.

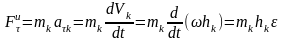Тогда главный момент сил инерции окажется равным:

.

Обозначим множитель к ускорению через 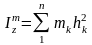, - момент инерции тела.

Тогда .

При вращении тела относительно неподвижной оси силы инерции приводятся к главному моменту, равному произведению момента инерции массы тела относительно той же оси на угловое ускорение.

2. Момент инерции массы.

Количественной характеристикой инертности тела при вращении служит момент инерции.

Он вычисляется как сумма произведений отдельных масс, составляющих тело, на квадраты их расстояний до оси вращения. Т.е. момент инерции одновременно учитывает влияние на угловое ускорение не только массы тела, но и ее распределение относительно оси вращения в зависимости от формы тела и его геометрических размеров: . Для простейших случаев (рис.6) момент инерции может быть вычислен по указанным формулам:

;

;

.

Рис. 6

3. Принцип кинетостатики.

Принцип кинетостатики обычно связывают с именем французского математика Д’Аламбера. Во многих практических случаях этот принцип облегчает и упрощает решение динамических задач по сравнению с использованием ДУ движений. Он заключается в том, что позволяет записать уравнение движения в форме уравнений равновесия, т.е. формально свести динамическую задачу к статической задаче.

Рассмотрим материальную точку массой 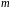, движущуюся с ускорением под действием активной силы Т и реакцией связи S. Согласно основному уравнению динамики, будем иметь следующее векторное равенство (рис.7):

.

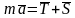Рис. 7

Перенесем произведение в правую часть равенства:

.

Выражение в скобках представляет собой силу инерции. При этом будем иметь следующее равенство:

.

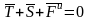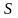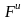Полученное выражение по форме является уравнением равновесия трех сил , и , приложенных к данному телу. Сила инерции направлена в сторону, противоположную ускорению (рис.8).

Рис. 8

Условность излагаемого приема состоит в том, что в действительности сила инерции должна быть приложена к связи, а не к движущемуся с ускорением телу.

Принцип кинетостатики может быть сформулирован следующим образом:

Уравнениям движения можно придать вид уравнений равновесия, если к реально действующим на тело активным силам и реакциям связей условно добавить силы инерции.

Для системы материальных точек принцип кинетостатики предполагает суммирование главных векторов и главных моментов соответствующих силовых факторов.