2. Дифференциальные уравнения движения точки

На рисунке 3 показана точка массой m. Траектория ее движения обозначена пунктиром. Проведем естественные оси координат – касательную 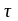и главную нормаль , - связанные с точкой, а также прямоугольную систему координат xyz в произвольной точке О пространства. Радиус-вектор r соединяет начало прямоугольной системы координат с точкой m. Скорость точки направлена по касательной к траектории, а ускорение – в сторону ее вогнутости. По второму закону динамики туда же будет направлена и действующая на точку сила.

Рис. 3

Запишем второй закон динамики, связывающий ускорение и силу, в трех известных из кинематики формах:

а) Векторная форма

Учитывая, что ускорение является второй производной по времени от радиуса-вектора, в соответствии со вторым законом динамики, получаем:

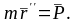
Это дифференциальное уравнение удобно для теоретических рассуждений, но сравнительно редко употребляется для решения практических задач.

б) Координатная форма

В проекциях на оси прямоугольной системы координат второй закон динамики может быть записан в виде:

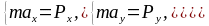
Учитывая, что проекции ускорения являются вторыми производными от соответствующих координат точки, получаем:

Эти дифференциальные уравнения удобны для практического использования в случае, когда известно положение точки на траектории.

в) Естественная форма

В проекциях на оси естественной системы координат второй закон динамики может быть записан в виде:

.

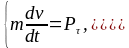
Эти уравнения удобны для практического использования в случае, когда известен закон движения точки по траектории.

3. Задачи динамики

Различают две основные задачи динамики.

а) Первая (прямая) задача

Она заключается в определении силы, вызывающей движение по заданному закону. Например, при конструировании механизмов и машин известны виды движений, которые должны совершать отдельные их элементы. Определению подлежат силы, необходимые для создания этих движений, чтобы в дальнейшем методами сопротивления материалов провести прочностные расчеты.

Другой пример: известны параметры траектории, по которой должна двигаться ракета или торпеда. Необходимо определить силы для обеспечения движения с заданными кинематическими параметрами.

Задача решается двойным дифференцированием уравнений движения.

Проиллюстрируем порядок решения прямой задачи в координатной форме. Зададим уравнения движения в параметрическом виде:

Образуя вторые производные и умножая их на массу, получим проекции силы на оси координат в виде:

Величина силы определится выражением:

а ее направление в пространстве – направляющими косинусами:

Решение первой задачи динамики не связано с математическими трудностями, т.к. заключается в простом дифференцировании, что возможно выполнить для любой функции.

б) Вторая (обратная) задача

Она заключается в определении уравнения движения по заданным силам. Например, при движении корабля, маневрировании подводной лодке или полете ракеты известны действующие на них силы. Необходимо определить параметры траектории (глубину погружения, дальность полета) и кинематические параметры движения (скорость, ускорение). Это можно выполнить только после нахождения по заданным силам уравнений движения тела.

Задача решается двойным интегрированием основного уравнения динамики.

Проиллюстрируем порядок решения обратной задачи в координатной форме. Зададим силу через ее проекции. Тогда появится возможность записать дифференциальные уравнения движения в виде:

После двойного интегрирования получим следующие выражения:

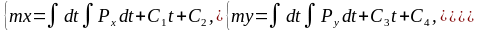
Постоянные определяются по начальным условиям, как это известно, из курса математики.

Перенося массу в правую часть равенства, окончательно будем иметь:

Решение второй задачи динамики может представить математические трудности, т.к. правая часть уравнений содержит вид функции для силы. А сила может зависеть от времени (например, сила упора гребного винта при неустановившемся движении), от расстояния (например, сила упругости) или от скорости (например, сила сопротивления воды), т.е. содержать неизвестные координаты как сами по себе, так и под знаком первой производной.

Это приводит к необходимости интегрирования системы дифференциальных уравнений, что не всегда оказывается возможным и часто требует использования приближенных методов.