Раздел 3. Динамика
Тема 7. Законы и задачи динамики. Принцип кинетостатики.
Динамика точки переменной массы
Лекция №11
Законы и задачи динамики
Законы динамики
Дифференциальные уравнения движения
Задачи динамики
Литература: Парфенов Ю.М., Теплов Г.Д., Цыглин В.А. Механика, ч.1, СПБВМИ, 2006,
стр. 136 – 144.
1.Законы динамики
Динамика изучает движение и его изменение в зависимости от действующих на тело сил. Это третий и заключительный раздел теоретической механики базируется на знаниях, полученных при изучении статики (где рассматривалось равновесие тел под действием приложенных сил) и кинематики (где рассматривалась только геометрическая сторона движения).
Законы динамики установлены на основании наблюдений за явлениями материального мира. Процессы, которые они отражают, были известны в той или иной степени в разное время различным ученым. Обобщил их, систематизировал и опубликовал И. Ньютон. Поэтому их часто называют законами Ньютона
а) Первый закон динамики
Первым законом динамики является закон инерции. Он был установлен Галилеем и обычно носит его имя.
«Под действием уравновешенной системы сил тело движется по инерции»
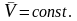
Термин «Инерция» подразумевает неизменность сохранения телом вектора скорости, т.е. его равномерное и прямолинейное движение. В частном случае тело может находиться в покое. Практика показывает: чем больше скорость тела, тем устойчивее движение, т.е. тем труднее изменить скорость тела какой-либо побудительной причиной.
Система отсчета, в которой выполняется закон инерции, называется инерциальной, а движение по отношению к ней – абсолютным. Любая система, которая движется по отношению инерциальной равномерно и прямолинейно, также является инерциальной. В этом состоит принцип относительности Галилея.
Любое криволинейное движение – это движение с ускорением. Поэтому система отсчета, связанная с Землей, принципиально не может считаться инерциальной. Только для задач, относящихся к технической практике, при ограниченных интервалах времени и расстояний, Землю можно считать условно неподвижной.
б) Второй закон динамики
Если к свободной материальной точке приложить силу, то ее движение уже не будет происходить по инерции, а она будет двигаться с ускорением. Второй закон динамики устанавливает связь между силой и ускорением.
«Ускорение пропорционально действующей силе и имеет одинаковое с ней направление».
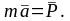
Это выражение называют основным уравнением динамики. Мерой движения здесь является ускорение, а мерой действия силы – ее величина.
На рисунке 1 показана траектория движения точки. Вектор скорости, как известно из кинематики, направлен по касательной к траектории, а вектор ускорения – в сторону ее вогнутости. По второму закону динамики вектор силы совпадает с направлением вектора ускорения. Направление движения не совпадает с направлением силы.
Рис.1
Если
сила равна нулю, то и ускорение
равно нулю. В этом случае движение
происходит по инерции с постоянной
скоростью, так как
,
следовательно
.
Таким образом, первый закон динамики
является частным случаем основного
закона.
Коэффициентом пропорциональности между ускорением и силой служит масса. Опытом установлено, что одна и та же сила вызывает различные по модулю ускорения для различных масс. Чем больше масса, тем медленнее изменяется ее скорость под действием силы, т.е. тем больше сопротивляется тело попытке вывести его из состояния инерции. Поэтому массу часто определяют как меру инертности тела – свойства сопротивляться изменению вектора скорости.
Второй закон динамики является основным для расчета движения любого отдельного тела, устанавливая количественную связь между внешним воздействием, инертными свойствами тел и возникающим при этом движении. Он дает возможность рассмотреть движение в любой момент времени и найти все его особенности.
в) Третий закон динамики
Все тела в природе воздействуют друг на друга, и это воздействие не бывает односторонним. Нельзя обнаружить случая, чтобы при действии одного тела на другое первое не испытывало бы количественно равного ответного действия.
Третий закон динамики устанавливает следующую зависимость между этими силами.
«Силы взаимодействия равны по модулю и противоположны по направлению».
Часто третий закон формулируется и как закон равенства действия и противодействия.
На рисунке 2 показаны две массы, взаимодействующие между собой. Третий закон требует равенства:
Рис. 2
Обратим внимание на то, что силы взаимодействия не составляют уравновешенную систему, так как приложены к разным телам. Если бы они уравновешивались, то никогда нельзя было бы давлением одного тела привести в движение другое.
Запишем по второму закону динамики выражения для модулей взаимодействующих сил
.
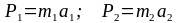По третьему закону динамики силы взаимодействия равны по модулю. Таким образом,
,
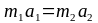откуда
Следовательно, модули ускорений, сообщаемых друг другу взаимодействующими телами, обратно пропорциональны их массам. В этом утверждении также проявляется свойство инертности тел.
Если второй закон динамики позволяет рассмотреть движение любого отдельного тела, то третий закон открывает возможность одновременно определять поведение системы взаимодействующих тел, независимо от физической природы процесса взаимодействия.