2. Скорость и ускорение при поступательном и вращательном движениях

Для абсолютного движения переменными будут все величины: координаты х, y, z, радиус-вектор и орты . Продифференцируем выражение для радиус-вектора и получим скорость абсолютного движения:

.

Таким образом, скорость точки в абсолютном движении равна геометрической сумме переносной и относительной скоростей, а ее модуль:

_.

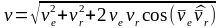Для определения ускорения точки в абсолютном движении рассмотрим два случая: при поступательном и вращательном переносном движениях.

1. При поступательном переносном движении подвижные оси координат хyz (рис.1) будут оставаться параллельными самим себе, а орты неизменными по направлению и их производные следовательно равны нулю. Тогда скорость и ускорение переносного движения будут соответственно равны:

Абсолютное ускорение, как производная от скорости, будет равно:

Итак, при поступательном переносном движении абсолютное ускорение точки является геометрической суммой переносного и относительного ускорений.

2. При вращательном переносном движении подвижная система отсчета хyz будет совершать вращение вместе с ортами и их производные не будут равны нулю:

В результате получили абсолютное ускорение как геометрическую сумму переносного и относительных ускорений, а также удвоенной суммы из произведений первых производных ординат на первые производные ортов.

Вспомним векторное выражение линейной скорости и запишем производную от вектора:

в виде векторного произведения угловой скорости на сам вектор. Это позволяет записать производные от ортов векторными произведениями угловой скорости переносного вращения на эти орты:

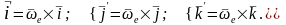
После подстановки полученных выражений в удвоенную сумму имеем:

.

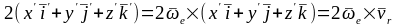Полученное двойное векторное произведение угловой скорости переносного вращения на относительную скорость точки называют поворотным ускорением или ускорением Кориолиса:

.

Ускорение Кориолиса точки равно удвоенному векторному произведению угловой скорости переносного движения ан относительную скорость точки.

Тогда абсолютное ускорение будет:

.

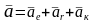Полученная формула носит название теоремы Кориолиса: при вращательном переносном движении абсолютное ускорение точки равно геометрической сумме трех ускорений: переносного, относительного и ускорения Кориолиса.

3. Ускорение Кориолиса

Рассмотрим физическую сущность и правило направления ускорения Кориолиса. Запишем абсолютное ускорение, разбив ускорение Кориолиса на два слагаемых:

Для исключения переносного и относительного ускорений рассмотрим равномерными относительное движение с v_r = const переносное вращение с = const. Пусть в момент времени t точка занимает положение 1, имеет относительную скорость v_r1, направленную по оси х, и переносную скорость v_e1, направленную перпендикулярно радиусу вращения (рис. 2).

Рис. 2

В момент времени 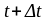точка займет положение 2 за счет перемещения по оси с v_r = const и поворота оси х на угол за счет вращения с = const. Величина относительной скорости осталась неизменной, но ее направление изменилось. В результате имеем изменение относительной скорости , вызванное переносным движением. Это изменение в пределе при и характеризует добавочное ускорение во второй скобке.

Переносная скорость при переходе из положения 1 в положение 2 изменит свою величину за счет увеличения радиуса и направление за счет поворота оси. Изменение переносной скорости в пределе обуславливает добавочное ускорение в первой скобке.

Таким образом, ускорение Кориолиса характеризует быстроту изменения относительной скорости из-за переносного вращения и быстроту изменения переносной скорости из-за относительного движения.

По правилу векторного произведения ускорение Кориолиса направлено перпендикулярно плоскости (рис.3), проходящей через векторы и , в сторону, откуда кратчайшее совмещение с наблюдается против хода часовой стрелки (правило буравчика).

Модуль векторного произведения определяется по формуле:

Рис. 3

Ускорение Кориолиса будет равно нулю в трех случаях:

1. При поступательном переносном движении = 0;

2. При отсутствии относительного движения v_r = 0;

3. При параллельности векторов и , т.е. когда угол между ними равен нулю или 180⁰.

Влиянием ускорения Кориолиса из-за вращения земли с угловой скоростью:

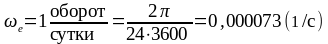
Объясняется закон Бэра о подмывании берегов рек, более значительный износ правых рельсов железных дорог в Северном полушарии, отклонение ветров и морских течений.