3. План ускорений.

План ускорений представляет собой графическое изображение векторов абсолютных ускорений точек тела в данный момент времени, отложенных из одного центра.

Рассмотрим построение плана ускорений на примере (Рис.13).

Рис. 13

Будем считать, что линейные скорости шарниров и угловые скорости вращения звеньев нам уже известны. Найдем ускорение точки А. Ввиду равномерного вращения кривошипа касательное ускорение точки А будет равно нулю. Тогда полное ее ускорение равно нормальному и определится как :

.

Оно направлено из точки А по оси кривошипа к центру его вращения О. Выберем в качестве центра плана ускорений точку и отложим из нее ускорение точки А параллельно ОА . Запишем теперь векторную формулу для определения ускорения точки В:

Ускорение точки В во вращательном движении вокруг точки А состоит из двух слагаемых – нормального и касательного. Нормальное ускорение определится по формуле:

.

Оно направлено по оси шатуна от точки В к точке А.

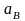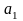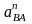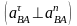На основании формулы для отложим из точки отрезок, равный ускорению и получим точку . Через построим перпендикуляр к АВ, по которому будет направлено . Ускорение ползуна В – горизонтально, поэтому построим через линию, вдоль которой будет направлено ускорение . Точка пересечения линии касательного ускорения с горизонталью и определит положение точки В.

Измеряя полученные отрезки - найдем 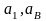, отрезок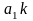 - нормальное ускорение . - касательное ускорение .

Угловое ускорение шатуна АВ может быть определено по формуле:

.

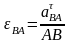Совпадение направлений и (или их противоположность) определяет ускоренный (замедленный) характер вращения.

Тема 6. Сложное движение точки лекция № 10 сложное движение точки

1. Составляющие абсолютного движения

2. Скорость и ускорение при поступательном и вращательном движении

3. Ускорение Кориолиса

Литература: Парфенов Ю.М., Теплов Г.Д., Цыглин В.А. Механика, ч.1, СПБВМИ, 2006,

стр. 125 – 135.

1. Составляющие абсолютного движения

Сложным называют движение, которое происходит одновременно в нескольких системах отсчета. Примером сложного движения может быть перемещение истребителя по палубе движущегося авианосца, движение катера по текущей реке и.т.д.

Рассмотрим сложное движение точки М (рис.1) в подвижной системе координат xyz, которая сама перемещается в пространстве относительно неподвижной системы координат x₁y₁z_1.

Рис. 1

Примем следующие определения.

1. Относительным называется движение точки в подвижной системе хyz. Ее положение характеризуется радиус-вектором:

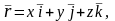
где x, y, z – координаты точки М; – орты подвижной системы координат. Скорость 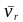и ускорение относительного движения будем обозначать индексом r.

2. Переносным называется движение подвижной системы координат хyz в неподвижной системе координат x₁y₁z_1. Ее положение будет характеризоваться радиус-вектором 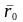и направлением ортов . Скорость и ускорение переносного движения будем обозначать индексом е.

3. Абсолютным называется движение точки в неподвижной системе x₁y₁z₁. Оно характеризуется радиус-вектором 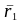и раскладывается на относительное и переносное:

Скорость v и ускорение a абсолютного движения будем обозначать без индекса.

Относительное и переносное движения будем считать независимыми. Определим кинематические параметры относительного и переносного движений.

При относительном движении точки М не учитываем движение системы хyz, т.е. считаем радиус-вектор и орты постоянными, а переменными будут только координаты х, y, z.

Для определения скорости берем производную:

откуда .

Для определения ускорения берем производную от вектора скорости:

,

откуда .

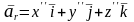При переносном движении постоянными будут координаты х, y, z, а переменными величинами будут радиус-вектор и направление ортов . С учетом этих условий:

,

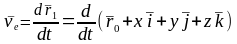имеем скорость ,

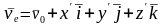а ускорение в переносном движении

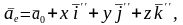
где скорость и ускорение начала подвижной системы координат (точки О).