1. Мгновенный центр скоростей.

Мгновенным центром скоростей называется точка, неизменно связанная с плоской фигурой, абсолютная скорость которой в данный момент времени равна нулю. Докажем, что такая точка существует. Приравняем выражение для скорости точки нулю:

, откуда

.

Следовательно, относительная и переносная скорости для МЦС должны быть равны по модулю и противоположны по направлению. Используя это условие, найдем положение МЦС. Рассмотрим плоскую фигуру, совершающую плоское движение со скоростью и угловой скоростью вращения вокруг полюса (Рис.11).

Рис. 11

Отложим по перпендикуляру к направлению отрезок и найдем абсолютную скорость точки Р.

.

Следовательно, абсолютная скорость точки Р в данный момент равна нулю. Эта точка и является МЦС. Если теперь точку Р принять за полюс, то для произвольной точки М получим:

.

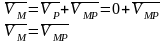Таким образом, в данный момент скорость любой точки фигуры равна ее вращательной скорости вокруг МЦС.

Т.к. было доказано, что вращательная часть движения не зависит от выбора полюса, следовательно, плоская фигура будет совершать вращение вокруг МЦС с той же угловой скоростью, с которой она поворачивается вокруг точки С.

С помощью МЦС легко определить скорость любой точки фигуры в данный момент времени. На основании теории вращательного движения эта скорость будет пропорциональна расстоянию точки от МЦС и направлена перпендикулярно отрезку, соединяющему ее с МЦС.

Для точек М и К:

; .

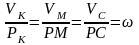
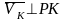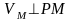Справедливо и обратное утверждение, если известны векторы скоростей двух точек тела и они не параллельны, то МЦС будет находиться на пересечении перпендикуляров к скоростям этих точек.

Итак, плоское движение можно представить не только как сочетание поступательных и вращательных движений, но и как непрерывную последовательность только поворотов вокруг МЦС, которые в разные моменты времени могут занимать разные положения на плоскости.

Следует отметить, что понятие о МЦС имеет место только для данного твердого тела, совершающего определенное движение в исследуемый момент времени.

2. План скоростей.

Решение векторных уравнений вида для нескольких точек тела, совершающего плоское движение, удобно проводить с помощью построения плана скоростей, особенно, когда нахождение скоростей с помощью МЦС затруднено ввиду его расположения за пределами чертежа. Это графоаналитический способ.

План скоростей представляет собой изображение векторов абсолютных скоростей точек тела в данный момент времени, отложенных из одного центра.

Рассмотрим простой плоский шарнирный механизм, состоящий из кривошипа ОА, вращающегося с известной угловой скоростью , шатуна АВ и ползуна В, движущегося в горизонтальных направлениях (Рис. 12).

Положение механизма определено в конкретный момент времени. Длины звеньев известны по условию. Определим скорости точек А и В, а также угловую скорость звена АВ.

Рис. 12

Скорость шарнира А определим как окружную скорость конца кривошипа в виде: .

Направлена она будет по перпендикуляру к кривошипу в сторону вращения. Для построения плана скоростей выберем произвольно центр О_V из которого в определенном масштабе отложим вектор .

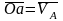Определим теперь скорость ползуна В. Ввиду того, что он может двигаться лишь горизонтально возвратно-поступательно, его скорость будет горизонтальна. Проведем из центра плана пунктирную линию по направлению скорости 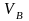. Величина пока остается неизвестной.

Воспользуемся известной векторной формулой:

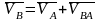
Вращательная скорость 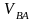должна быть перпендикулярна шатуну АВ, т.к. это скорость точки В при вращении звена АВ вокруг точки В при вращении звена АВ вокруг точки А. По правилу сложения векторов проведем через точку 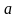(конец вектора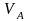 ) линию, перпендикулярную шатуну АВ, которая будет линией направления вращательной скорости . Точка пересечения этой линии с линией скорости , проходящей через центр плана определит положение точки . Соединяя центр плана с точкой , получаем вектор скорости . Измеряя его длину и учитывая выбранный масштаб, получим численное значение скорости .

План скоростей позволяет графически определить скорость любой точки механизма. Следует помнить, что отрезок, соединяющий концы векторов абсолютных скоростей точек тела на плане скоростей, перпендикулярен отрезку, соединяющему соответствующие точки тела, и пропорционален ему. 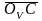Так для определения скорости точки С, расположенной посередине шатуна АВ, надо на плане скоростей разделить точкой С пополам отрезок и провести вектор из центра плана. Измеряя длину этого вектора и учитывая масштаб, можно получить значение .

Угловую скорость шатуна найдем по формуле:

.
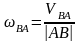