2. Скорости при плоском движении.

Рассмотрим движение плоской фигуры. Если известны уравнения движения, то скорость поступательного движения фигуры, равная скорости полюса С, определиться выражением:

.

Скорость вращательного движения вокруг полюса, не зависящая от его выбора, будет равна:

.

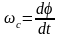Будем считать и 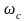заданными. Определим скорость произвольной точки М, расположенной на расстоянии СМ от полюса (Рис. 8). Она совершает сложное движение.

Рис. 8

Полагая поступательное движение плоской фигуры переносным, а вращательное относительным, на основании теории о сложении скоростей, будем иметь следующую векторную формулу для скорости произвольной точки:

.

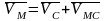где - скорость точки М в поступательном движении, по величине и направлению равная скорости полюса, - скорость точки М во вращательном движении вокруг полюса С. Вектор этой скорости направлен в сторону вращения под прямым углом к линии, соединяющей точку М с полюсом С.

При этом, на основании теории вращательного движения, будут справедливы следующие соотношения:

; .

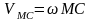Таким образом, скорость произвольной точки тела, совершающего плоское движение, является геометрической суммой скоростей, которые она получает в поступательном движении вместе с полюсом и во вращательном движении вокруг полюса.

Модуль скорости может быть определен по известной формуле для векторной суммы:

.

Докажем важную для практики теорему: «Проекции скоростей двух точек тела на прямую, соединяющую эти точки равны между собой».

Рис. 9

Спроецируем векторное равенство 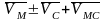на прямую, проходящую через точки С и М (Рис. 9).

.

.

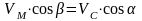Из теоремы следует, что нельзя задавать произвольно по модулю и направлению скорости двух точек абсолютно твердого тела.

3. Векторная формула ускорения при плоском движении.

Рассмотрим движение плоской фигуры как сочетание поступательного движения вместе с полюсом С и вращательного вокруг этого полюса. Определим ускорение произвольной точки М, расположенной на расстоянии СМ от полюса (Рис. 10).

Рис. 10

Полагая поступательное движение переносным, а вращательное – относительным, на основании теоремы о сложении ускорений, будем иметь:

.

где 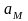- абсолютное ускорение произвольной точки М;

- ускорение точки М в поступательном движении, по величине и направлению, равное ускорению полюса С;

- ускорение точки М во вращательном движении вокруг полюса С.

.

где - нормальное ускорение, вектор которого всегда направлен от точки М по радиусу к центру вращения (к полюсу С). Оно может быть вычислено по известной формуле:

,

- касательное ускорение, вектор которого направлен перпендикулярно радиусу СМ. При ускоренном вращении он совпадает по направлению с вектором относительной скорости , а при замедленном – противоположен.

.

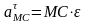Таким образом:

.

ЛЕКЦИЯ № 9

Методы исследования плоскопараллельного движения твердого тела

1. Мгновенный центр скоростей (МЦС)

2. План скоростей

3. План ускорений

Литература: Парфенов Ю.М., Теплов Г.Д., Цыглин В.А. Механика, ч.1, СПБВМИ, 2006,

стр. 111 – 124.